从数据到结论(人民大学吴喜之教授)09判别分析.ppt

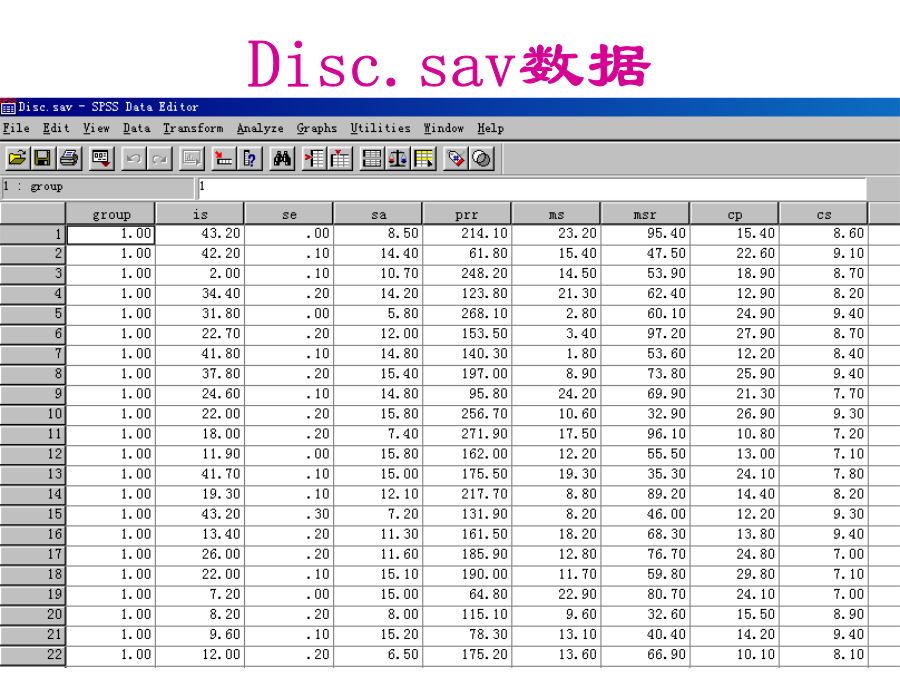
判别分析判别判别分析(discriminantanalysis)判别分析例子Disc.sav数据根据距离的判别（不用投影）Fisher判别法(先进行投影)逐步判别法(仅仅是在前面的方法中加入变量选择的功能)Disc.sav例子Disc.sav例子Disc.sav例子Disc.sav例子Disc.sav例子误判和正确判别率Disc.sav例子Disc.sav例子判别分析要注意什么？判别分析要注意什么？SPSS选项判别分析(DiscriminantAnalysis)和聚类分析的关系距离判别法Mahalanobis距离线性判别函数:当S(1)=S(2)=S时当m(1),m(2),S已知时,
令a=S-1(m(1)-m(2))≡(a1,…,ap)’,则当m(1),m(2),S未知时,
可通过样本来估计:非线性判别函数:当S(1)≠S(2)时多总体时的线性判别函数:当S(1)=…=S(k)=S时非线性判别函数:当S(1),…,S(k)不等时费歇(Fisher)判别法将Gm组中数据投影的均值记为有组间离差平方和为:注:L=|E|/|B+E|为有Wilks分布的检验零假设H0:m(1)=…=m(k)的似然比统计量.Wilks分布常用c2分布近似(Bartlett)希望寻找a使得SSG尽可能大而SSE尽可能小,即m个判别函数的判别能力定义为总体方差不等时,注意到的样本方差为用m个线性判别函数yi(x)=vi’x,i=1,…,m,时,先将样本点在L(vi,…,vm)空间投影再按照p>1情况的距离判别法来制定判别规则.判别能力为m=1时,不加权法:m>1时,不加权法:记
对x=(x1,…,)’,yl(x)=v(l)’xBayes判别法逐步判别法鸢尾花数据(花瓣,花萼的长宽)5个变量:花瓣长(slen),花瓣宽(swid),花萼长(plen),花萼宽(pwid),分类号(1:Setosa,2:Versicolor,3:Virginica)(data14-04)Statistics→Classify→Discriminant:
Variables:independent(slen,swid,plen,pwid)Grouping(spno)Definerange(min-1,max-3)
Classify:priorprobability(Allgroupequal)usecovariancematrix(Within-groups)Plots(Combined-groups,Separate-groups,Territorialmap)Display(Summarytable)
Statistics:Descriptive(Means)FunctionCoefficients(Fisher’s,Unstandardized)Matrix(Within-groupscorrelation,Within-groupscovariance,Separate-groupscovariance,Totalcovariance)
Save:(Predictedgroupmembership,DiscriminantScores,Probabilityofgroupmembership)鸢尾花数据(数据分析过程简明表)鸢尾花数据(原始数据的描述)鸢尾花数据(合并类内相关阵和协方差阵)鸢尾花数据(总协方差阵)鸢尾花数据(特征值表)Eigenvalue:用于分析的前两个典则判别函数的特征值,是组间平方和与组内平方和之比值.最大特征值与组均值最大的向量对应,第二大特征值对应着次大的组均值向量典则相关系数(canonicalcorrelation):是组间平方和与总平方和之比的平方根.被平方的是由组间差异解释的变异总和的比.鸢尾花数据(Wilks’Lambda统计量)检验的零假设是各组变量均值相等.Lambda接近0表示组均值不同,接近1表示组均值没有不同.Chi-square是lambda的卡方转换,用于确定其显著性.鸢尾花数据(有关判别函数的输出)鸢尾花数据(有关判别函数的输出)鸢尾花数据(有关判别函数的输出)这是类均值(重心)处的典则判别函数值鸢尾花数据(用判别函数对观测量分类结果)TerritorialMap
CanonicalDiscriminant
Function2
-12.0-8.0-4.0.04.08.012.0
趄蝌蝌蝌蝌趄蝌蝌蝌蝌趄蝌蝌蝌蝌趄蝌蝌蝌蝌趄蝌蝌蝌蝌趄蝌蝌蝌蝌
12.01223
1223
1223
1223
1223
1223
8.01223
1223
1223
1223
1223
1223
4.01223
1223
1223
1223
1223
1223*
.0*1223
12*23
1223
1223
1223
1223
-4.0122