
矩阵光学方法在谐振腔理论中的应用.pdf

as****16





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

矩阵光学方法在谐振腔理论中的应用.pdf
《激光杂志》89年第如誊第6期^SER30URNAL(VoI.10,N}6,1989)矩阵光学方法在谐振腔理论中的应用吕百达(四】ll大学物理系)挺要:本文使用矩阵光学方法,对稳定腔和非稳腔的基模特征作了分析和讨论。Applicationofmatrixopticsmethodsinresonatortheory三nBalda(DepartmentofPhysics,SichuanUniversity)Abstract:InthispaperJthecharacteristicsoffundamental
激光原理光学谐振腔理论ABCD矩阵.pptx
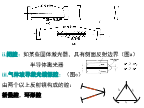
ii.闭腔:如某些固体激光器,具有侧面反射边界(图a)半导体激光器iii.气体波导激光谐振腔:(图c)由两个以上反射镜构成的腔:折叠腔,环形腔开腔内插入透镜一类光学元件——复合腔分布反馈式谐振腔:(DistributedFeedback,DFB)二、腔的模式腔的模式:光学谐振腔内可能存在的电磁场的本征态谐振腔所约束的一定空间内存在的电磁场,只能存在于一系列分立的本征态腔内电磁场的本征态因此:腔的具体结构腔内可能存在的模式(电磁场本征态)模的基本特征主要包括:1、每一个模的电磁场分布E(x,y,z),腔的横
激光原理光学谐振腔理论ABCD矩阵.pptx
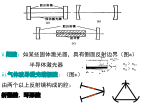
ii.闭腔:如某些固体激光器,具有侧面反射边界(图a)半导体激光器iii.气体波导激光谐振腔:(图c)由两个以上反射镜构成的腔:折叠腔,环形腔开腔内插入透镜一类光学元件——复合腔分布反馈式谐振腔:(DistributedFeedback,DFB)二、腔的模式腔的模式:光学谐振腔内可能存在的电磁场的本征态谐振腔所约束的一定空间内存在的电磁场,只能存在于一系列分立的本征态腔内电磁场的本征态因此:腔的具体结构腔内可能存在的模式(电磁场本征态)模的基本特征主要包括:1、每一个模的电磁场分布E(x,y,z),腔的横

矩阵理论在细分方法中的应用.doc
附录矩阵理论在细分方法中的应用线性代数理论对计算技术的提高具有非凡的指导意义.本章仅就几何造型细分方法中矩阵与特征值的应用做浅显的介绍.设给定8个初始控制顶点,将它们按序连接成如图1(a)所示的初始闭凸八边形,接下来的目的是要生成与初始闭凸八边形形状尺度相近的光滑闭曲线,这其中矩阵乘积起到至关重要的作用.1.细分算法将初始控制多边形定义为第0层,即,将一定的细分规则作用于初始控制多边形上,产生第1层控制顶点,此时的控制顶点数一般是第0层控制顶点数的2倍,按照一定的连接规则连接这些控制顶点形成第1层控制多边

矩阵理论在细分方法中的应用.doc
矩阵理论在细分方法中的应用(完整版)实用资料(可以直接使用,可编辑完整版实用资料,欢迎下载)附录矩阵理论在细分方法中的应用线性代数理论对计算技术的提高具有非凡的指导意义.本章仅就几何造型细分方法中矩阵与特征值的应用做浅显的介绍.设给定8个初始控制顶点,将它们按序连接成如图1(a)所示的初始闭凸八边形,接下来的目的是要生成与初始闭凸八边形形状尺度相近的光滑闭曲线,这其中矩阵乘积起到至关重要的作用.1.细分算法将初始控制多边形定义为第0层,即,将一定的细分规则作用于初始控制多边形上,产生第1层控制顶点,此时的
