
概率论与数理统计第9讲.ppt

qw****27




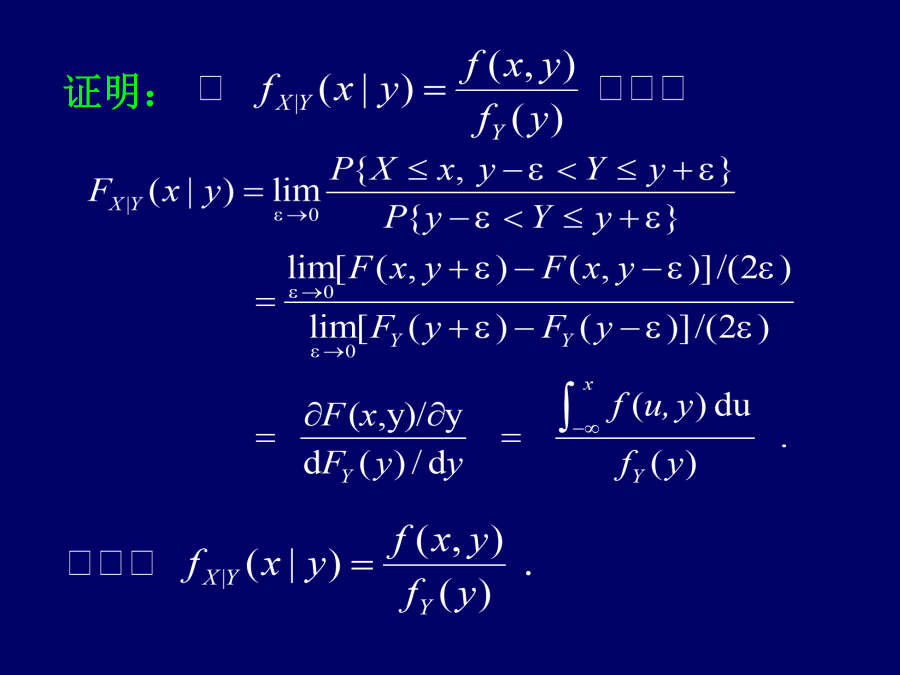





亲,该文档总共33页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

概率论与数理统计第9讲.ppt
概率论与数理统计第九讲3.5.3连续型随机变量的条件概率密度定义2:设X和Y是随机变量,给定y,若对任意固定正数ε,P(y-ε<Y≤y+ε)>0,且对任意实数x,极限同理,当fX(x)>0时,证明:例3:设(X,Y)服从单位圆上均匀分布,即其概率密度为当|x|<1时,有求P(X>1|Y=y)。由于故对y>0,解:概率密度不为零的区域如右图所示。当y(0,1]时,fY(y)>0,当x(-1,1)时,fX(x)>0,例6:设店主在每日开门营业时,放在柜台上的货物量为Y,当日销售量为X,假定一天中不再往柜台

概率论与数理统计第9讲.ppt
概率论与数理统计第9讲2因此算出X的分布律为二,常用连续型分布1.均匀分布定义2若连续型随机变量X的概率密度为注:在区间(a,b)上服从均匀分布的随机变量X,其取值落在(a,b)中任意等长度的子区间的概率是相同的,且与子区间的长度成正比.事件上,任取子区间(c,c+l)(a,b),由上节例1求得X的分布函数F(x)与f(x)的图形对照如下:例5某公共汽车站从上午7时起,每15分钟来一班车,即7:00,7:15,7:30,7:45等时刻有汽车到达此站.如果乘客到达此站时间X是7:00到7:30之间的均匀随

概率论与数理统计第7讲.pptx
一、分布函数的定义由分布函数的定义对任意实数x随机变量落在任意点x内的概率为:说明证明所以即任一分布函数处处右连续.反过来如果一个函数具有上述性质则一定是某个r.vX的分布函数.也就是说性质(1)--(4)是鉴别一个函数是否是某r.v的分布函数的充分必要条件.三、离散型随机变量X的分布函数四、用分布函数计算某些事件的概率例1:设随机变量X的分布律为:求X的分布函数.x说明:例2:设随机变量X的分布函数为例3设随机变量X的分布函数

概率论与数理统计第3讲.ppt
我们首先引入的计算概率的数学模型,是在概率论的发展过程中最早出现的研究对象,通常称为一、古典概型常常把这样的试验结果称为“等可能的”.2因为抽取时这些球是完全平等的,我们没有理由认为10个球中的某一个会比另一个更容易取得.也就是说,10个球中的任一个被取出的机会是相等的,均为1/10.我们用i表示取到i号球,i=1,2,…,10.称这种试验为有穷等可能随机试验或古典概型.二、古典概型中事件概率的计算这里实际上是从“比例”转化为“概率”请回答:基本计数原理例如,某人要从甲地到乙地去,基本计数原理例如,若一个

概率论与数理统计第15讲.ppt
一、随机变量方差的概念及性质由第一节知道,随机变量的数学期望可以反映随机变量取值的平均程度,但仅用数学期望描述一个随机变量的取值情况是远远不够的。容易算得,甲乙两种牌号的手表的数学期望都是0秒,现问,甲乙两种牌号的手表哪一种更准确?任给随机变量X,EX是其数学期望,显然,|X-EX|反映了偏离的大小,由于绝对值有诸多不便,所以用(X-EX)2去衡量这个偏差,从而(X-EX)2仍为随机变量,所以用(X-EX)2的平均值去衡量离开它的平均值EX的偏离程度,引入定义:1.方差的定义(1)由定义知,方差是r.v.
