
实验三 参数估计与假设检验.doc

kp****93








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

实验三 参数估计与假设检验.doc
实验三参数估计与假设检验实验四(1)CONFIDENCE函数求置信区间公式:CONFIDENCE(显著水平Alpha,数据区域的总体标准偏差假设为已知Standard_dev,样本容量size)实验内容及步骤利用“描述统计”分析工具,可以计算正态分布下方差未知的样本均值极限误差,从而实现单个正态总体均值的区间估计。直接调用函数CONFIDENCE,输入参数值计算置信区间。在Excel中直接输入命令CONFIDENCE和相应参数计算置信区间。实验四(2)总体方差已知均值的假设检验实验目的及要求掌握利用Exc

实验三 用EXCEL进行参数估计和假设检验.docx
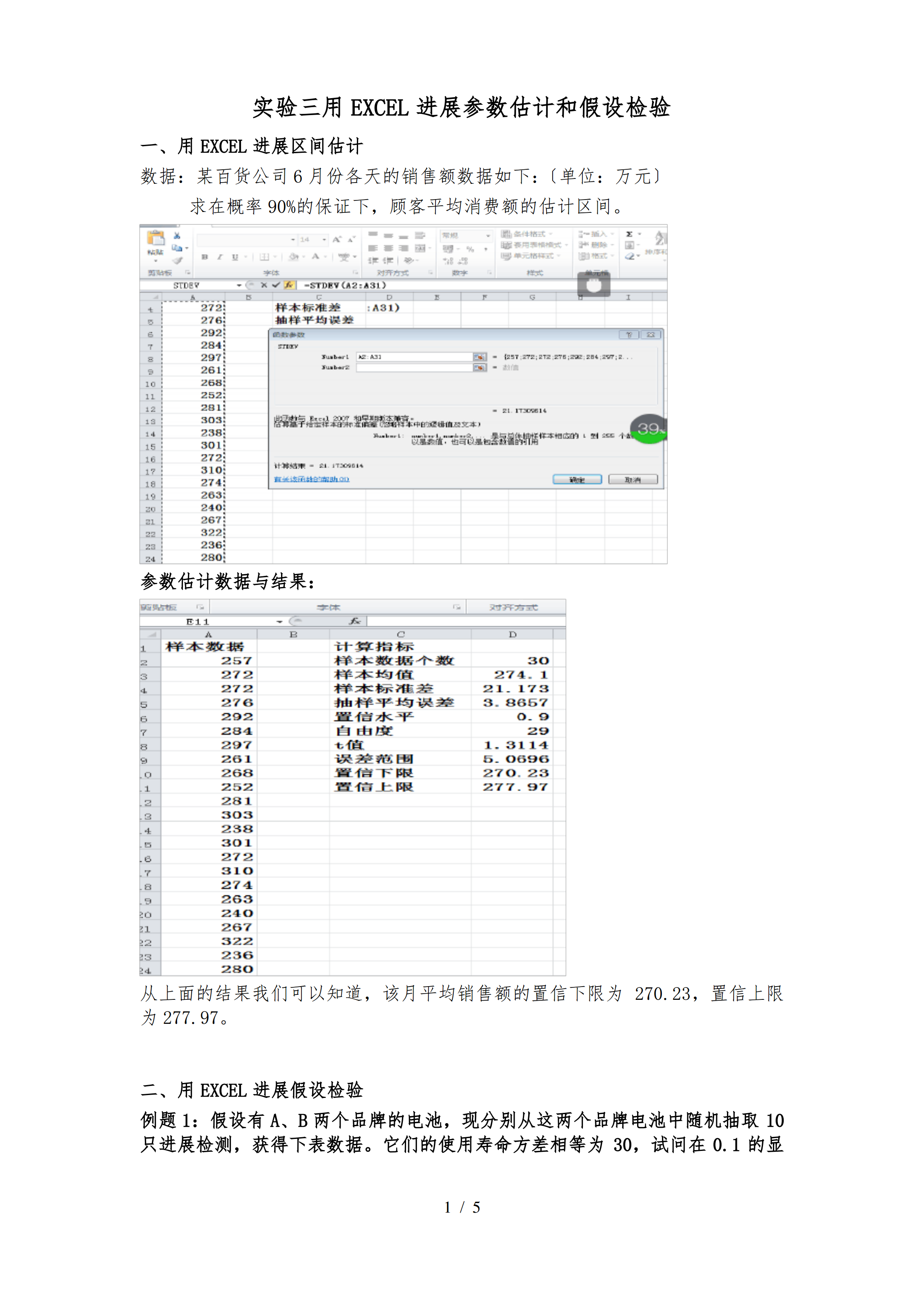
实验三用EXCEL进行参数估计和假设检验一、用EXCEL进行区间估计数据:某百货公司6月份各天的销售额数据如下:(单位:万元)求在概率90%的保证下,顾客平均消费额的估计区间。参数估计数据及结果:从上面的结果我们可以知道,该月平均销售额的置信下限为270.23,置信上限为277.97。二、用EXCEL进行假设检验例题1:假设有A、B两个品牌的电池,现分别从这两个品牌电池中随机抽取10只进行检测,获得下表数据。它们的使用寿命方差相等为30,试问在0.1的显著性水平下,可否认为两个品牌的平均使用寿命存在显著差
实验三-用EXCEL进行参数估计和假设检验.pdf
实验三用EXCEL进展参数估计和假设检验一、用EXCEL进展区间估计数据:某百货公司6月份各天的销售额数据如下:〔单位:万元〕求在概率90%的保证下顾客平均消费额的估计区间。参数估计数据与结果:从上面的结果我们可以知道该月平均销售额的置信下限为270.23置信上限为277.97。二、用EXCEL进展假设检验例题1:假设有A、B两个品牌的电池现分别从这两个品牌电池

抽样分布、参数估计及假设检验实验.doc
实验类别:综合性专业:数学与应用数学中北大学理学院实验二、抽样分布、参数估计及假设检验实验【实验内容】1、培养学生建立概率统计模型的能力2、熟悉用数理统计中常用的Matlab命令格式、程序及运行结果3、学会用Matlab统计箱来完成数据统计描述和分析方法4、给出100名学生的身高和体重(单位厘米千克)①求出以下统计量:样本矩(moment),平均值(mean),中位数(median),样本标准差(std),最大值(max),最小值(min),极差(range)。②求出频率与频数分布;③作出以上数据的频率直

参数估计与假设检验.doc
参数估计与假设检验参数估计与假设检验参数估计与假设检验参数估计与假设检验一、实验目的1、掌握正态总体和大样本下总体的参数估计和假设检验的方法;2、了解其他参数估计和假设检验的大致操作步骤;2、重点掌握单个总体均值的检验方法、掌握应用Excel计算P值的步骤.二、实验内容某机床厂加工一种零件,根据经验知道,该厂加工零件的椭圆度服从正态分布,其总体均值为0.081mm,今换一种新机床进行加工,取200个零件进行检验,得到椭圆度的均值为0。076mm,样本标准差为0.025mm,问新机床加工零件的椭圆度总体均值
