曲线积分与曲面积分-豆柴文库

曲线积分与曲面积分.ppt

2024-08-19

10金币

461KB

25页

kp****93

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

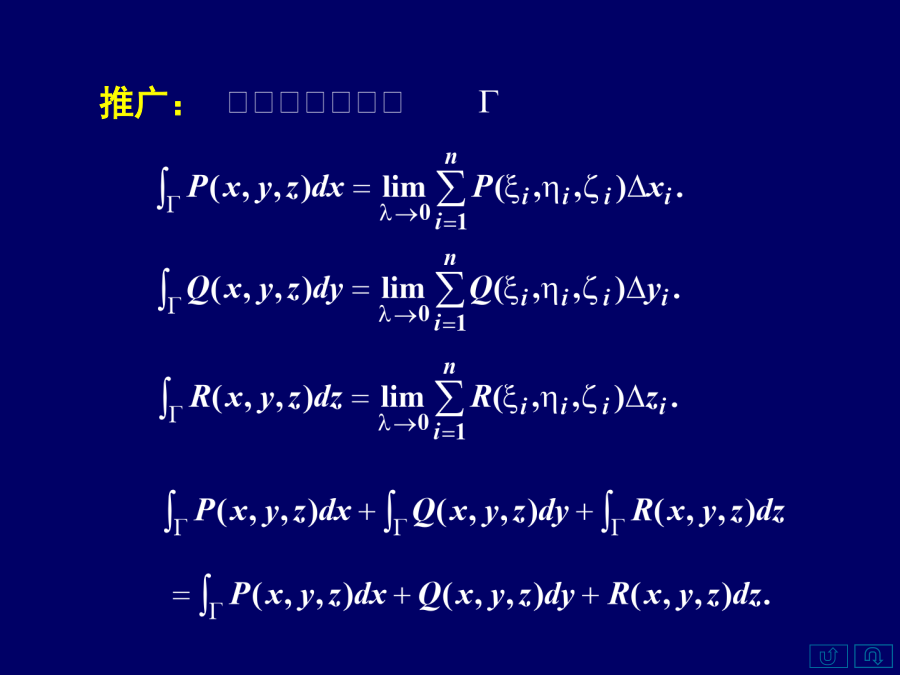
亲，该文档总共25页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

曲面曲线积分.docx

第十章曲线积分与曲面积分一、教学目标及基本要求：1、理解二类曲线积分的概念，了解两类曲线积分的性质及两类曲线积分的关系。2、会计算两类曲线积分3、掌握（Green）公式，会使用平面曲线积分与路径无关的条件。4、了解两类曲面积分的概念及高斯（Grass）公式和斯托克斯（Stokes）公式并会计算两类曲面积分。5、了解通量，散度，旋度的概念及其计算方法。6、会用曲线积分及曲面积分求一些几何量与物理量（如曲面面积、弧长、质量、重心、转动惯量、功、流量等）。二、教学内容及学时分配：第一节对弧长的曲线积分2学时第二

2024-11-05

68KB

曲线积分与曲面积分.doc

第十章曲线积分与曲面积分基本内容要求理解线、面积分的概念，了解线、面积分的几何意义及物理意义，能用线、面积分表达一些几何量和物理量；掌握线、面积分的计算法；知道两类曲线积分及两类曲面积分的联系；掌握格林公式，并能将沿闭曲线正向的积分化为该曲线所围闭区域上的二重积分；掌握曲线积分与路径无关的充要条件，并能求全微分为已知的某个原函数，注意此时所讨论问题单连通域的条件不可缺少；掌握高斯公式，并能将闭曲面Σ外侧上的一个曲面积分化为由其所围空间闭区间Ω上的三重积分。选择1．设是从O（0，0）到点M（1，1）的直线段

2024-08-19

323KB

曲线积分与曲面积分.ppt

第二节对坐标的曲线积分一、对坐标的曲线积分的概念分割定义类似地定义推广：性质二、对坐标的曲线积分的计算曲线特殊情形对坐标的曲线积分的计算公式例1解2：例2被积函数相同，起点和终点也相同，但路径不同积分结果不同.例3被积函数相同，起点和终点也相同，虽然路径不同，但积分结果相同.例4三、两类曲线积分之间的联系---两类曲线积分之间的联系例5可用向量表示四、小结

2024-08-19

461KB

曲线积分与曲面积分.docx

第十一章曲线积分与曲面积分教学目的：理解两类曲线积分的概念，了解两类曲线积分的性质及两类曲线积分的关系。掌握计算两类曲线积分的方法。熟练掌握格林公式并会运用平面曲线积分与路径无关的条件，会求全微分的原函数。了解两类曲面积分的概念、性质及两类曲面积分的关系，掌握计算两类曲面积分的方法，了解高斯公式、斯托克斯公式，会用高斯公式计算曲面积分。知道散度与旋度的概念，并会计算。会用曲线积分及曲面积分求一些几何量与物理量。教学重点:两类曲线积分的计算方法；格林公式及其应用；两类曲面积分的计算方法；高斯公式、斯托克斯公

2024-11-08

308KB

曲线积分与曲面积分.docx

第十章曲线积分与曲面积分10.01填空(1)第二类曲线积分化成第一类曲线积分是，其中﹑﹑为上点处切向量的方向角。(2)第二类曲面积分化成第一类曲面积分是，其中﹑﹑为上点处的法向量的方向角10.02计算下列曲线积分：x2+y2=ax0axya/2Lθ(1),其中为圆周解：表示为参数方程:有(2),其中为曲线，，，解：(3),其中为摆线，上对应从到的一段弧。解:(4)，其中是曲线上由到的一段弧。解:（5），其中L为上半圆周，沿逆时针方向。解:补直线段由格林公式,有Dyx02aa(x-a)2+y2=a2LA区域

2024-11-06

129KB