内容提供者
双曲线 (2).doc
2024-08-17
10金币
89KB
2页
dc****76
实名认证
内容提供者
1/2
2/2
在线预览结束，喜欢就下载吧，查找使用更方便
相关资料
双曲线 (2).doc
1.双曲线的中心在原点，关于坐标轴对称，一条渐近线方程为，则双曲线的离心率等于已知双曲线的方程为，则过点P(0，10)与双曲线只有一个公共点的直线方程为已知双曲线C：的左右焦点分别为,点P在双曲线C上，,则等于已知F是双曲线的左焦点，A（1,4），P是双曲线右支上的动点，则在双曲线上求一点M，使它到直线的距离最短，并求最短距离.已知直线与双曲线的左支交于A,B两点，若另有一条直线经过P(-2，0)及线段AB的中点Q.求的取值范围；求直线在轴上的截距的取值范围.已知直线与双曲线有A,B两个不同的交点.如果以
2024-08-17
10
89KB
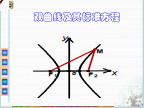
双曲线方程2.ppt
1.椭圆的定义①如图(A)，①两个定点F1、F2——双曲线的焦点;1.建系设点.F问题：如何判断双曲线的焦点在哪个轴上？例1已知双曲线的焦点为F1(-5,0),F2(5,0)，双曲线上一点P到F1、F2的距离的差的绝对值等于6，求双曲线的标准方程.练习1:如果方程表示双曲线，求m的取值范围.练习2:证明椭圆与双曲线例2、双曲线的两个焦点为F1、F2，点P在双曲线上，若PF1⊥PF2，则点P到x轴的距离为_________练习：设F1、F2是双曲线的两个焦点，点P在双曲线上，若∠F1PF2=90o，则△F1
2024-08-16
10
1KB
直线与双曲线(2).ppt
双曲线与直线的位置关系复习与提高问题一：课本引入双曲线的渐近线概念有何用意呢？渐近线本身有何特点？问题二：如何由双曲线方程写出其渐近线方程呢？问题三：如何由已知渐近线方程写出对应的双曲线方程呢？由我们解过的题可知：1、渐近线方程确定且过一个定点的双曲线方程只有一解，而渐近线方程确定且已知a（实半轴长）、b（虚半轴长）、c（半焦距）三者之一的双曲线方程则有两解；2、使用共渐近线的双曲线系思想来解已知渐近线求双曲线方程的题型，可使思路清晰，讨论目的明确。思考1：双曲线与直线有什么样的位置关系？思考2：怎样判断
2024-06-27
10
781KB
双曲线教案 (2).doc
课题双曲线及其标准方程教师毛锡平教学目标知识目标：使学生掌握双曲线的定义，理解双曲线标准方程的推导，能根据条件确定双曲线的标准方程能力目标：培养学生类比分析，归纳总结的能力和用运动变化的观点去研究问题的能力。德育目标：培养学生积极思考，勇于探索的精神教学重点双曲线的定义及其标准方程（解决办法：通过演示得出双曲线，再设问给出定义，通过比较加深理解）教学难点双曲线标准方程的推导（解决办法：引导学生与椭圆标准方程推导类比）教学疑点双曲线定义中“距离的差的绝对值为常数”的“绝对值”的理解（解决办法：分析定义中常数
2024-08-17
10
43KB
2、双曲线的参数方程 (2).ppt
二、圆锥曲线的参数方程•双曲线的参数方程例2、
2024-06-11
10
193KB