预览加载中，请您耐心等待几秒...

数值分析4Newton迭代法.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共18页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

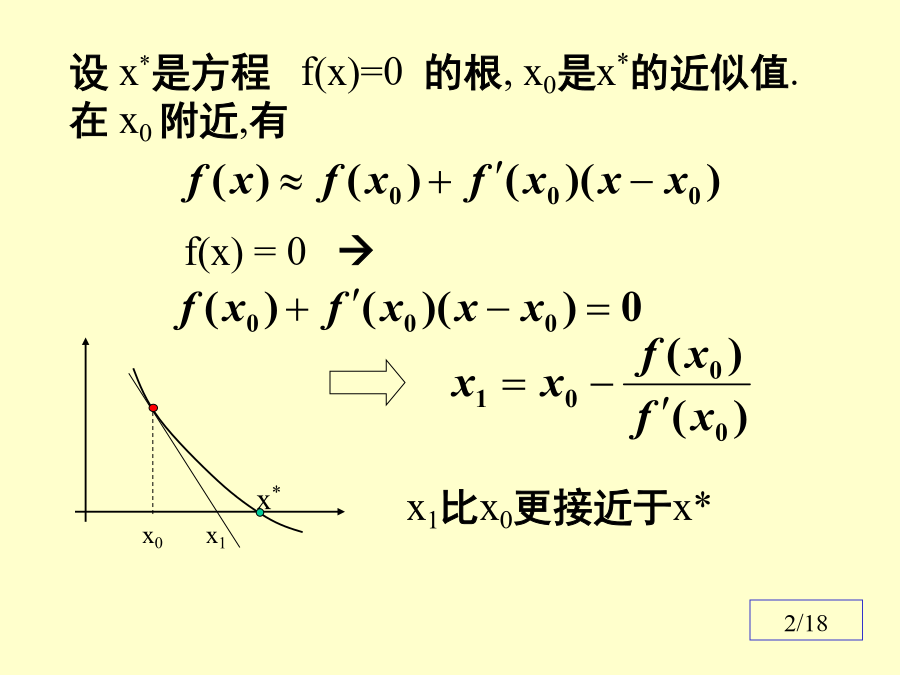
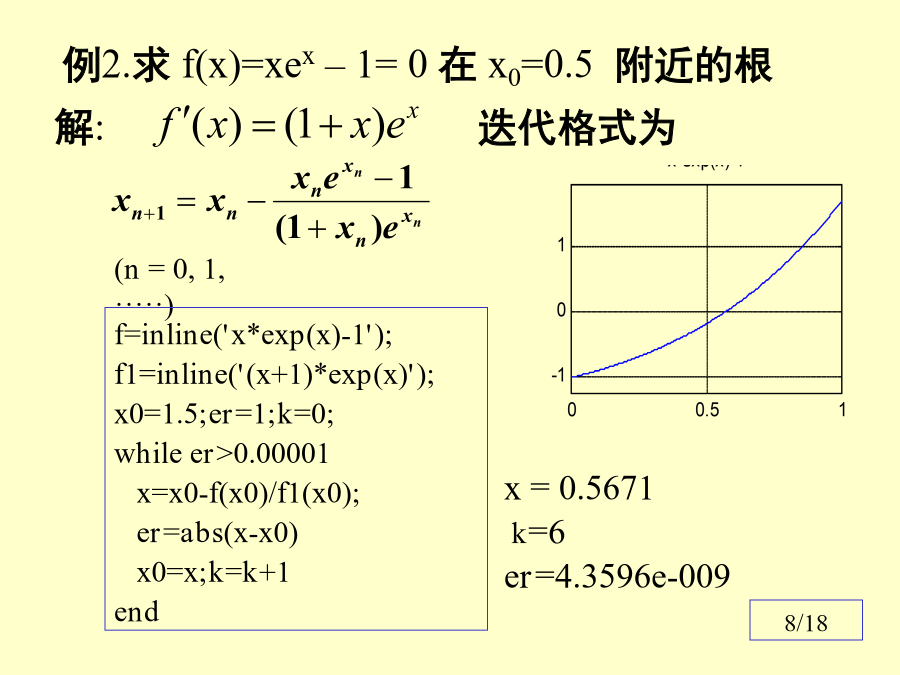
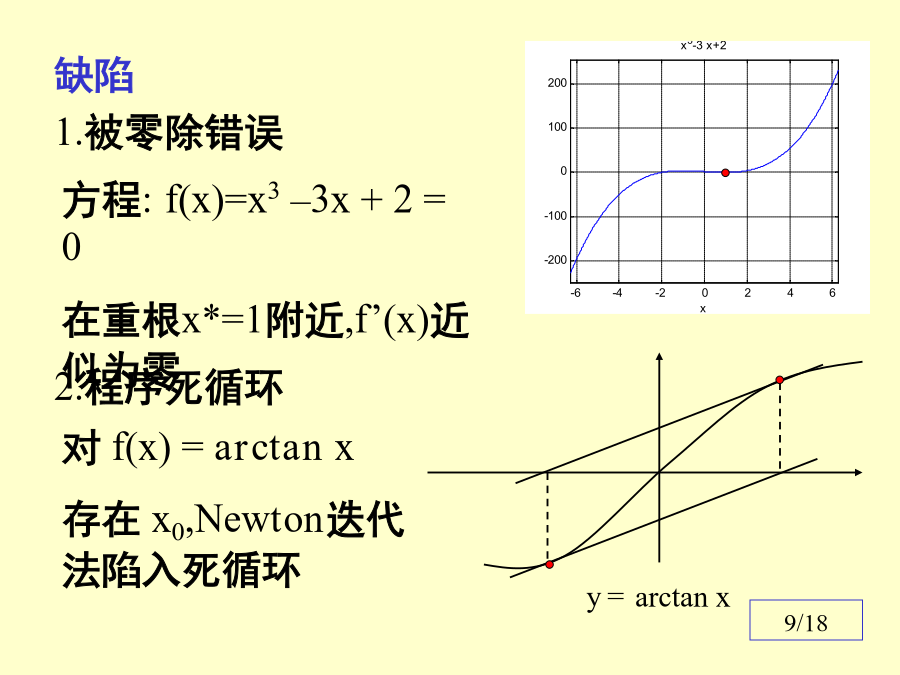
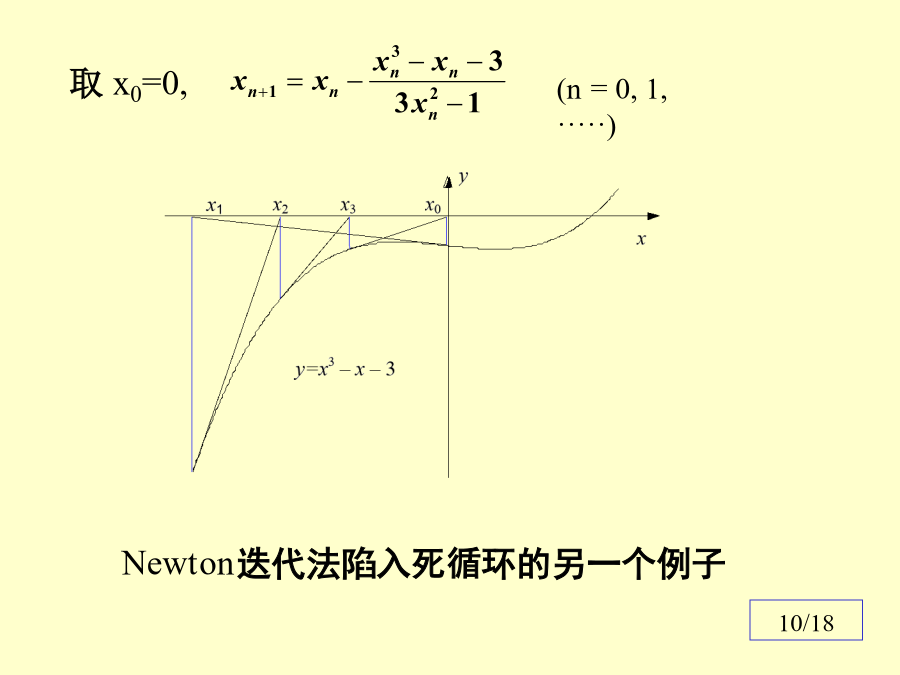
《数值分析》4设x*是方程f(x)=0的根,x0是x*的近似值.在x0附近,有(n=0,1,2,·····)例1平方根算法(n=0,1,·····) 的收敛性证明及收敛阶估计.(n=0,1,·····)由此可知,平方根迭代是2阶收敛.Newton迭代法的局部收敛性例2.求f(x)=xex–1=0在x0=0.5附近的根缺陷Newton迭代法陷入死循环的另一个例子f’<0,f”>0定理:若函数f(x)在[a，b]上满足条件13/18设x*是方程f(x)=0的根,x0和x1是x*附近的两个点.(n=1,2,·······)f=inline(‘u.*cosh(50/u)-u-10'); a0=120;a=150;k=1; y0=f(a0);y=f(a); whileabs(a0-a)>0.0001 t=a-y*(a-a0)/(y-y0); a0=a;y0=y; a=t;y=f(a); k=k+1; end牛顿迭代法的收敛域问题: 用牛顿迭代法求解复数方程z3–1=0，该方程在复平面上三个根分别是