
第七章数学解题的思维过程.ppt

kp****93





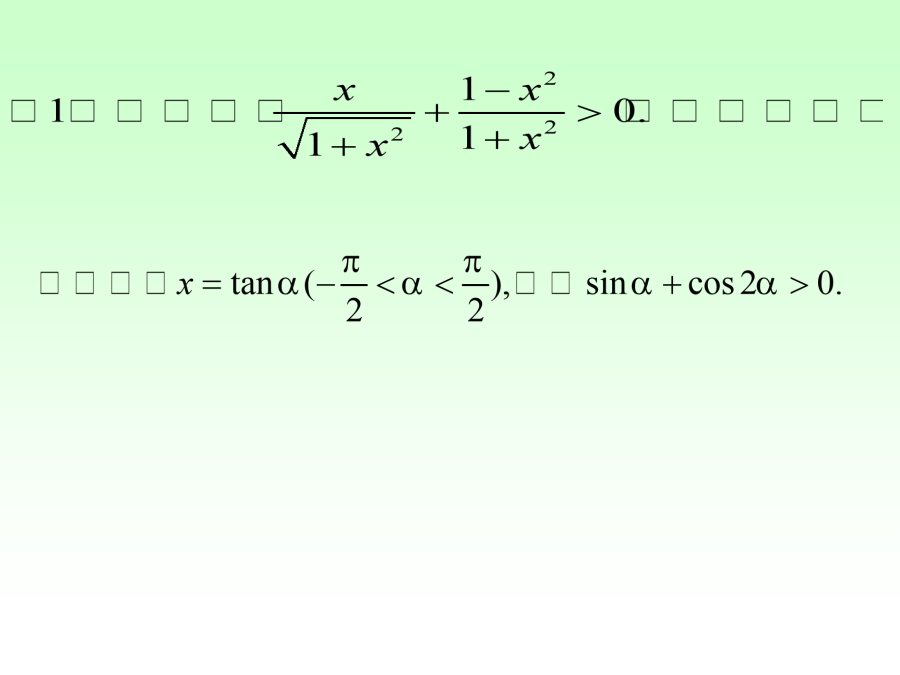
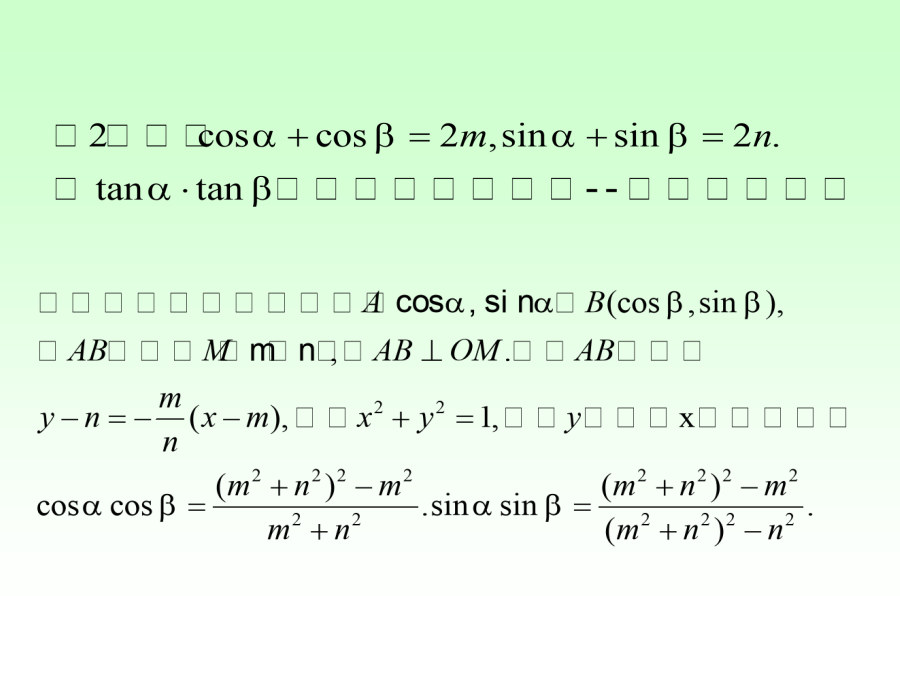

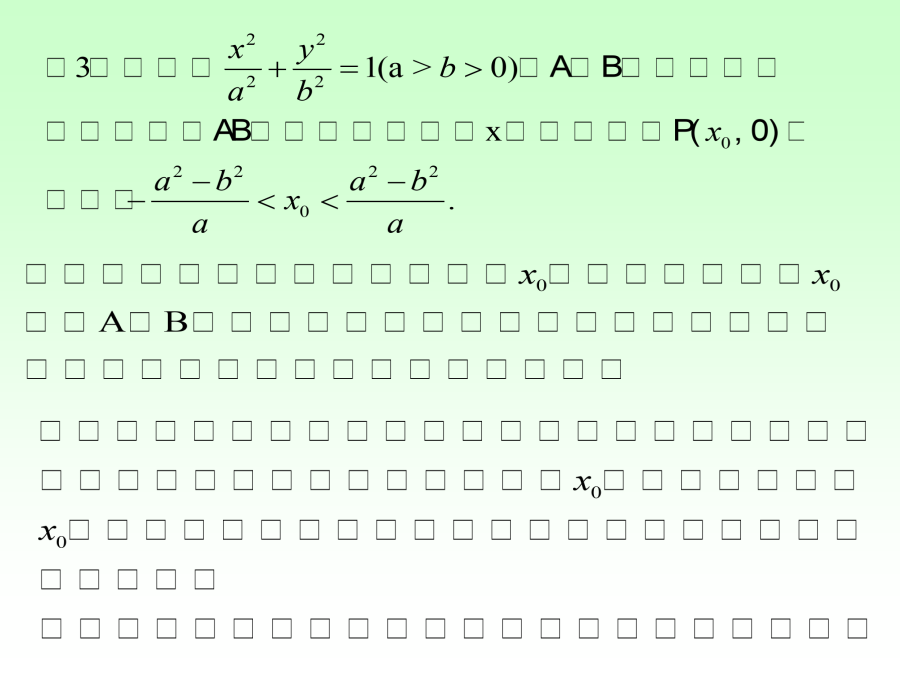
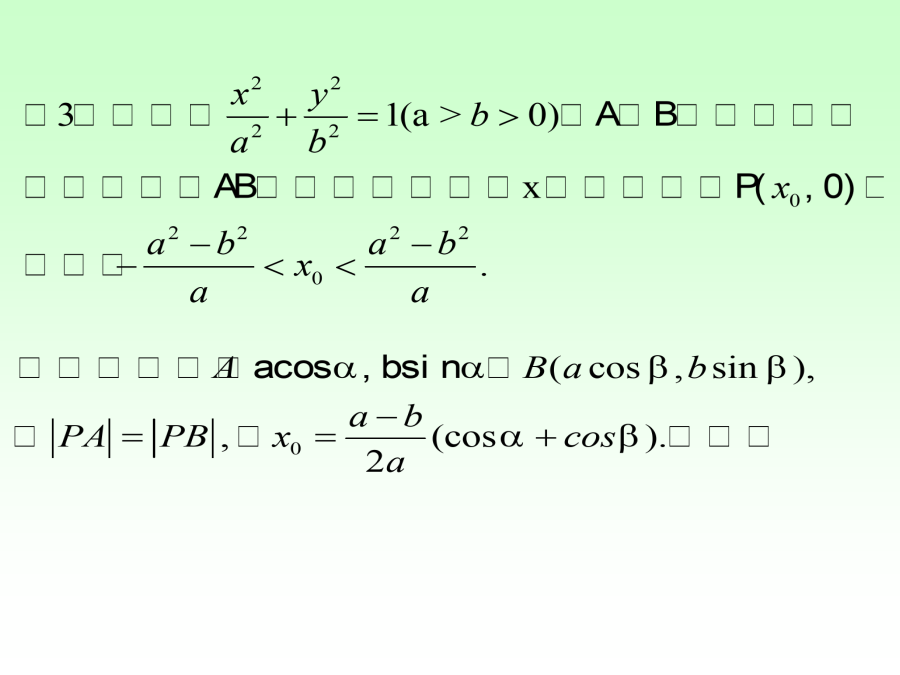
亲,该文档总共43页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第七章数学解题的思维过程.ppt
第七章数学解题的思维过程第一节解题过程的思维分析解题的过程是思维的过程,其中既有逻辑思维,又有直觉思维;有分析与综合、抽象与概括、比较与类比,也有归纳与猜想、观察与尝试、想象与顿悟,是一个极其复杂的心理过程。一、“观察----联想----转化”解题“三部曲”1、观察是联想的基础,在观察中认识特征观察是人们认识事物、增长知识的最基本的途径,是发现和解决问题的前提。观察是积极的,有意识的,而不应是消极的、被动的。通过由整体到部分,再由部分到整体的观察,有意识地去寻找各种特征、联系,从比较中发现问题,从变化中寻

数学解题的思维过程.doc
数学解题的思维过程数学解题的思维过程是指从理解问题开始经过探索思路转换问题直至解决问题进行回顾的全过程的思维活动。对于数学解题思维过程可简要总结为弄清问题、拟定计划、实现计划和回顾。这四个阶段思维过程的实质可以用下列八个字加以概括:理解、转换、实施、反思。第一阶段:理解问题是解题思维活动的开始。第二阶段:转换问题是解题思维活动的核心是探索解题方向和途径的积极的尝试发现过程是思维策略的选择和调整过程。第三阶段:计划实施是解决问题过程的实现它包含着一系列基础知识和基本技能的灵活运用和思维过程的具

高三数学六数学解题思维过程素材.doc
2六、数学解题思维过程数学解题的思维过程是指从理解问题开始,从经过探索思路,转换问题直至解决问题,进行回顾的全过程的思维活动。在数学中,通常可将解题过程分为四个阶段:第一阶段是审题。包括认清习题的条件和要求,深入分析条件中的各个元素,在复杂的记忆系统中找出需要的知识信息,建立习题的条件、结论与知识和经验之间的联系,为解题作好知识上的准备。第二阶段是寻求解题途径。有目的地进行各种组合的试验,尽可能将习题化为已知类型,选择最优解法,选择解题方案,经检验后作修正,最后确定解题计划。第三阶段是实施计划。将计划的所

高三数学六数学解题思维过程素材.doc
2六、数学解题思维过程数学解题的思维过程是指从理解问题开始从经过探索思路转换问题直至解决问题进行回顾的全过程的思维活动。在数学中通常可将解题过程分为四个阶段:第一阶段是审题。包括认清习题的条件和要求深入分析条件中的各个元素在复杂的记忆系统中找出需要的知识信息建立习题的条件、结论与知识和经验之间的联系为解题作好知识上的准备。第二阶段是寻求解题途径。有目的地进行各种组合的试验尽可能将习题化为已知类型选择最优解法选择解题方案经检验后作修正最后确定解题计划。第三阶段是实施计划。将计划的所有细节实际

高三数学六数学解题思维过程素材.doc
2六、数学解题思维过程数学解题的思维过程是指从理解问题开始从经过探索思路转换问题直至解决问题进行回顾的全过程的思维活动。在数学中通常可将解题过程分为四个阶段:第一阶段是审题。包括认清习题的条件和要求深入分析条件中的各个元素在复杂的记忆系统中找出需要的知识信息建立习题的条件、结论与知识和经验之间的联系为解题作好知识上的准备。第二阶段是寻求解题途径。有目的地进行各种组合的试验尽可能将习题化为已知类型选择最优解法选择解题方案经检验后作修正最后确定解题计划。第三阶段是实施计划。将计划的所有细节实际
