
第四章_杆件横截面上的剪应力(材料力学课件).ppt

kp****93


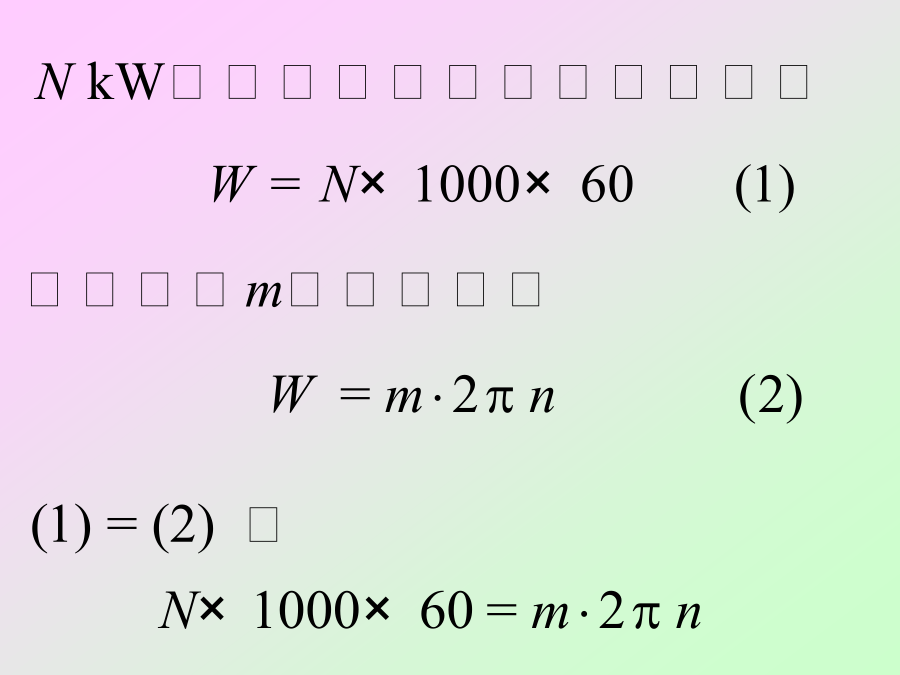
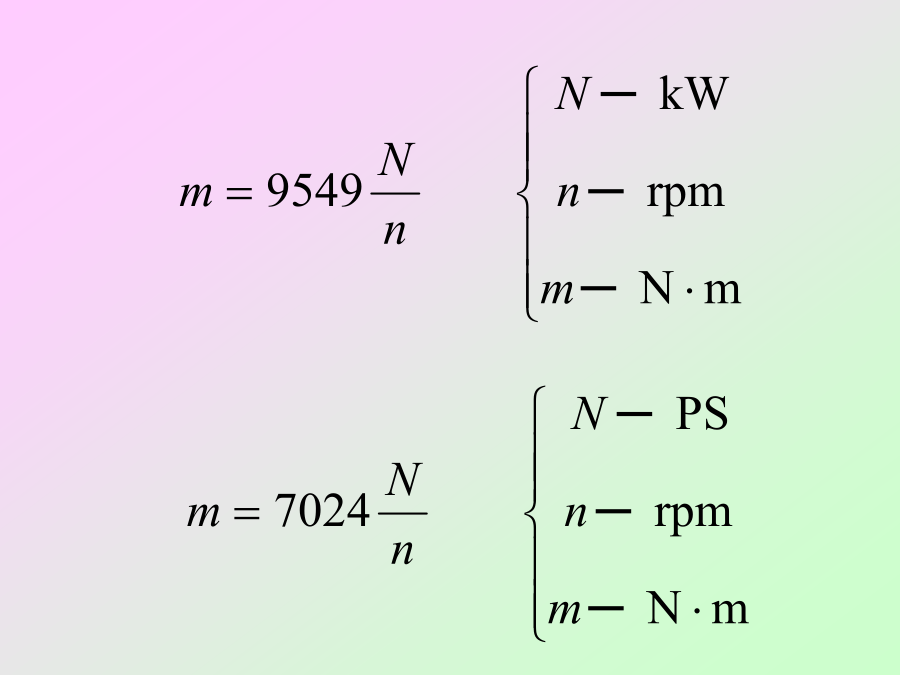


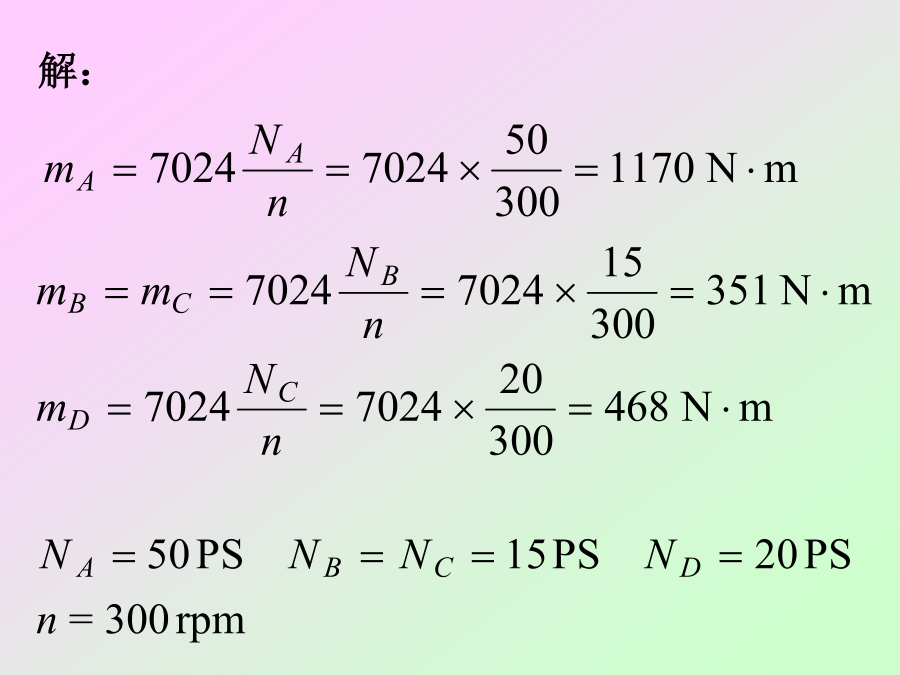
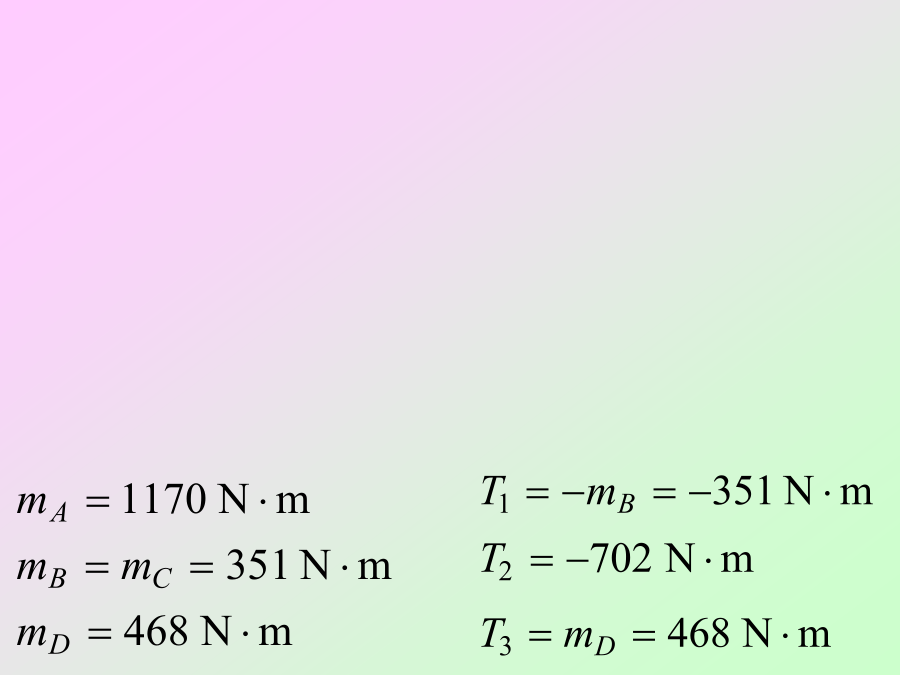
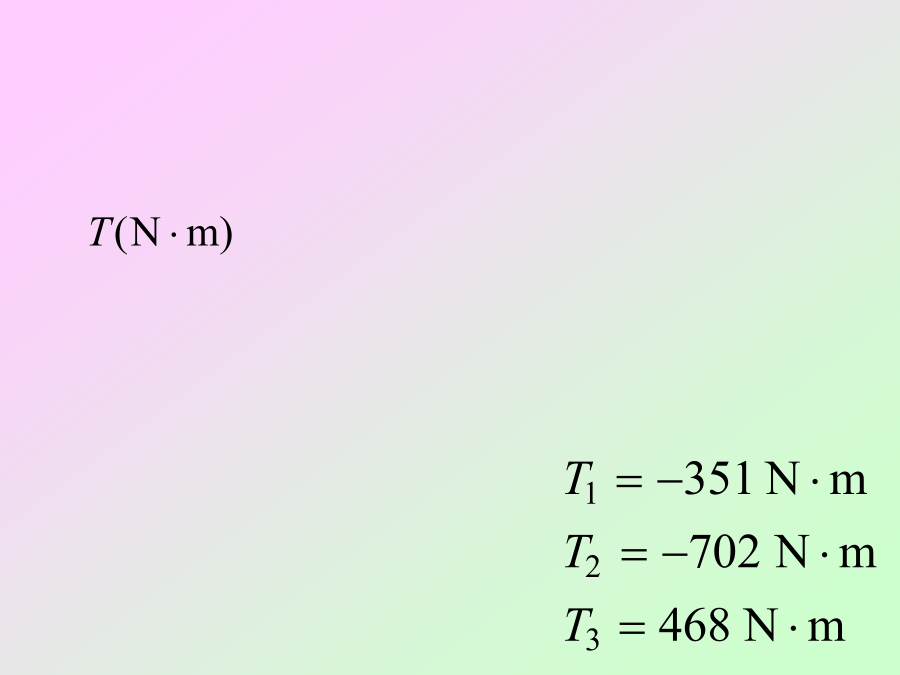

亲,该文档总共56页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第四章_杆件横截面上的剪应力(材料力学课件).ppt
第四章杆件横截面上的剪应力外力偶矩的计算:GB3101-93中规定的数值方程式表示方法例:图示传动轴,主动轮A输入功率NA=50马力,从动轮B、C、D输出功率分别为NB=NC=15马力,ND=20马力,轴的转速为n=300转/分。作轴的扭矩图。解:薄壁圆筒的扭转实验:剪应力在截面上均匀分布,方向垂直于半径根据精确的理论分析,当t≤r/10时,上式的误差不超过4.52%,是足够精确的。剪应力互等定理:在相互垂直的两个平面上,剪应力一定成对出现,其数值相等,方向同时指向或背离两平面的交线。剪切胡克定律:薄壁圆

右面杆的横截面上只有剪应力.ppt
第三章扭转§3–1概述§3–2传动轴的外力偶矩·扭矩及扭矩图§3–3薄壁圆筒的扭转§3–4等直圆杆在扭转时的应力·强度分析§3–5等直圆杆在扭转时的变形·刚度条件§3–6等直圆杆的扭转超静定问题内容提要一、工程实例3、机器中的传动轴工作时受扭。二、扭转的概念扭转角():任意两截面绕轴线转动而发生的角位移。剪应变():直角的改变量。§3–2传动轴的外力偶矩·扭矩及扭矩图从动轮n——轴的转速(r/min)nnm用平行于杆轴线的坐标表示横截面的位置,用垂直于杆轴线的坐标表示横截面上的扭矩,从而绘制出表示扭矩

河海大学-材料力学----杆件横截面上的应力应变分析.pptx
§3-2直杆轴向拉压时横截面上的正应力1、几何(变形)关系3、静力学关系圣维南原理(Saint—Venantprinciple)将原力系用静力等效的新力系来替代,除了对原力系作用附近的应力分布有明显影响外,在离力系作用区域略远处(距离约等于截面尺寸),该影响就非常微小。根据这一原理,杆件上复杂的外力系就可以用简单的力系取代。在离外力作用截面略远处,仍然可用正应力的计算公式计算应力。意义:弹性体某一局部区域的复杂外力系,可用静力等效的简单力系来代替。三、应力集中(stressconcentration)用塑

杆件横截面上的应力.ppt
杆件横截面上的应力第一节基本概念应力:杆件截面上的分布内力集度杆原长为l,直径为d。受一对轴向拉力F的作用,发生变形。变形后杆长为l1,直径为d1。胡克定律实验表明,在比例极限内,杆的轴向变形Δl与外力F及杆长l成正比,与横截面积A成反比。即:F横截面----是指垂直杆轴线方向的截面;斜截面----是指任意方位的截面。试计算图示杆件1-1、2-2、和3-3截面上正应力.已知横截面面积A=2×103mm2试求图示结构AB杆横截面上的正应力。已知F=30KN,A=400mm2图示直杆,其抗拉刚度为EA,试求杆

弹性杆件横截面上的内力计算.doc
弹性杆件横截面上的内力计算概念题1.判断题:(以下结论对者画√,错者画×)(1)轴力的大小等于外力的大小。()(2)杆件拉压或扭转变形时,截面上的内力只与其所受的外力有关。与其他因素无关。()(3)当轴的两端受到一对大小相等、转向相反的力偶作用时,轴将产生扭转变形。()(4)在纯扭转变形时,在有外力偶作用的截面处,扭矩图在该处发生突变,且突变值等于外力偶矩的大小。()(5)梁弯曲变形时,截面上的内力只与其所受的外力有关。与其他因素无关。()(6)梁弯曲变形,在计算截面的弯矩时,无论用截面哪一侧的外力计算,
