运筹学课件 第十一章 存 贮 论.ppt

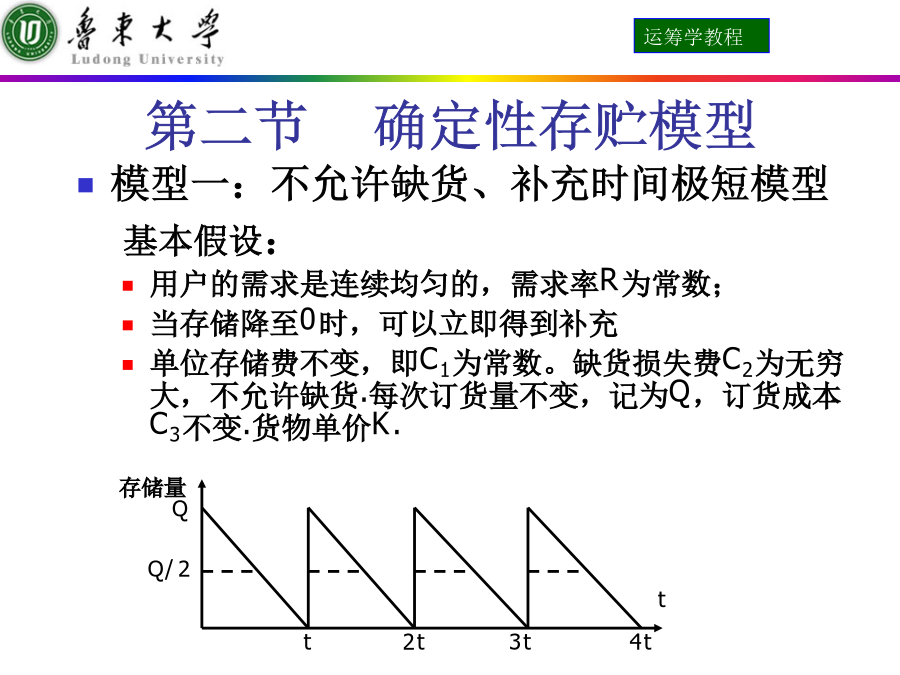
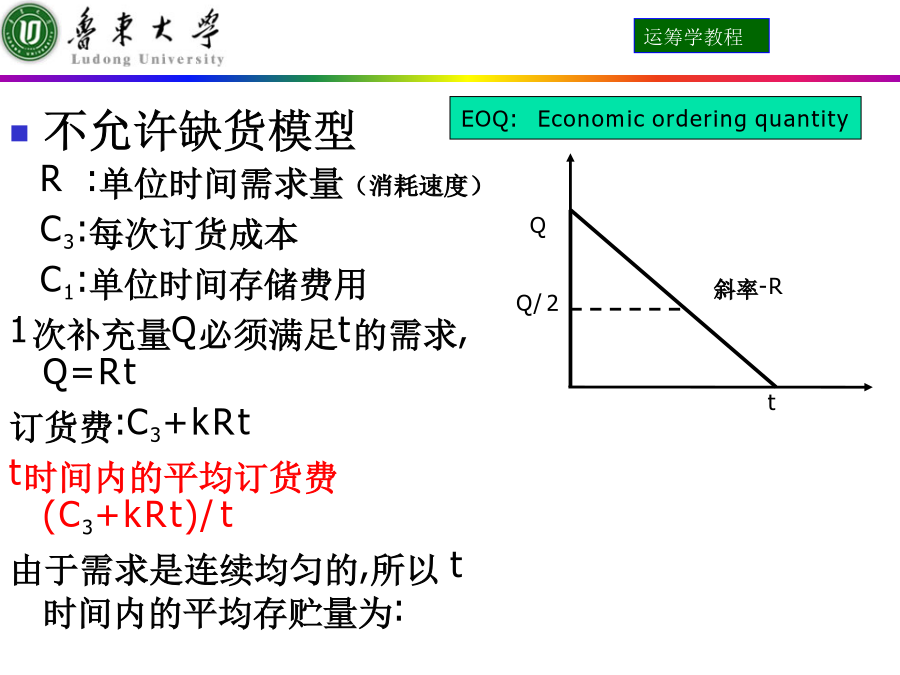
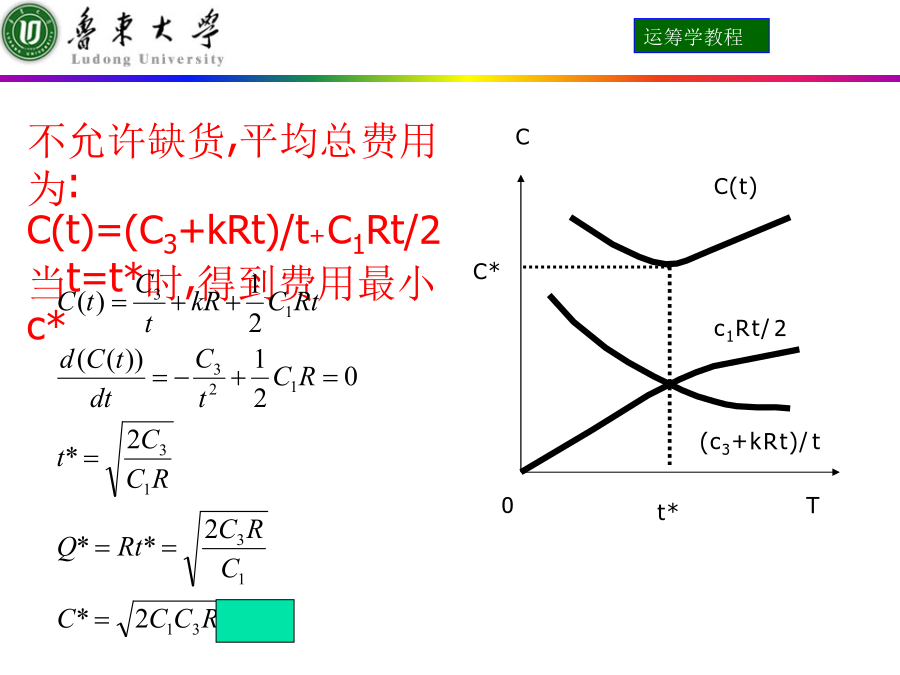
第十一章存贮论第一节存贮问题及其基本概念库存模型：

库存模型的基本问题：
如何使库存相关的总成本最小？
应该库存什么商品？
补充库存时，每次的补充量是多少？
应该间隔多长时间来补充库存？二、库存问题基本概念
需求：生产消费需求，从存储系统中减少
需求量:单位时间的需求（需求率）
连续输出与间断输出
均匀输出与非均匀输出
确定输出与随机输出

补充Q：从供应商或生产中补充到存储系统
提前时间：提前备货（订货）的时间
拖后时间：订货推迟时间
经济批量：成本最低时每次订货量Q*费用C：
存贮费：每存储单位物质单位时间存储费用
订货费：采购的费用；
1、每订一次货的订货费用，与量无关，
2、购买商品的进货成本。
生产费：自行生产所需要的费用。
缺货费:不允许缺货时，缺货损失费无限大
目标函数：单位时间平均成本或费用总和最小
变量是单位时间内订货次数和每一次的订货量
各类成本和需求的单位时间必须保持一致
价格不变时购置成本对最优解没有影响
不允许缺货时，缺货损失费也可不考虑存贮策略
指决定什么什么情况下对存贮进行补充，以及补充的数量的多少。
（1）t-循环策略：不论实际的存贮状态如何，总是每隔一个固定的时间t，补充一个固定的存贮量。
（2）（t,S）策略：每隔一个固定的时间t，补充一次，补充的数量以补足一个固定的最大存贮量S为准。每次补充的数量是不固定的，根据实际存贮量而定，当存贮（余额）为I，补充的数量Q=S-I.
（3）（s,S）策略：当存贮（余额）为I，,如果I>s，则不对存贮进行补充；如果I≤s，则对存贮进行补充，补充的数量Q=S-I.补充后达到最大存贮量S.s为订货点。
（t,s,S）策略:每隔一个固定的时间t盘点一次，得知当时的存贮I,根据存贮I是否超过订货点s，决定是否定货、数量。第二节确定性存贮模型不允许缺货模型
R:单位时间需求量（消耗速度）
C3:每次订货成本
C1:单位时间存储费用
1次补充量Q必须满足t的需求,Q=Rt
订货费:C3+kRt
t时间内的平均订货费(C3+kRt)/t
由于需求是连续均匀的,所以t时间内的平均存贮量为:

平均存货费用为:C1Rt/2不允许缺货,平均总费用为:
C(t)=(C3+kRt)/t+C1Rt/2
当t=t*时,得到费用最小c*
不允许缺货模型
R:单位时间需求量（消耗速度）
C3:每次订货成本
C1:单位时间存储费用
平均存货水平＝Q/2
使总平均费用最小的

单位时间内次数N0=R/Q*
订货周期t*=Q*/R
例:某商店经售商品，成本单价5元，每天存储费用为成本的0.1％，需求量为100件/天，需求为均匀，该商品的一次定购费用为10元，假设该商品可以随时到货，求经济批量(EOQ)和最低成本。
解：K=5元/件，C1=5X0.1％元/件.天,C3=10元,R=100件/天模型二：允许缺货，生产需一定时间
（生产系统；经济生产批量）
基本假设：
生产需要一定时间，设生产批量为Q，所需时间为t，速度P=Q/t
需求速度为R(R<P),生产的产品一部分满足需求，剩余部分才作为存储。
模型二：允许缺货，补充时间较长
模型假设条件：
允许缺货（需要补足），生产需要周期，生产速度p>R,
企业可以在存储降至0后，还可以再等一段时间然后订货，订货后立刻可以得到补充。前提是顾客遇到缺货时损失很小,并且会耐心等待直到新的补充到来。允许缺货从经济的观点来看对企业是有利的。tt在模型二中，取消允许缺货和补充需要一定的时间，C2=∞,P=∞,模型二为模型一。
注意：t1*=t2*=t3*=0;
A*=Q*;B*=0模型三：不允许缺货，补充时间较长
基本假设：
在模型二的假设条件中，不允许缺货，C2=∞,t2=0
某企业月需求为30件,需求速度为常数.该商品每件进价300元,月存贮费为进价的2%,向工厂订购该商品每次的订货费每次20元,订购后需5天才开始到货,到货速度为2件/天,求最优存贮策略.模型四：允许缺货（需要补足），补充时间很短（立刻可以补充p=∞）
其余同模型二.模型四：允许缺货（需要补足），补充时间很短（立刻可以补充P=∞）模型五:价格与订货批量有关的存储模型当订购量为Q时，一个周期内所需费用为：

模型五最小平均费用订购批量Q*计算步骤：工厂每周需要零部件32箱,c1=1元/周.箱,每次订购费用25元,不允许缺货.零件进货时如果(1)定货1-9箱,每箱12元;(2)定货10-49箱,每箱10元;(3)定货50-99箱,每箱9.5元;(4)定货大于99箱,每箱9元,求最优存贮策略.第三节单周期随机性存储模型模型六：需求为随机的单一周期存储模型
模型假设：
需求服从一定的分布；
单一周期存储只考虑一个周期，到周期结束时存储应为0，通常采用降价处理方式。
报童问题：
报