
简单复合函数的导数.doc

dc****76




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

简单复合函数的导数.doc
选修2-2导数及其应用§1.2.3简单复合函数的导数(总第52课时)一、【目的要求】(1)掌握求复合函数的导数的法则;(2)熟练求简单复合函数的导数。二、【重点难点】复合函数的求导法则是本节课的重点与难点。三、【知识回顾】1、常见函数的导数公式:;;(C为常数);(为常数);;;;;。2、导数的四则运算法则:=________四、引入:1、试求:的导数。解法1:展开后求导知;解法2:,两者得到的结论不一致,显然解法2是存在问题的。那究竟存在什么问题呢?我们先从今天学的复合函数说起。2、什么是复合函数?由几

简单复合函数的导数.doc
选修2-2导数及其应用§1.2.3简单复合函数的导数(总第52课时)一、【目的要求】(1)掌握求复合函数的导数的法则;(2)熟练求简单复合函数的导数。二、【重点难点】复合函数的求导法则是本节课的重点与难点。三、【知识回顾】1、常见函数的导数公式:;;(C为常数);(为常数);;;;;。2、导数的四则运算法则:=________四、引入:1、试求:的导数。解法1:展开后求导知;解法2:,两者得到的结论不一致,显然解法2是存在问题的。那究竟存在什么问题呢?我们先从今天学的复合函数说起。2、什么是复合函数?由几

简单复合函数的导数.doc
§1.2.3简单复合函数的导数(总第52课时)一、【目的要求】(1)掌握求复合函数的导数的法则;(2)熟练求简单复合函数的导数。二、【重点难点】复合函数的求导法则是本节课的重点与难点。三、【知识回顾】1、常见函数的导数公式:;;(C为常数);(为常数);;;;;。2、导数的四则运算法则:=________四、引入:1、试求:的导数。解法1:展开后求导知;解法2:,两者得到的结论不一致,显然解法2是存在问题的。那究竟存在什么问题呢?我们先从今天学的复合函数说起。2、什么是复合函数?由几个基本初等函数复合而成
简单复合函数的导数.pdf
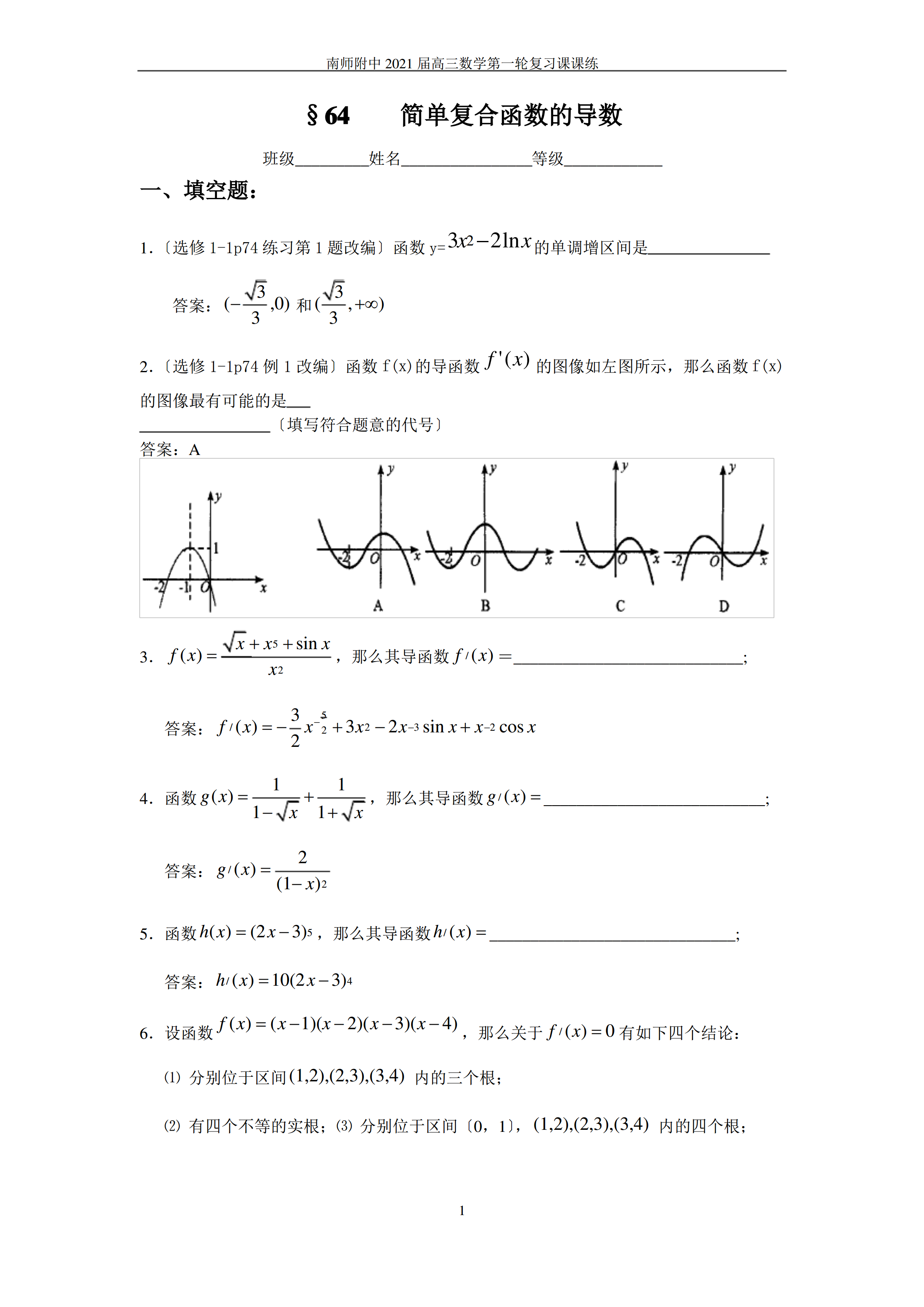
南师附中2021届高三数学第一轮复习课课练§64简单复合函数的导数班级_________姓名________________等级____________一、填空题:1.〔选修1-1p74练习第1题改编〕函数y=3x22lnx的单调增区间是33答案:(,0)和(,)332.〔选修1-1p74例1改编〕函数f(x)的导函数f'(x)的图像如左图所示,那么函数f(x)的图像最有可能的是〔填写符合题意的代号〕答案:Axx5sinx3.f(x),那么其导函数f/(x)=________________

简单复合函数的导数.doc
选修2-2导数及其应用§1.2.3简单复合函数的导数(总第52课时)一、【目的要求】(1)掌握求复合函数的导数的法则;(2)熟练求简单复合函数的导数。二、【重点难点】复合函数的求导法则是本节课的重点与难点。三、【知识回顾】1、常见函数的导数公式:;;(C为常数);(为常数);;;;;。2、导数的四则运算法则:=________四、引入:1、试求:的导数。解法1:展开后求导知;解法2:,两者得到的结论不一致,显然解法2是存在问题的。那究竟存在什么问题呢?我们先从今天学的复合函数说起。2、什么是复合函数?由几
