预览加载中，请您耐心等待几秒...

221、222直线与平面平行、平面与平面平行的判定.pptx

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共52页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

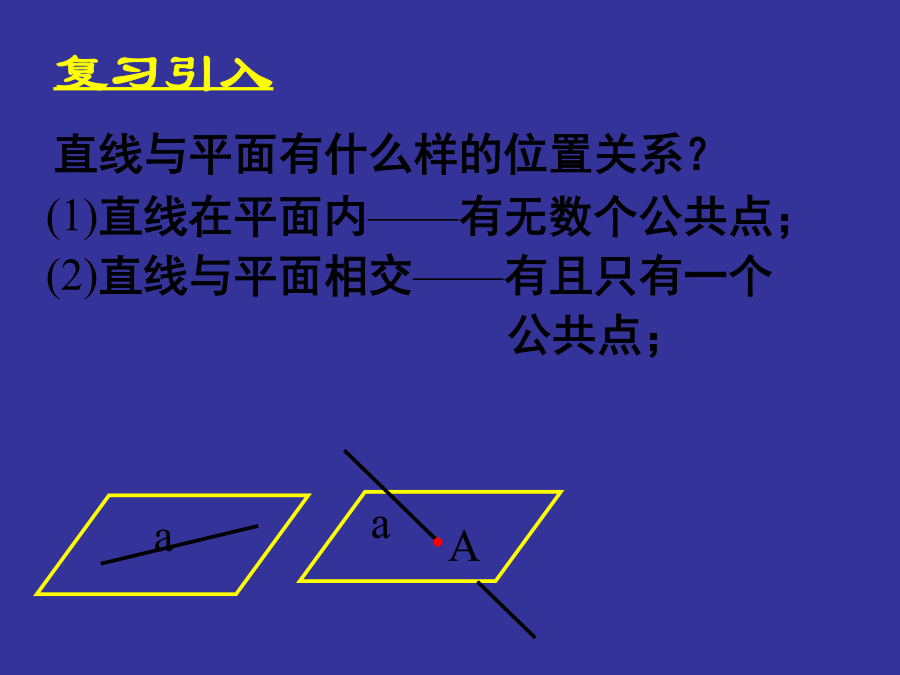
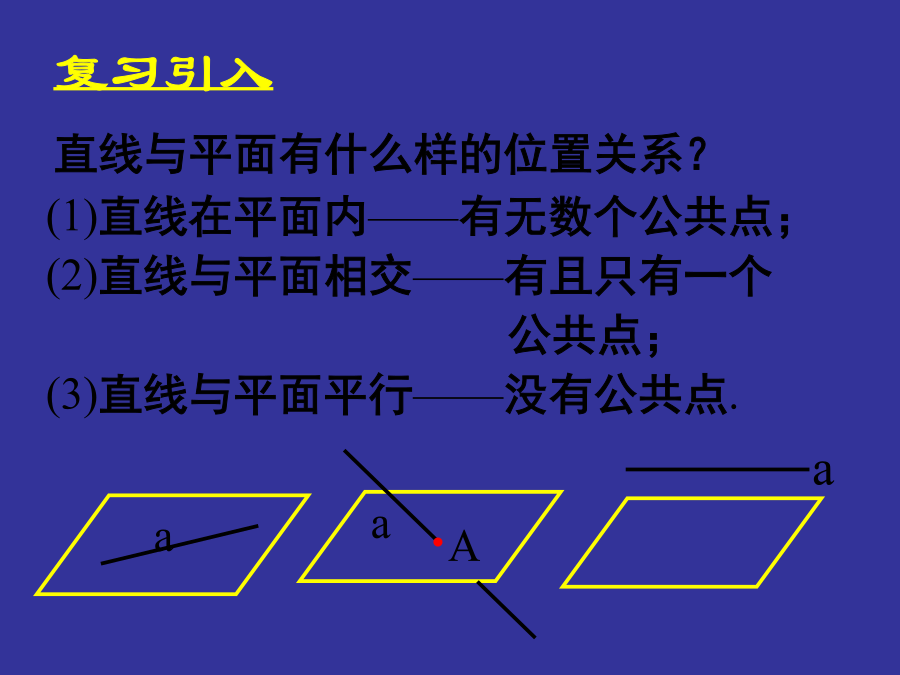
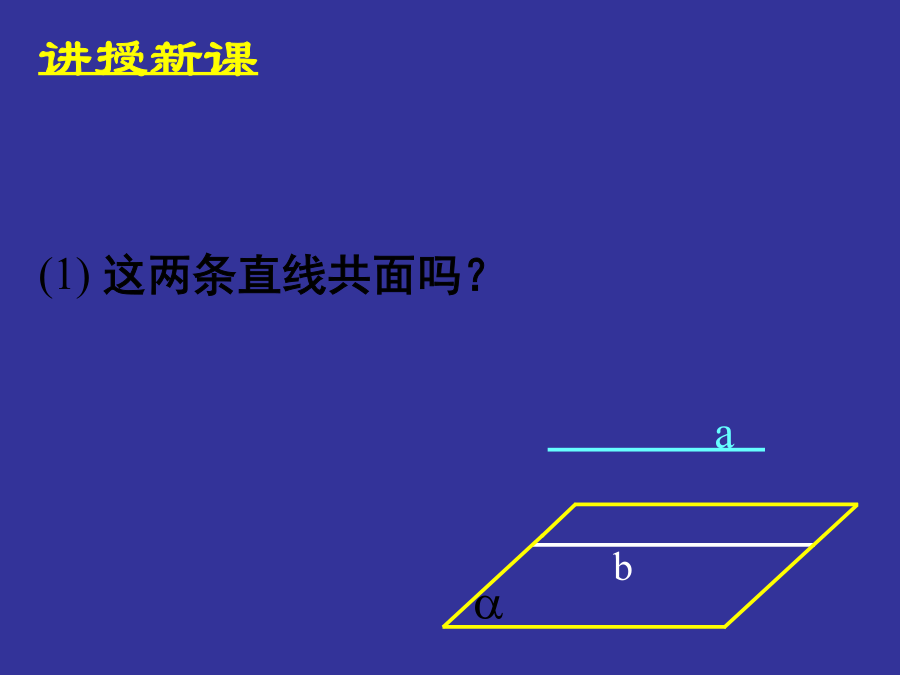
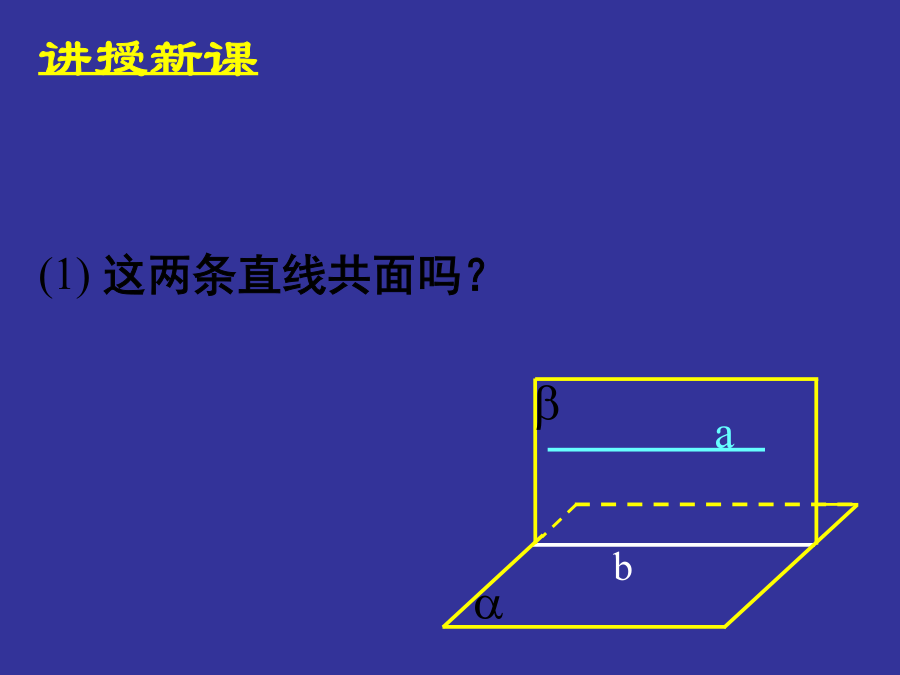
复习引入复习引入复习引入复习引入讲授新课讲授新课平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行.平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行.平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行.符号表示：符号表示：感受校园生活中线面平行的例子:感受校园生活中线面平行的例子:感受校园生活中线面平行的例子:练习练习练习练习定理的应用定理的应用定理的应用________________.________________.变式2变式2变式2巩固练习定义：如果两个平面没有公共点，那么这两个平面互相平行，也叫做平行平面.定义：如果两个平面没有公共点，那么这两个平面互相平行，也叫做平行平面.若平面内有一条直线与平面平行，那么，平行吗？若平面内有一条直线与平面平行，那么，平行吗？若平面内有一条直线与平面平行，那么，平行吗？若平面内有一条直线与平面平行，那么，平行吗？若平面内有一条直线与平面平行，那么，平行吗？一个平面内的两条相交直线与另一个平面平行，则这两个平面平行.一个平面内的两条相交直线与另一个平面平行，则这两个平面平行.平面与平面平行的判定定理3.棱长为a的正方体AC1中，设M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行.课堂小结1.复习本节课内容，理清脉络；2.《习案》第十一课时.