
狄拉克方程省名师优质课赛课获奖课件市赛课一等奖课件.ppt

你相****光吗








亲,该文档总共43页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

狄拉克方程省名师优质课赛课获奖课件市赛课一等奖课件.ppt
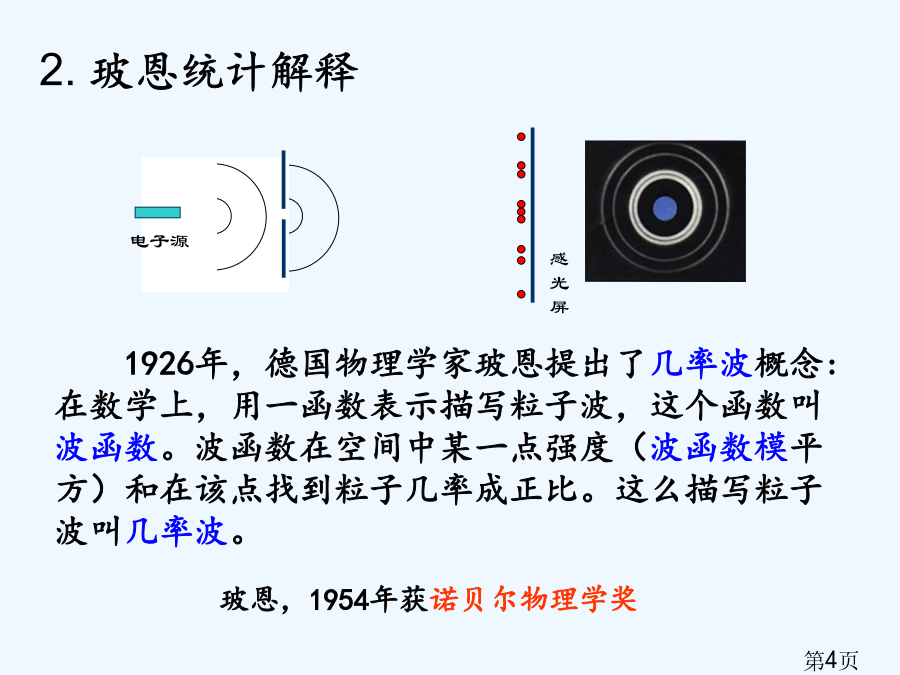
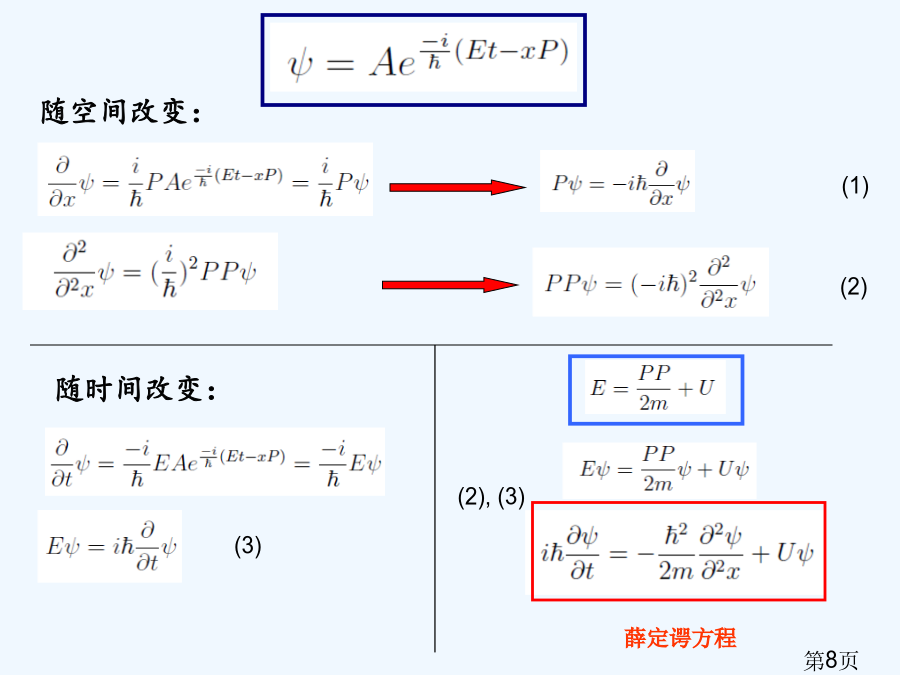
《高等量子力学》狄拉克方程内容提要一、波函数和薛定谔方程粒子在t时刻r点出现几率薛定谔方程薛定谔方程引入3.薛定谔方程(三维)二、克莱因-戈尔登方程3.自由粒子解德布罗意波保罗·狄拉克:英国理论物理学家,量子力学奠基者之一。薛定谔方程因为不是相对论性,它必定要向相对论扩展。克莱因-戈登方程就是第一个相对论性波动方程,然而却不能计算氢原子,且一直为负能态和负概率所困扰,所以长久不被物理学家所接收。狄拉克方程正是在这种困境中应运而生。它融合了狭义相对论、海森伯矩阵力学、薛定谔波动力学三方理论,能够计算氢原子光

狄拉克方程1省名师优质课赛课获奖课件市赛课一等奖课件.ppt
《高等量子力学》狄拉克方程内容提要一、波函数和薛定谔方程粒子在t时刻r点出现几率薛定谔方程薛定谔方程引入3.薛定谔方程(三维)二、克莱因-戈尔登方程3.自由粒子解德布罗意波保罗·狄拉克:英国理论物理学家,量子力学奠基者之一。薛定谔方程因为不是相对论性,它必定要向相对论扩展。克莱因-戈登方程就是第一个相对论性波动方程,然而却不能计算氢原子,且一直为负能态和负概率所困扰,所以长久不被物理学家所接收。狄拉克方程正是在这种困境中应运而生。它融合了狭义相对论、海森伯矩阵力学、薛定谔波动力学三方理论,能够计算氢原子光

《蒹葭》获奖省名师优质课赛课获奖课件市赛课一等奖课件.ppt
蒹葭学习目标解题在水一方一、听读:感受诗音乐美蒹葭苍苍,白露为霜。所谓伊人,在水一方。溯洄从之,道阻且长;溯游从之,宛在水中央。蒹葭萋萋,白露未晞。所谓伊人,在水之湄。溯洄从之,道阻且跻;溯游从之,宛在水中坻。蒹葭采采,白露未已,所谓伊人,在水之涘。溯洄从之,道阻且右;溯游从之,宛在水中沚。检验字词掌握情况。朗诵课文,疏通文意。蒹葭/苍苍,白露/为霜。所谓/伊人,在水/一方。溯洄/从之,道阻/且长。溯游/从之,宛在/水中央。蒹葭/萋萋,白露/未晞。所谓/伊人,在水/之湄。溯洄/从之,道阻/且跻。溯游/从之

《蒹葭》获奖省名师优质课赛课获奖课件市赛课一等奖课件.ppt
蒹葭学习目标解题在水一方一、听读:感受诗音乐美蒹葭苍苍,白露为霜。所谓伊人,在水一方。溯洄从之,道阻且长;溯游从之,宛在水中央。蒹葭萋萋,白露未晞。所谓伊人,在水之湄。溯洄从之,道阻且跻;溯游从之,宛在水中坻。蒹葭采采,白露未已,所谓伊人,在水之涘。溯洄从之,道阻且右;溯游从之,宛在水中沚。检验字词掌握情况。朗诵课文,疏通文意。蒹葭/苍苍,白露/为霜。所谓/伊人,在水/一方。溯洄/从之,道阻/且长。溯游/从之,宛在/水中央。蒹葭/萋萋,白露/未晞。所谓/伊人,在水/之湄。溯洄/从之,道阻/且跻。溯游/从之

《祝福》省名师优质课赛课获奖课件市赛课一等奖课件.ppt
祝福鲁迅(1881~1936),原名周樟寿,后更名周树人。中国当代伟大文学家、思想家和革命家,新文学奠基人。小说集:《呐喊》《彷徨》历史小说集:《故事新编》散文集:《朝花夕拾》又名《旧事重提》散文诗集:《野草》杂文集:《南腔北调集》《坟》《热风》等《祝福》是鲁迅小说代表作之一,也是鲁迅第二个小说集《彷徨》中第一篇。鲁迅小说含有最清醒现实主义精神,为中国当代文学艺术殿堂塑造了第一批不朽经典形象,如阿Q、闰土、祥林嫂、孔乙己等。《祝福》写于1924年2月7日,是鲁迅短篇小说集《彷徨》第一篇。最初发表于1924
