菱形的性质与判定综合应用.ppt

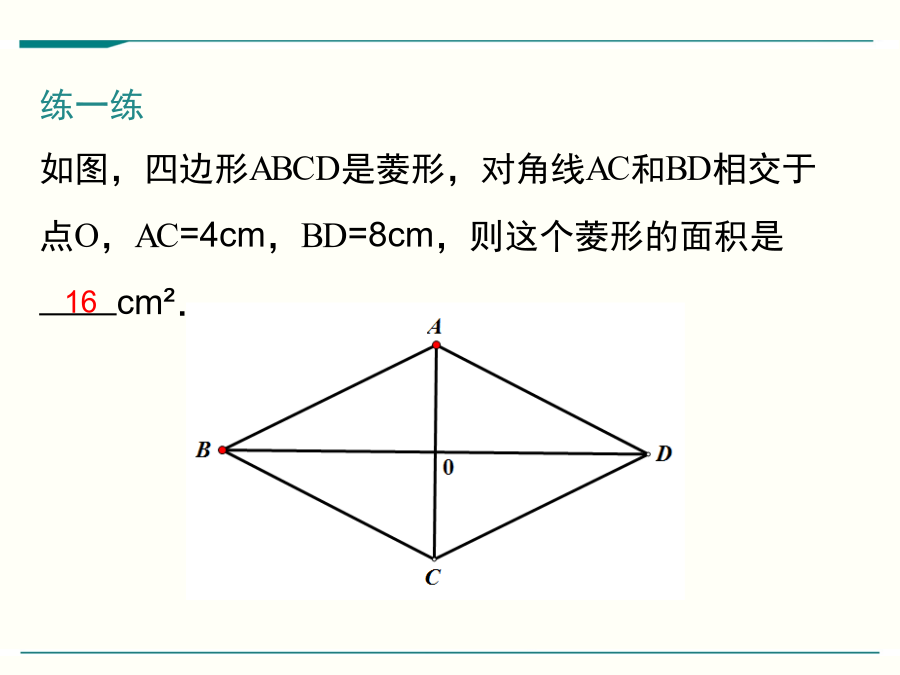
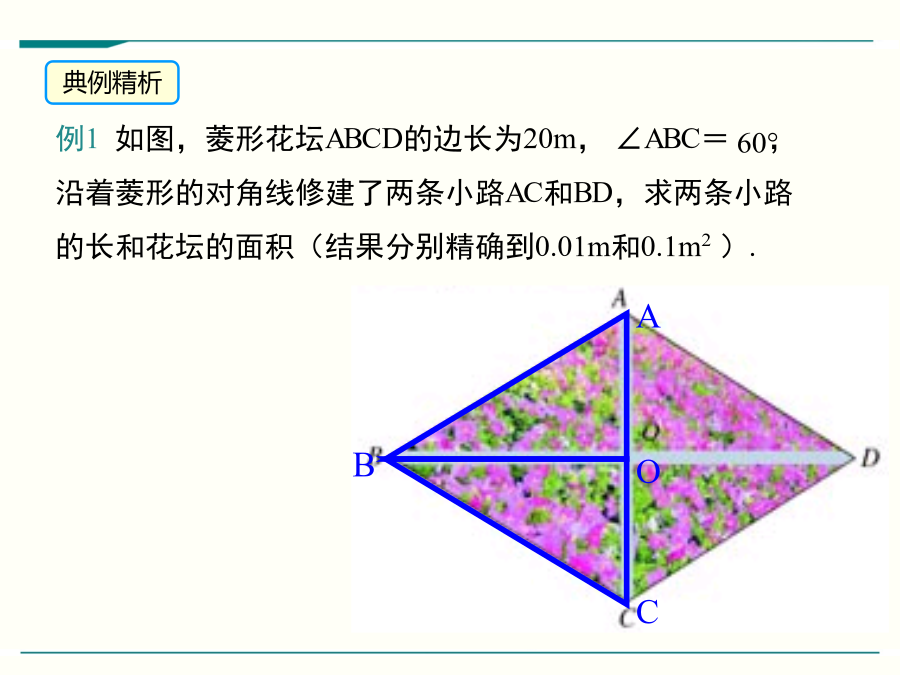
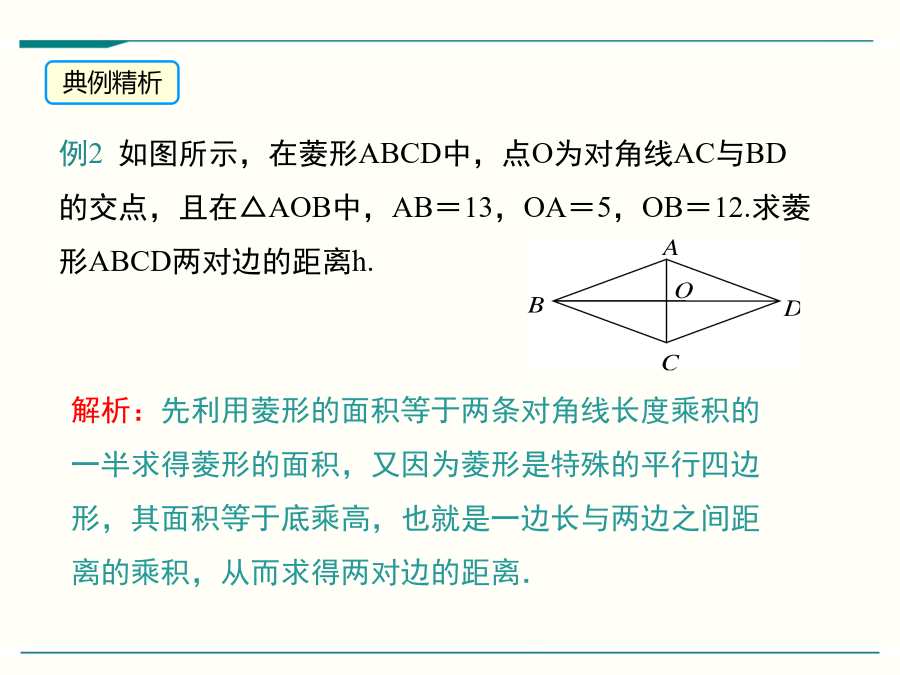
1.能灵活运用菱形的性质定理及判定定理解决一
些相关问题,并掌握菱形面积的求法。(重点、难点)
2.经历菱形性质定理及判定定理的应用过程,体会
数形结合、转化等思想方法。1．平行四边形的对边，对角，对角线 ．
2．菱形具有 的一切性质．
3．菱形是 图形也是 图形．
4．菱形的四条边都 ．
5．菱形的两条对角线互相．6.平行四边形的面积=_________.练一练
如图，四边形ABCD是菱形，对角线AC和BD相交于
点O，AC=4cm，BD=8cm，则这个菱形的面积是
cm²．

例1如图，菱形花坛ABCD的边长为20m，∠ABC＝，沿着菱形的对角线修建了两条小路AC和BD，求两条小路的长和花坛的面积（结果分别精确到0.01m和0.1m2）.例2如图所示，在菱形ABCD中，点O为对角线AC与BD的交点，且在△AOB中，AB＝13，OA＝5，OB＝12.求菱形ABCD两对边的距离h.
方法总结：菱形的面积计算有如下方法：
(1)一边长与两对边的距离(即菱形的高)的积；
(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍)；
(3)两条对角线长度乘积的一半．如图两张等宽的纸条交叉重叠在一起，重叠的部分ABCD是什么图形？为什么？典例精析(2)解：∵∠BCF＝120°，
∴∠EBC＝60°，
∴△EBC是等边三角形，
∴菱形的边长为4，高为，
∴菱形的面积为.1.已知菱形的周长是24cm，那么它的边长是______.4.如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.求：
（1）对角线AC的长度；
（2）菱形ABCD的面积.5.如图，在菱形ABCD中，对角线AC与BD相交于点O，∠BAD=60°，BD=6，求菱形的边长AB和对角线AC的长.
解：∵四边形ABCD是菱形，
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD=BD=×6=3(菱形的对角线互相平分)
在等腰三角形ABC中，
∵∠BAD=60°，
∴△ABD是等边三角形.
∴AB=BD=6.在RtΔAOB中，由勾股定理，得
OA2+OB2=AB2，
∴OA===
∴AC=2OA=（菱形的对角线相互平分）.课堂小结本课时书后习题