条件概率与乘法公式省名师优质课赛课获奖课件市赛课一等奖课件.ppt

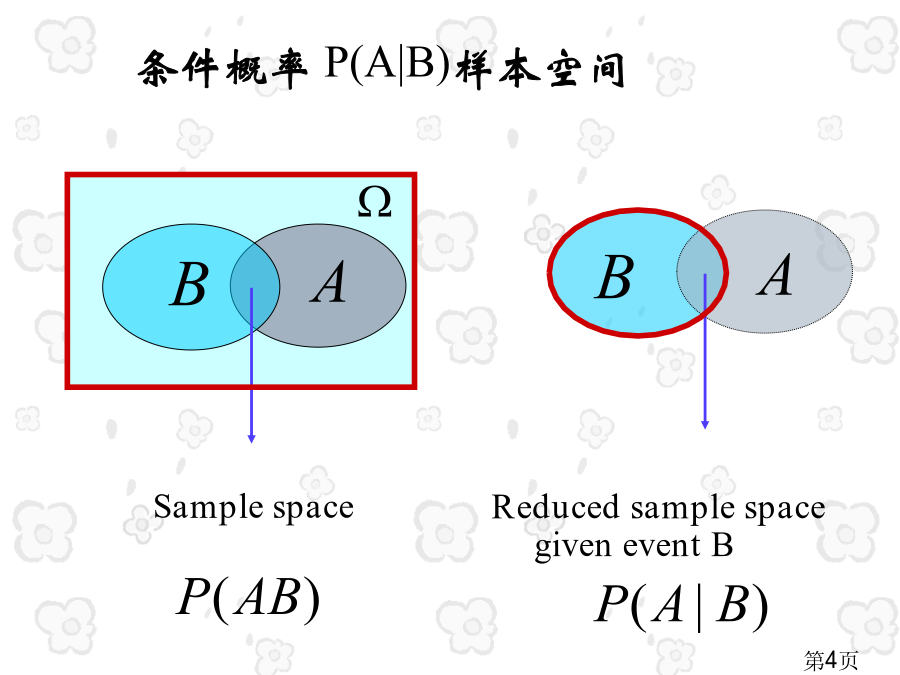
条件概率与乘法公式条件概率ConditionalProbability设Ａ，Ｂ为同一个随机试验中两个随机事件,且Ｐ（Ｂ）＞０，则称概率P(A|B)与P(AB)区分与联络例设100件产品中有70件一等品，25件二等品，要求一、二等品为合格品．从中任取1件，求(1)取得一等品概率；(2)已知取得是合格品，求它是一等品概率．例考虑恰有两个小孩家庭.若已知某一家有男孩，求这家有两个男孩概率；若已知某家第一个是男孩，求这家有两个男孩（相当于第二个也是男孩）概率.（假定生男生女为等可能）乘法法则一批产品中有4%次品，而合格品中一等品占45%.从这批产品中任取一件，求该产品是一等品概率．解练一练练一练练一练全概率公式与解设Ａ1，Ａ2，...，Ａn组成一个完备事件组，且Ｐ(Ａi)＞0，i＝1，2，...，n，则对任一随机事件Ｂ，有例设播种用麦种中混有一等，二等，三等，四等四个等级种子，分别各占95.5％，2％，1.5％，1％，用一等，二等，三等，四等种子长出穗含50颗以上麦粒概率分别为0.5，0.15，0.1，0.05，求这批种子所结穗含有50颗以上麦粒概率．贝叶斯公式Bayes’Theorem设A1，A2，…,An组成完备事件组，且诸P（Ai）>0)B为样本空间任意事件，P（B）>0,则有例设某工厂有甲、乙、丙三个车间生产同一个产品，已知各车间产量分别占全厂产量25%，35%，40%，而且各车间次品率依次为5%，4%，2%．现从待出厂产品中检验出一个次品，试判断它是由甲车间生产概率．甲箱中有3个白球，2个黑球，乙箱中有1个白球，3个黑球。现从甲箱中任取一球放入乙箱中，再从乙箱任意取出一球。问从乙箱中取出白球概率是多少？已知在全部男子中有5%，在全部女子中有0.25%患有色盲症。随机抽一人发觉患色盲症，问其为男子概率是多少？（设男子和女子人数相等）。