
用样本的频率分布估计总体分布课堂教学素材示范课市名师优质课比赛一等奖市公开课获奖课件.pptx

和蔼****娘子







亲,该文档总共26页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

用样本的频率分布估计总体分布课堂教学素材示范课市名师优质课比赛一等奖市公开课获奖课件.pptx
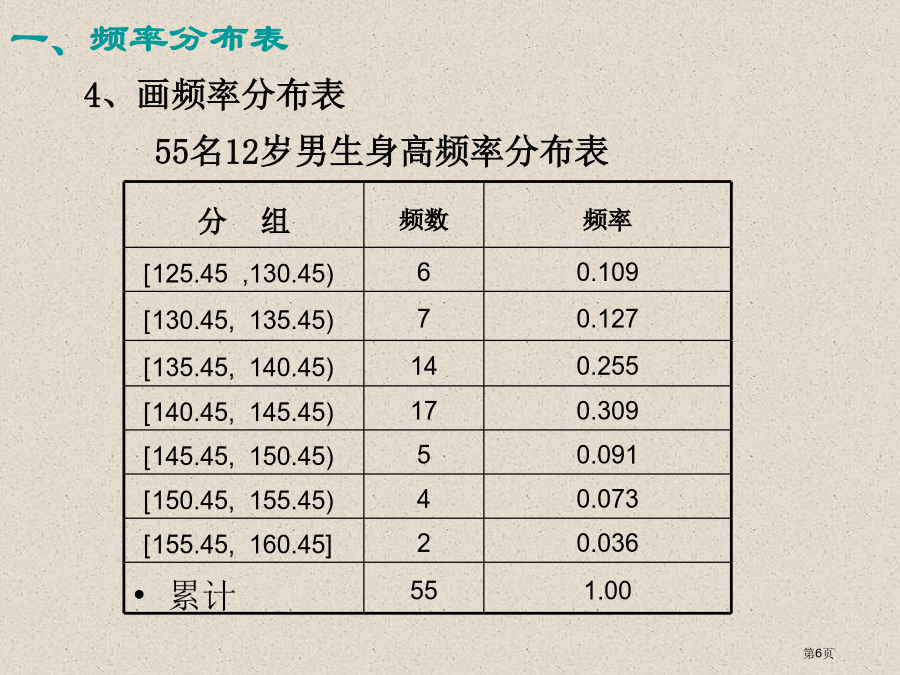
第二章统计2.2.1用样本频率分布预计总体分布用样本预计总体抽查某地域55名12岁男生身高(单位:cm)测量值以下:128.1144.4150.3146.2140.6126.0125.6127.7154.4142.7141.2142.7137.6136.9132.3131.8147.7138.4136.6136.2141.6141.1133.1142.8136.8133.1144.5142.4140.8127.7150.7160.3138.8154.3147.9141.3143.8138.1139.714

用样本频率分布估计总体频率分布.ppt
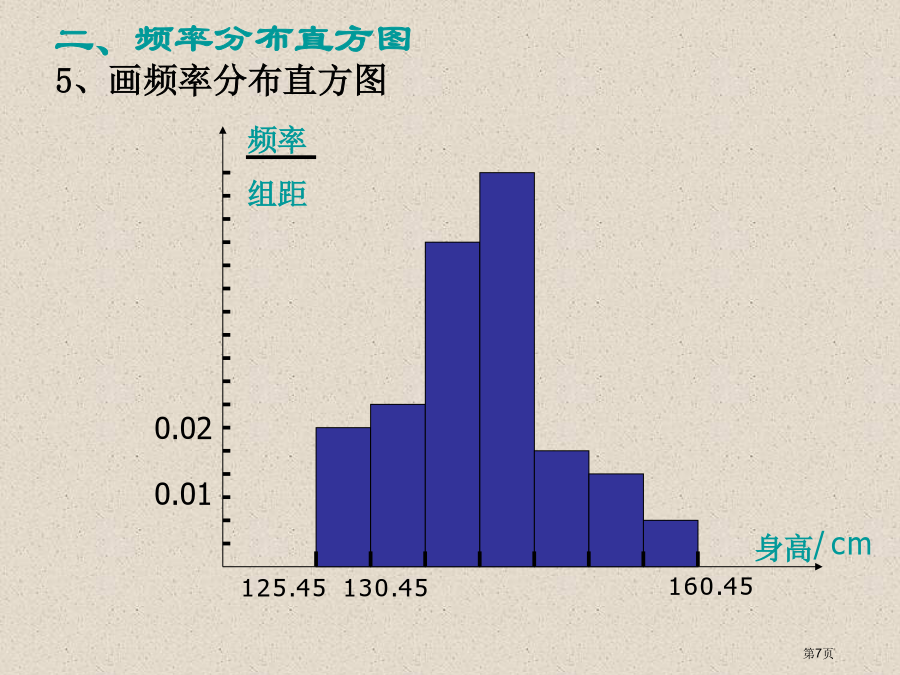
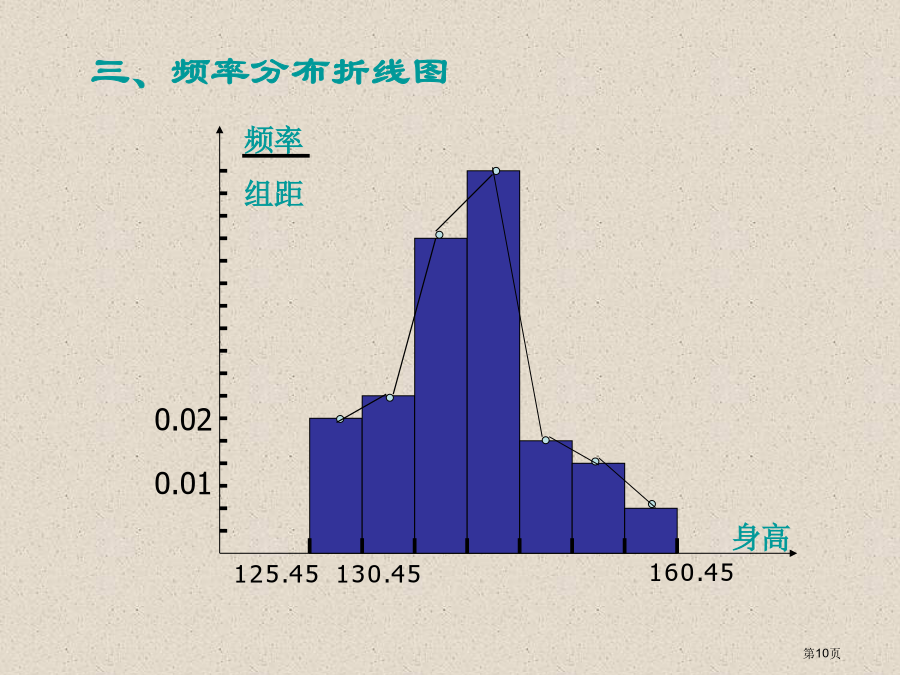
(1)某校有1000名学生,其中O型血的有400人,A型血的人有250人,B型血的有250人,AB型血的有100人,为了研究血型与色弱的关系,要从中抽取一个40人的样本,按分层抽样,O型血应抽取的人数为___人,A型血应抽取的人数为___人,B型血应抽取的人数为___人,AB型血应抽取的人数为___人。频率分布表和频率分布直方图1、求极差(即一组数据中最大值与最小值的差)知道这组数据的变动范围4.3-0.2=4.1频率分布直方图如下:频率分布直方图如下:频率分布直方图如下:频率分布直方图如下:练习解:组距

用样本的频率分布估计总体的频率分布.ppt
探索知识2.2.1用样本的频率分布估计总体分布用样本的频率分布估计总体分布我国是世界上严重缺水的国家之一,城市缺水问题较为突出。某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超过a的部分按议价收费。通过抽样,我们获得了100位居民某年的月平均用水量(单位:t),如下表:分析数据的一种基本方法是用图将它们画出来,或者用紧凑的表格改变数据的排列方式。频数分布直方图1.求极差(即一组数据中最大值与最小值的差):4.列频率分布表频率分布
用样本的频率分布估计总体的频率分布.ppt
用样本的频率分布估计总体分布一、日清检测:二、学习目标:三、自主学习四、合作探究列频率分布表画频率分布直方图五、教师小结探究2教师小结:六、当堂检测:

用样本的频率分布估计总体分布公开课.pptx
数据我国是世界上严重缺水的国家之一,城市缺水问题较为突出.2010年全国主要城市中缺水情况排在前10位的城市邯郸市市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超过a的部分按议价收费.3.1很容易发现的是一个居民月平均用水量的最小值时0.2t,最大值是4.3t,其他在0.2t~4.3t之间.除此之外,很难从随意记录下来的数据中直接看出规律。频率分布相关概念1、求极差(即一组数据中最大值与最小值的差)知道这组数据的变动范围4.3-0
