不等式和它的基本性质-副本.ppt

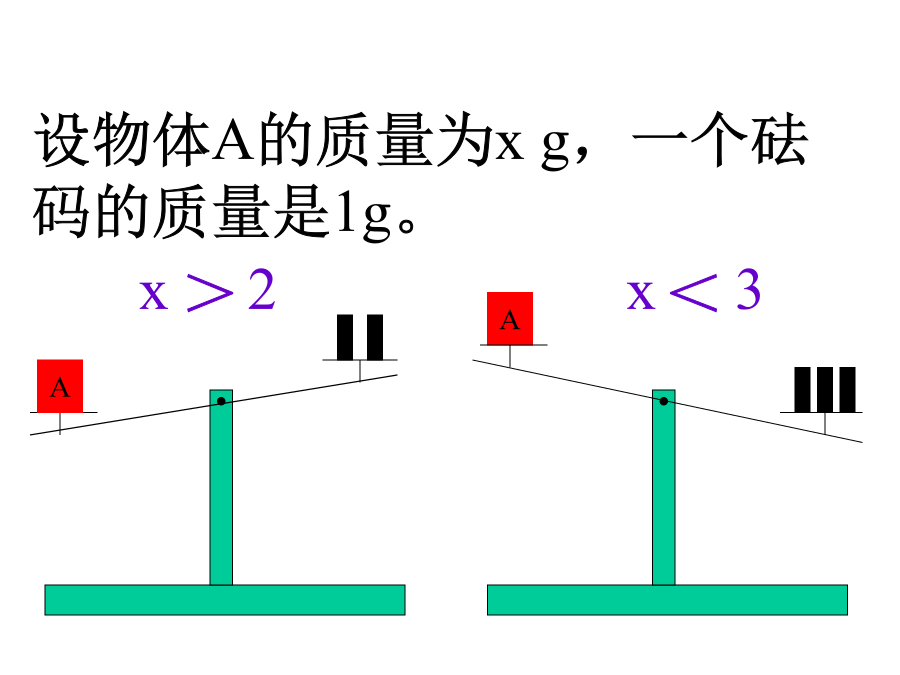
不等式和它的基本性质(1)1、气象预报，最高气温是10°C，最低气温为-5°C，可说这一天气温不低于°C，并不高于°C。-7＜-5，3+4＞1+4，x+3＜6，5+3≠12-5，a+2＞a+1，a≠0，判断下式中哪些是不等式？哪些不是？为什么？问题1：x=2及x=3是否为方程x+3=6的解？问题2：为什么x=2不是，x=3是呢？∞问题3：对于不等式x+3＜6，当x=2时，x+3的值是多少？它与6有什么关系？问题4：对于不等式x+3＜6，当x=3时，x+3的值是多少？它与6有什么关系？情况1：对于含有未知数的不等式来说，当未知数取某些数值时，不等式的左、右两边符合不等号所表示的大小关系。当x取下列数值时，哪些是不等式x+3＜6的解，哪些不是？-4，-2.5，0，1，3.5，4，4.5，7。-4，-2.5，0，1，3.5，4，4.5，7。当x=3.5时，x+3=3.5+3=当x=4.5时，x+3=4.5+3=例1、用不等式表示：（1）a是负数；（2）x的6倍减去3大于10；（3）y的与6的差小于1。（1）a是负数；（2）x的6倍减去3大于10（3）y的与6的差小于11、用小于号“＜”或大于号“＞”填空：（1）4-6；（2）-10；（3）-8-3；（4）-4.5-42、用“＜”或“＞”号填空：（1）7+34+3（2）7+（-3）4+（-3）（3）7×34×3（4）7×（-3）4×（-3）3、用不等式表示：（1）a是正数；（2）a是非负数；（3）a与6的和小于5；（4）x与2的差大于-1；（5）x的4倍大于7；（6）y的一半小于3。4、x=2是不是不等式x+3＞4的解？当x=1.5时呢？当x=-1时呢？4、x=2是不是不等式x+3＞4的解？当x=1.5时呢？当x=-1时呢？4、x=2是不是不等式x+3＞4的解？当x=1.5时呢？当x=-1时呢？小结：1、不等式的意义2、不等式的解3、列比较简单的不等式的有关方法，解决这类问题的关键是把文字语言正确地用符号语言表示出来。1234作业：补充：有理数x，y在数轴上的对应点的位置如图所示，用“＞”或“＜”号填空：（1）x+y0；（2）xy0；（3）x-y0。-7＜-5，3+4＞1+4，x+3＜6，5+3≠12-5，a+2＞a+1，a≠0，问题1：x=2及x=3是否为方程x+3=6的解？