高考数学总复习 5.3平面向量的数量积课件 文 新人教版B版 课件.ppt

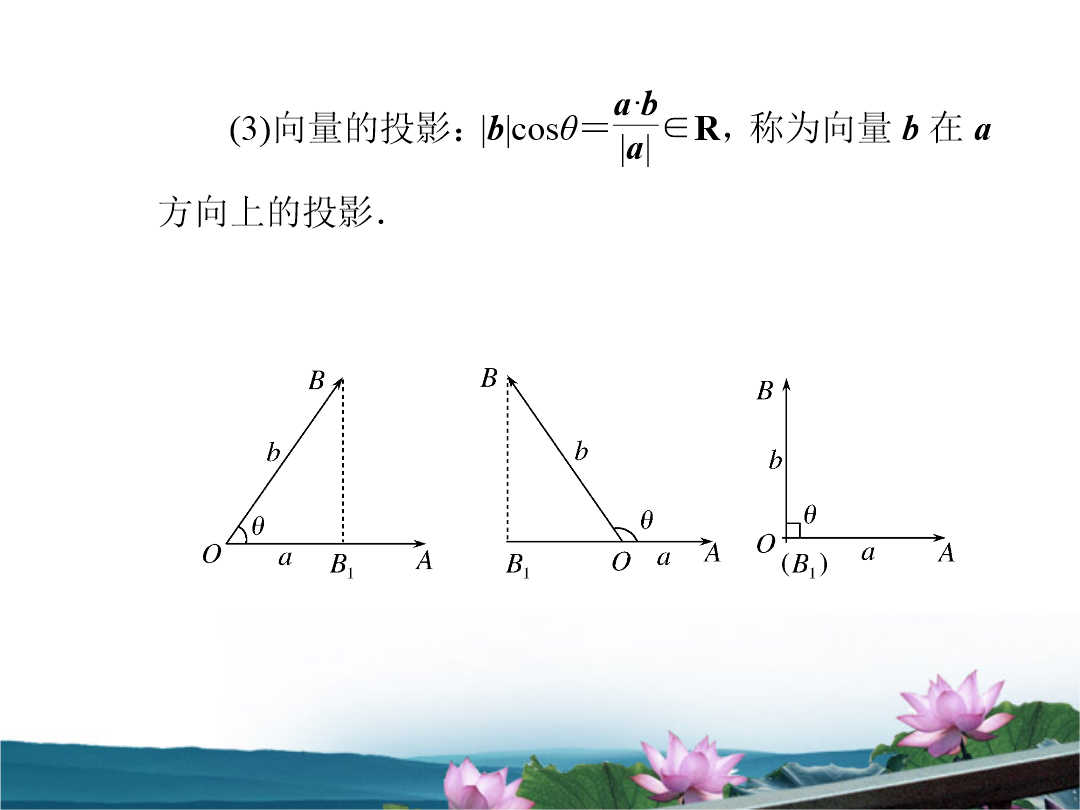
最新考纲解读1．掌握平面向量的数量积及其几何意义．2．了解用平面向量的数量积可以处理有关长度、角度和垂直的问题．3．掌握向量垂直的条件．高考考查命题趋势1．向量的数量积及运算律一直是高考数学的热点内容之一是高考命题的必选素材．考查形式多为小题考查内容主要是向量的数量积、几何意义、模以及夹角、共线和垂直问题．2．作为工具在考查三角函数、立体几何、平面解析几何等内容时经常用到．在2009年高考中有10套试卷在此知识点命题多以选择题、填空题出现如2009全国Ⅱ6；2009全国Ⅰ6；2009湖北17.3．估计在2011年高考中仍是考查热点．若单独命题则以选择题或填空题出现.注意：当且仅当两个非零向量ab同方向量时θ＝0°当且仅当ab反方向时θ＝180°当且仅当a与b垂直时θ＝90°记作a⊥b.(2)已知两个非零向量a与b它们的夹角为θ则a·b＝|a|·|b|cosθ叫做a与b的数量积(或内积)．规定：0·a＝0注意：投影的绝对值称为射影．投影是实数不是向量；而射影是非负实数．数量积的几何意义：a·b等于a的长度与b在a方向上的投影的乘积．3．平面向量数量积的运算律(1)交换律成立：a·b＝b·a(2)对实数的结合律成立：(λa)·b＝λ(a·b)＝a·(λb)(λ∈R)(3)分配律成立：(a±b)·c＝a·c±b·c＝c·(a±b)注意：(1)结合律不成立：a·(b·c)≠(a·b)·c；(2)消去律不成立a·b＝a·c不能得到b＝c.(3)a·b＝0不能得到a＝0或b＝0.4．两个非零向量垂直的充要条件a⊥b⇔a·b＝0⇔x1x2＋y1y2＝0.1.两个向量的数量积是一个实数向量加、减、数乘运算的运算结果是向量．2．数量积的记号是a·b不能写成a×b也不能写成ab.3．若a、b为实数且a·b＝0则有a＝0或b＝0但a·b＝0却不能得出a＝0或b＝0.若a、b、c∈R且a≠0则由ab＝ac可得b＝c但由a·b＝a·c及a≠0却不能推出b＝c.4．若a、b、c∈R则a(bc)＝(ab)c(结合律)成立但对于向量a、b、c(a·b)c≠a(b·c)这是因为数量a·b与c相乘是与c共线的向量而数量b·c与a相乘则是与a共线的向量所以一般二者是不等的．5．若a、b∈R则|a·b|＝|a|·|b|但对于向量a、b却有|a·b|≤|a|·|b|等号当且仅当a∥b时成立．这是因为|a·b|＝|a|·|b|·|cosθ|而|cosθ|≤1.一、选择题1．(2009年福建卷理9文12)设a、b、c为同一平面内具有相同起点的任意三个非零向量且满足a与b不共线a⊥c|a|＝|c|则|b·c|的值一定等于()A．以ab为两边的△的面积B．以bc为两边的△面积C．以ab为邻边的▱的面积D．以bc为邻边的▱的面积[答案]C[答案]C[答案]B二、填空题4．向量a、b满足(a－b)·(2a＋b)＝－4且|a|＝2|b|＝4则a、b夹角的余弦值等于________．6．已知a＝(23)b＝(－47)则a在b方向上的投影为________．7．已知|a|＝3|b|＝5如果a∥b则a·b＝________.[错误分析]忽视平行向量的概念．a、b的夹角为0°、180°.[解析]∵a∥b∴a与b夹角是0°或180°即α＝0°或180°∴a·b＝|a||b|cosα＝±15[答案]±15例1判断下列各命题正确与否：(1)0·a＝0；(2)0·a＝0；(3)若a≠0a·b＝a·c则b＝c；(4)若a·b＝a·c则b≠c当且仅当a＝0时成立；(5)对任意向量a有a2＝|a|2(6)(a·b)·c＝a·(b·c)对任意abc向量都成立；(7)a·b＝0⇒a＝0或b＝0；(8)|a·b|＝|a|·|b|(9)若a、b的夹角为θ则b在a上的投影为：b·cosθ.[解](1)错：因为实数与向量的积还是向量所以是错的．(2)对；因为向量的积是数量积所以是实数故正确．(3)错；因为a·b＝|a|·|b|cosθa·c＝|a|·|c|cosφ所以由a≠0a·b＝a·c得|b|cosθ＝|c|cosφ.因此原结论是错的．(4)错；反例：当a⊥ba⊥c时满足a·b＝a·c且b≠c但此时a不一定是零向量所以原结论是错的．(5)对；由向量的数量积定义式知是正确的．(6)错；因为(a·b)和(b·c)均是实数所以(a·b)·c与c平行而a·(b·c)与a平行a与c不一定平行所以等式不成立．(7)错；因为a·b＝|a|·|b|cosθ＝0⇒|a|＝0或|b|＝0或cosθ＝0所以原结论是错的．(8)错；因为a·b＝|a|·|b|cosθ－1≤cosθ≤1∴－|a|·|b|≤a·b≤|a|·|b|故原结论是错的．(9)错；若a、b的夹角为θ则b在a上的投影应为：|b|