
高中数学 平面向量的平行和垂直 课件苏教版必修4 课件.ppt

是你****芹呀







亲,该文档总共19页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

高中数学 平面向量的平行和垂直 课件苏教版必修4 课件.ppt
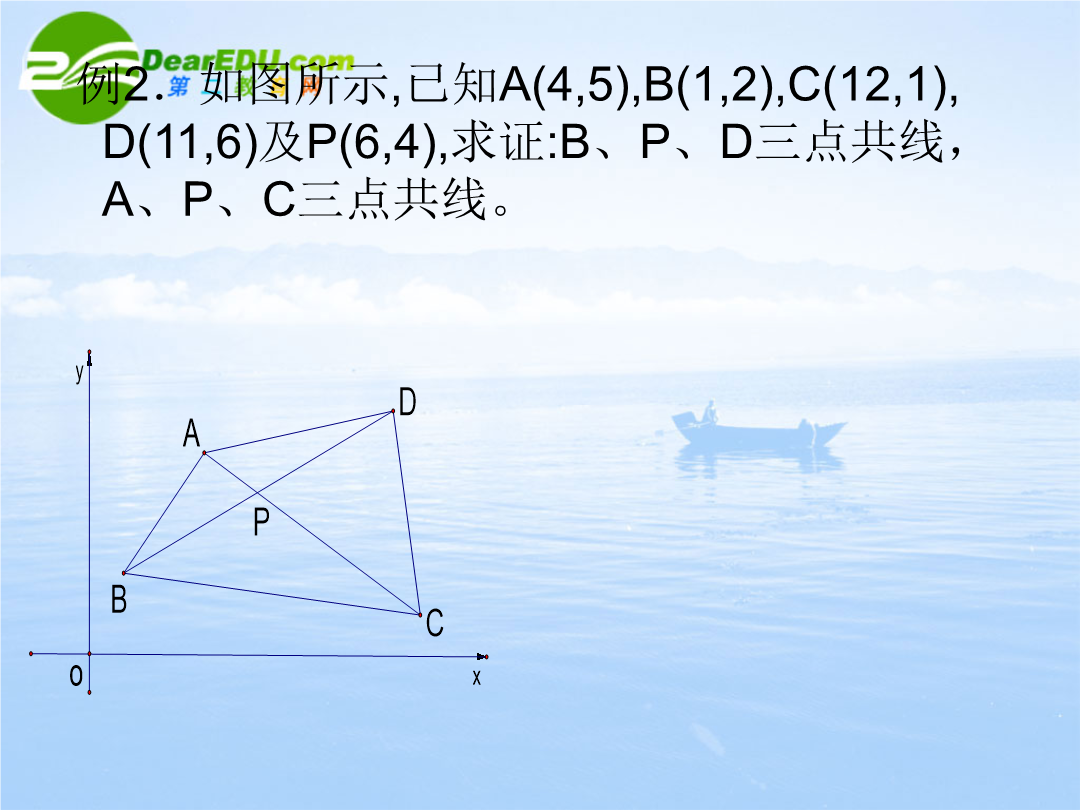
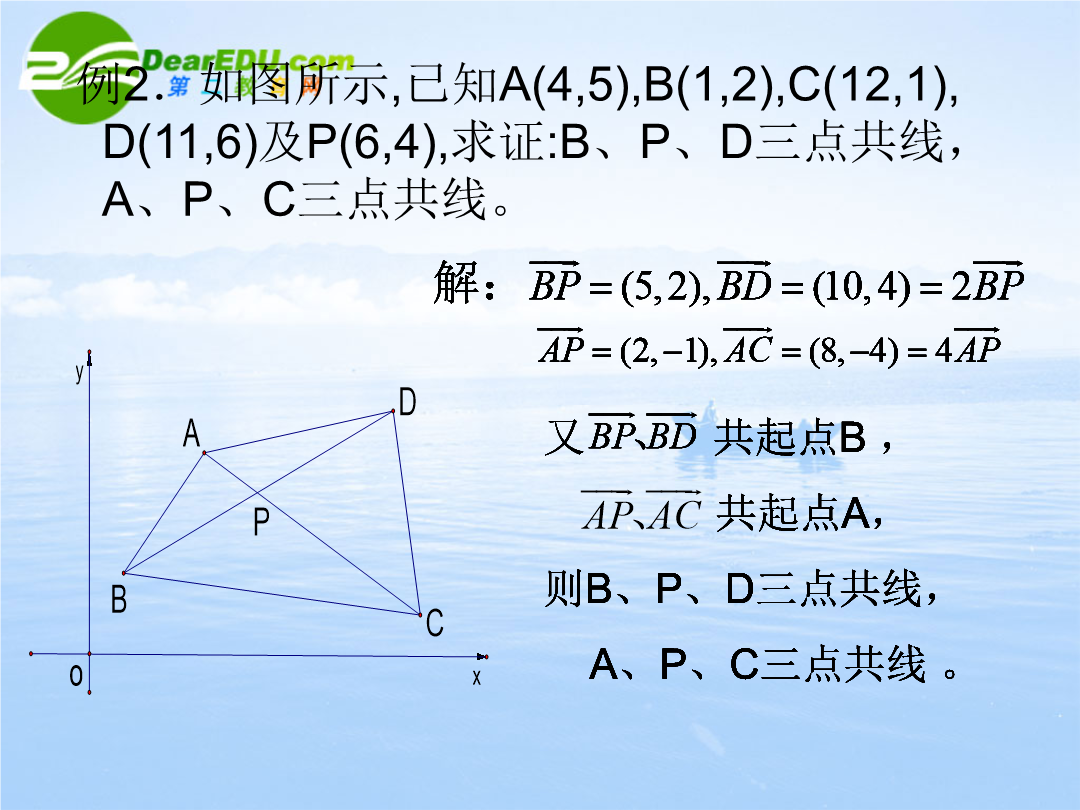
平面向量的平行与垂直基础知识回顾:1.向量共线的充要条件:符号语言:2.非零向量垂直的充要条件:符号语言:一、基础训练例1.设A(41)B(-23)C(k-6)若△ABC为直角三角形且∠B=求k的值。变式:设A(41)B(-23)C(k-6)若△ABC为直角三角形求k的值。例2.如图所示已知A(45)B(12)C(121)D(116)及P(64)求证:B、P、D三点共线A、P、C三点共线。例2.如图所示已知A(45)B(12)C(121)D(

高中数学 平面向量的平行和垂直 课件苏教必修4.ppt
平面向量的平行与垂直基础知识回顾:1.向量共线的充要条件:符号语言:2.非零向量垂直的充要条件:符号语言:一、基础训练例1.设A(41)B(-23)C(k-6)若△ABC为直角三角形且∠B=求k的值。变式:设A(41)B(-23)C(k-6)若△ABC为直角三角形求k的值。例2.如图所示已知A(45)B(12)C(121)D(116)及P(64)求证:B、P、D三点共线A、P、C三点共线。例2.如图所示已知A(45)B(12)C(121)D(

平面向量的平行与垂直ppt课件.ppt
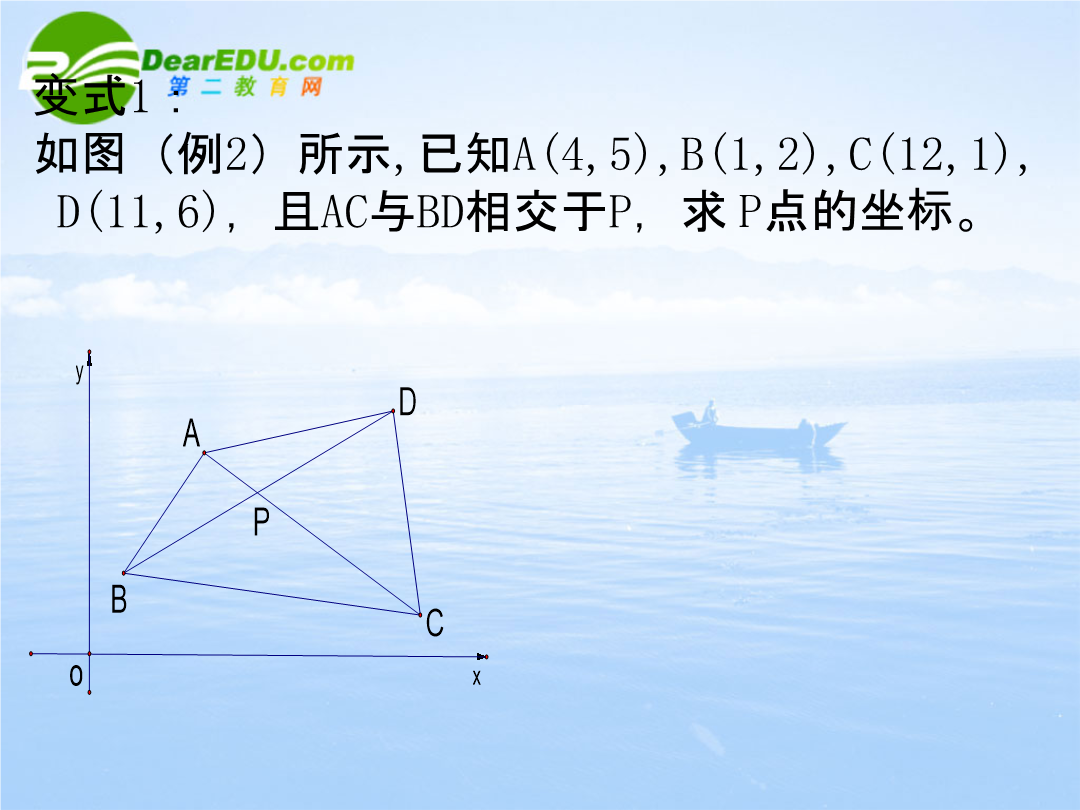
平面向量的平行与垂直基础知识回顾:一、基础训练设A(4,1),B(-2,3),C(k,-6),若△ABC为直角三角形且∠B=,求k的值。如图所示,已知A(4,5),B(1,2),C(12,1),D(11,6)及P(6,4),求证:B、P、D三点共线,A、P、C三点共线。8101112131415161718191.已知向量已知4.平面上三个向量5.已知,存在实数k和t,使得且若不等式恒成立,求a的取值范小结1.向量的平行(共线)和垂直是向量夹角的两个特殊情形:两向量平行(共线)即向量的夹角为0或,

高三数学平面向量的平行和垂直课件.ppt
平面向量的平行与垂直基础知识回顾:1.向量共线的充要条件:符号语言:2.非零向量垂直的充要条件:符号语言:一、基础训练例1.设A(41)B(-23)C(k-6)若△ABC为直角三角形且∠B=求k的值。变式:设A(41)B(-23)C(k-6)若△ABC为直角三角形求k的值。例2.如图所示已知A(45)B(12)C(121)D(116)及P(64)求证:B、P、D三点共线A、P、C三点共线。例2.如图所示已知A(45)B(12)C(121)D(

高中数学 平面向量复习与小结课件 苏教版必修4 课件.ppt
高中数学必修4实际背景二、知识梳理三、课前练习四、例题例2(1)在ΔABC中设若试以向量为基底表示向量.(2)已知O为△ABC所在平面内的一点且满足试判断△ABC的形状.例3(1)已知非零向量满足:(–
