函数的极值与导数-豆柴文库

函数的极值与导数.ppt

2024-06-16

10金币

772KB

22页

仙人****88

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共22页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

函数的极值与导数.ppt

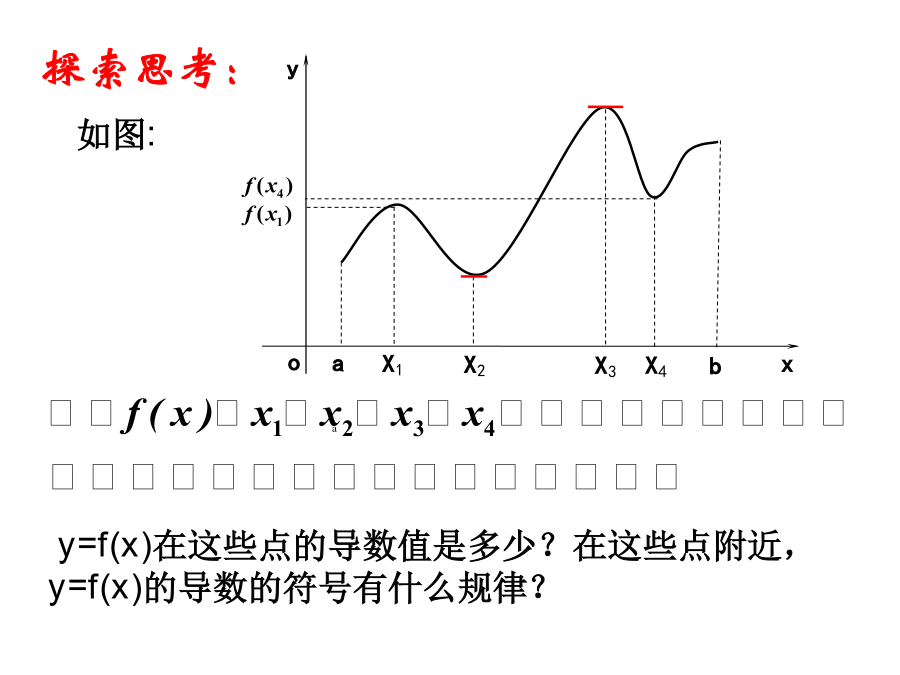
函数的极值与导数1.理解极值的有关概念．2.了解函数在某点取得极值的必要条件和充分条件．3.会用导数求函数的极大值和极小值.重点难点观察图象中，点a和点b处的函数值与它们附近点的函数值有什么的大小关系？一、极值的定义观察函数y=f(x)的图像[归纳]函数极值是在某一点附近的小区间内定义的，是局部性质。因此一个函数在其整个定义区间上可能有多个极大值或极小值，并对同一个函数来说，在某一点的极大值也可能小于另一点的极小值。结论:极值点处导数值为0探究:极值点两侧导数符号有何规律?练习：三．求函数极值的步骤(1)

2024-06-16

162KB

函数的极值与导数.ppt

1.3.2函数的极值与导数求函数单调区间的步骤关注用导数本质及其几何意义解决问题关注用导数本质及其几何意义解决问题二、新课——函数的极值:从而我们得出结论:对于可导函数,若x0满足f/(x)=0,且在x0的两侧的导数异号,则x0是f(x)的极值点,f(x0)是极值,并且:三、例题选讲:练习1练习2四.探索思考:一般地,求函数y=f(x)的极值的方法是:x补充例题2:已知函数f(x)=x3+ax2+bx+a2在x=1处有极值为10,求a、b的值.练习3:求函数的极值.练习2补充例4:已知函数f(x)=-x3

2024-06-16

772KB

函数的极值与导数.ppt

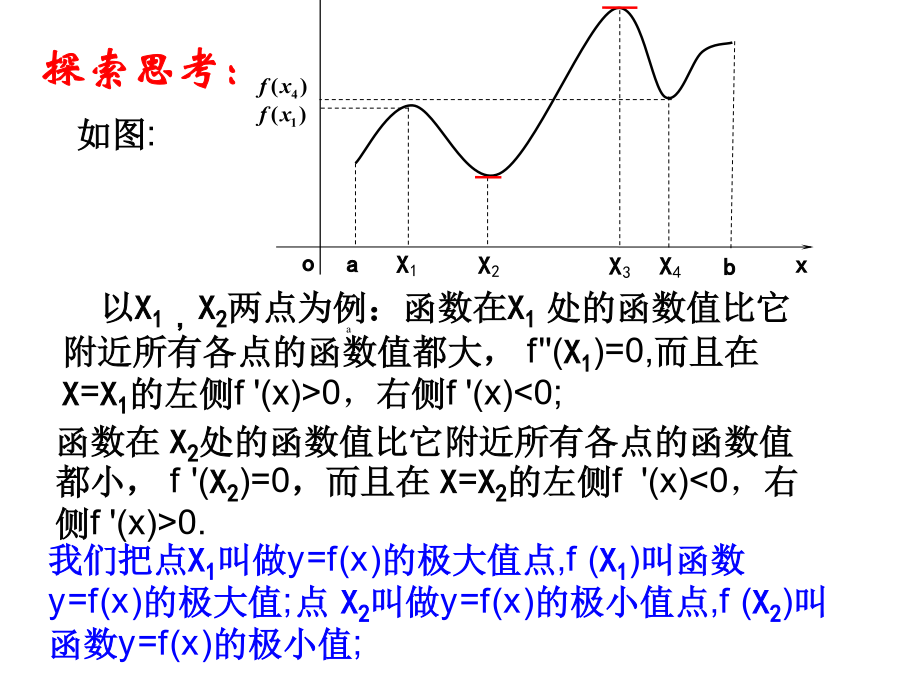
函数的极值与导数2.求函数单调性的一般步骤关注用导数本质及其几何意义解决问题二、新课讲解——函数的极值:从而我们得出结论:若x0满足f/(x)=0,且在x0的两侧的导数异号,则x0是f(x)的极值点,f(x0)是极值,并且如果f/(x)在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果f/(x)在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值.极大值与极小值统称为极值.三、例题选讲:四.探索思考:一般地,求函数y=f(x)的极值的方法是:x练习1:求

2024-08-05

400KB

函数的极值与导数.ppt

1.3.2函数的极值与导数1．了解函数极值的概念，会从几何的角度直观理解函数的极值与导数的关系，并会灵活应用．2．掌握函数极值的判定及求法．3．掌握函数在某一点取得极值的条件．4．增强数形结合的思维意识，提高运用导数的基本思想去分析和解决实际问题的能力．已知y＝f(x)的图象(如图)．[问题1]当x＝a时，函数值f(a)有何特点？[提示1]在x＝a的附近，f(a)最小，f(a)并不一定是y＝f(x)的最小值．[问题2]试分析在x＝a的附近导数的符号．[提示2]在x＝a附近的左侧，曲线的切线斜率小于零，即f

2024-06-06

1.4MB

函数的极值与导数.doc

课题：函数的极值与导数求函数极值的基本步骤：（1）求函数的导数、（2）求解方程、（3）列表判号，即判断在方程的根左，右两边值的符号。例1．求下列函数的极值（1）例2．已知函数.且知当时,取得极大值为7,当时,取得极小值.试求函数的极小值,并求的值.例3.已知函数,在处有极值,且其图象在处的切线与直线平行.求函数的单调区间;（2）求函数的极大值与极小值的差;（3）当时,恒成立,求实数的取值范围.当堂反馈（A）(B)（C）(D)4.已知,若在时有极值.求的值;(2)若函数的图象与函数的图象恰有三个不同的交点,

2024-06-07

93KB