新人教A版高中数学(必修3)31《随机事件的概率》课件二.ppt

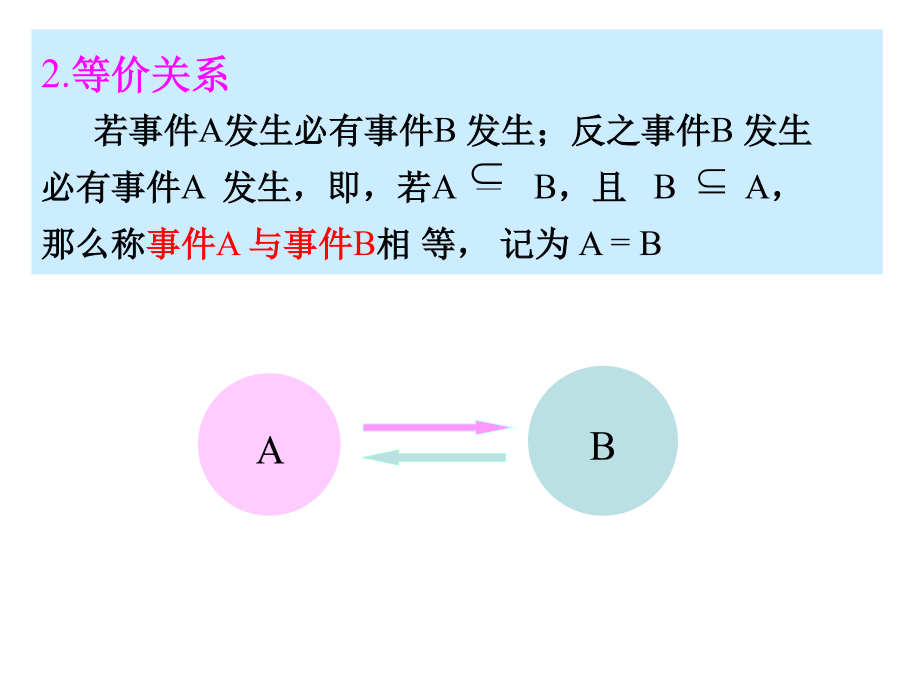
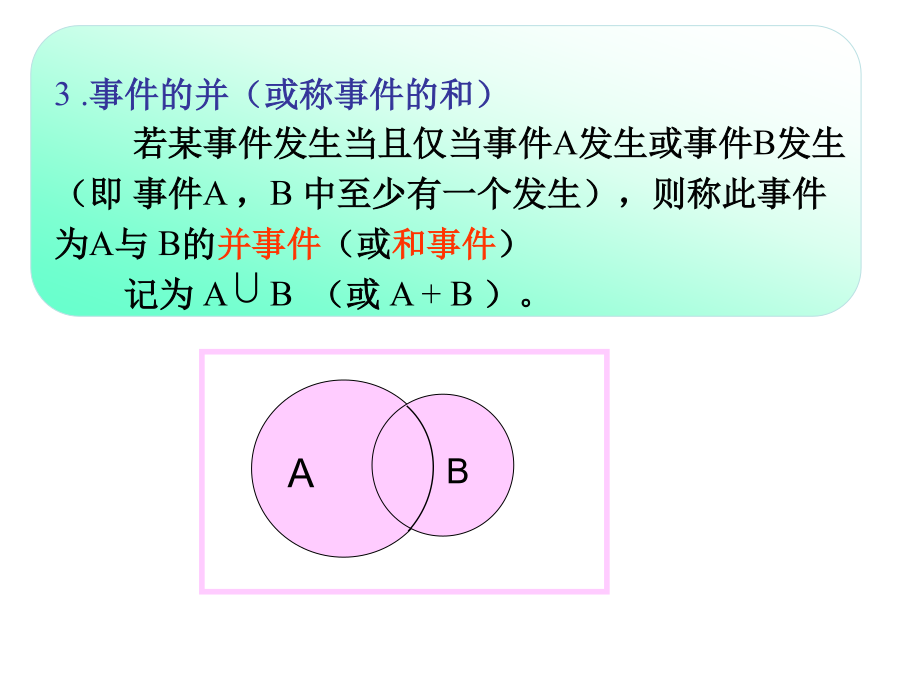
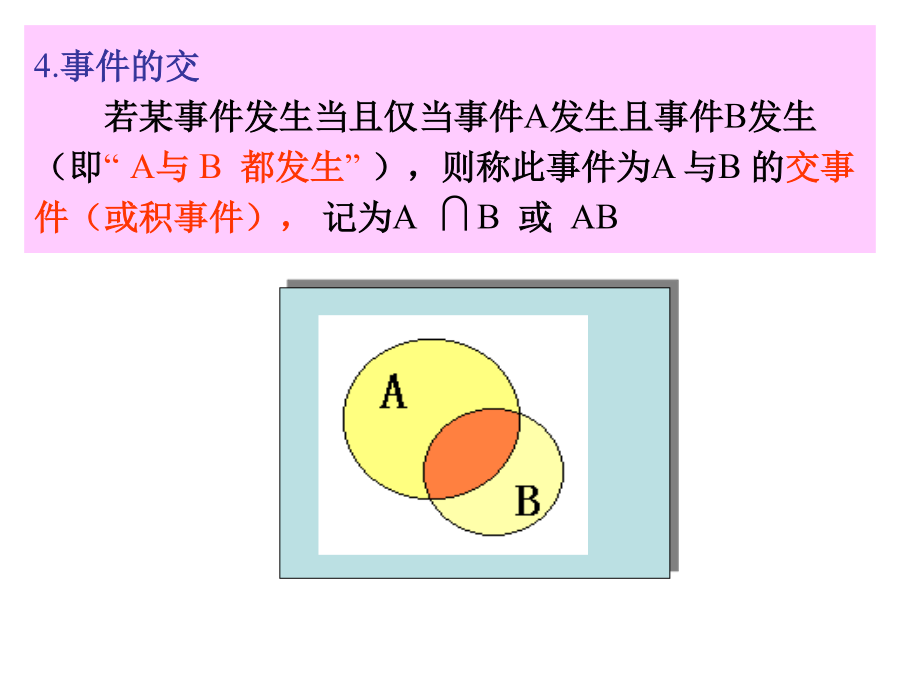
3.1.3概率的基本性质在掷骰子的试验中，我们可以定义许多事件，如：（课本P119）B例：某一学生数学测验成绩记A=95～100分，B=优，说出A、B之间的关系。A显然事件A与事件B等价记为：A=B3.事件的并（或称事件的和）若某事件发生当且仅当事件A发生或事件B发生（即事件A，B中至少有一个发生），则称此事件为A与B的并事件（或和事件）记为AB（或A+B）。显然,事件C,是事件A,B的并记为C=AB4.事件的交若某事件发生当且仅当事件A发生且事件B发生（即“A与B都发生”），则称此事件为A与B的交事件（或积事件），记为AB或AB例：某项工作对视力的要求是两眼视力都在1.0以上。记事件A=“左眼视力在1.0以上”事件B=“右眼视力在1.0以上”事件C=“视力合格”说出事件A、B、C的关系。5.事件的互斥若A∩B为不可能事件（A∩B=），那么称事件A与事件B互斥，其含义是：事件A与B在任何一次试验中不会同时发生。例：抽查一批产品，事件A=“没有不合格品”，事件B=“有一件不合格品”，问这两个事件能否在一次抽取中同时发生。6.对立事件若A∩B为不可能事件，A∪B必然事件，那么称事件A与事件B互为对立事件。其含义是：事件A与事件B在任何一次试验中有且仅有一个发生。例：从某班级中随机抽查一名学生，测量他的身高，记事件A=“身高在1.70m以上”，B=“身高不多于1.7m”说出事件A与B的关系。1、投掷一枚硬币，考察正面还是反面朝上。A={正面朝上}，B={反面朝上}3、一名学生独立解答两道物理习题，考察这两道习题的解答情况。记A=“该学生会解答第一题，不会解答第二题”B=“该学生会解答第一题，还会解答第二题”试回答：1.事件A与事件B互斥吗？为什么？2.事件A与事件B互为对立事件吗？为什么？4、某检查员从一批产品中抽取8件进行检查，观察其中的次品数记：A=“次品数少于5件”;B=“次品数恰有2件”C=“次品数多于3件”;D=“次品数至少有1件”试写出下列事件的基本事件组成：A∪B，A∩C,B∩C;事件的关系和运算二、概率的几个基本性质（2）当事件A与事件B互斥时，A∪B的频率fn(A∪B)=fn(A)+fn(B)由此得到概率的加法公式：如果事件A与事件B互斥，则P（A∪B）=P（A）+P（B）练习：2.甲，乙两人下棋，若和棋的概率是0.5，乙获胜的概率是0.3求：（1）甲获胜的概率；（2）甲不输的概率。3.已知，在一商场付款处排队等候付款的人数及其概率如下：4、抛掷骰子，事件A=“朝上一面的数是奇数”，事件B=“朝上一面的数不超过3”，求P（A∪B）