（浙江专用）高考数学一轮复习 第七章 平面向量 7.2 平面向量的数量积及向量的综合应用课件-人教版高三全册数学课件.pptx

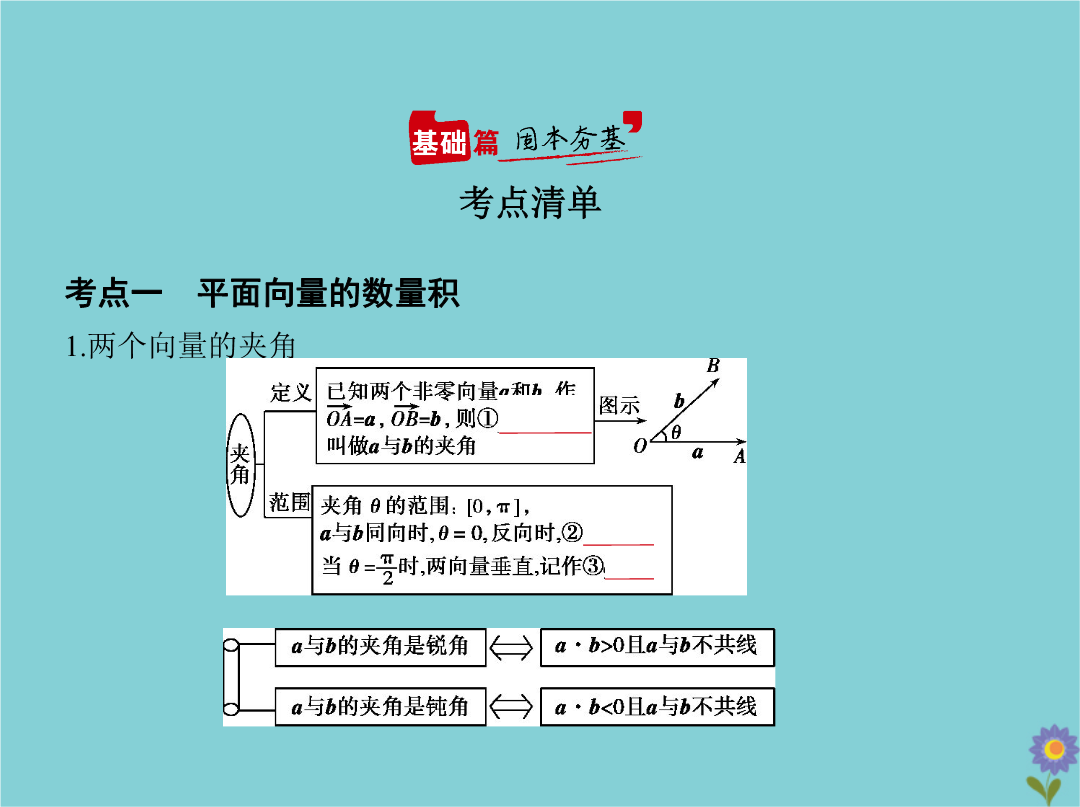
§７.２平面向量的数量积及向量的综合应用考点一平面向量的数量积1.两个向量的夹角 2.平面向量的数量积的有关概念易错警示(1)若abc(b≠0)为实数则ab=bc⇒a=c;但对于向量就不适用即a·b=b·c⇒/a=c.(2)数量积的运算不适合乘法结合律即(a·b)c不一定等于a(b·c).3.平面向量数量积的性质设a、b都是非零向量e是与b方向相同的单位向量θ是a与e的夹角则(1)e·a=a·e=|a|cosθ.(2)a⊥b⇔a·b=⑦0.(3)当a与b同向时a·b=|a||b|;当a与b反向时a·b=-|a||b|.特别地a·a=|a|2;|a|= .(4)cosθ=⑧ .考点二平面向量数量积的应用1.已知a=(x1y1)b=(x2y2)则(1)证明垂直问题常用向量垂直的充要条件:a⊥b⇔a·b=0⇔⑨x1x2+y1y2=0.(2)求夹角问题利用夹角公式:cosθ= =⑩ .(3)求线段的长度可以用向量的线性运算.向量的模|a|= = 或|AB|=| |= .2.向量中常用的结论在△ABC中∠A∠B∠C所对的边分别为abc.(1)在 =λ 的条件下存在λ使得I为△ABC的内心;a +b +c =0⇔P为△ABC的内心.(2)| |=| |=| |⇔P为△ABC的外心.(3) + + =0⇔G为△ABC的重心.(4) · = · = · ⇔P为△ABC的垂心.考法一求向量模的方法解析(1)解法一:由题意知a·b=|a|·|b|·cos60°=2×1× =1则|a+2b|2=(a+2b)2=|a|2+4|b|2+4a·b=4+4+4=12.所以|a+2b|=2 .解法二:根据已知条件建立恰当的坐标系由题意取a=(20)b= 则a+2b=(3 )所以|a+2b|= =2 .(2)∵a=(2-4)b=(-3x)∴2a+b=(1-8+x)又c=(1-1)(2a+b)⊥c∴1+8-x=0则x=9∴b=(-39)∴|b|= =3 故选D.考法二求平面向量夹角的方法解析(1)设2a+b与b的夹角是θ由题意有|2a+b|= =2 (2a+b)·b=2a·b+b2=2|a|·|b|cos +b2=6所以cosθ= = = 所以θ= .(2)设a与a+b的夹角为θ由|a|=|b|得|a|2=|b|2又由|b|=|a-b|得|b|2=|a-b|2则a·b= |a|2∴|a+b|2=|a|2+2a·b+|b|2=3|a|2∴|a+b|= |a|.∴cosθ= = = = .又知θ∈[0π]∴θ= 即a与a+b的夹角为 .例(2019湖南长郡中学第五次月考11)已知P是边长为3的等边三角形ABC外接圆上的动点则| + +2 |的最大值是 ()A.2 B.3 C.4 D.5 解析解法一:设△ABC的外接圆的圆心为O.由正弦定理得圆的半径为 × = .由正三角形的圆心也是其重心得 + + =0故 + +2 =4 + .|4 + |≤|4 |+| |=5R=5 当且仅当 与 同向即PC为圆O直径时取得最大值5 .解法二:设O为△ABC外接圆的圆心以O为圆心OA所在直线为y轴过O与OA垂直的直线为x轴建立平面直角坐标系如图所示 连接OBOC.易知| |=| |=| |= ∴A(0 )B C 设P( cosθ sinθ)(0≤θ<2π).则 =(- cosθ - sinθ) =  = ∴ + +2 = ∴| + +2 |=