（天津专用）高考数学大一轮复习 5.2 平面向量数量积与应用课件-人教版高三全册数学课件.pptx

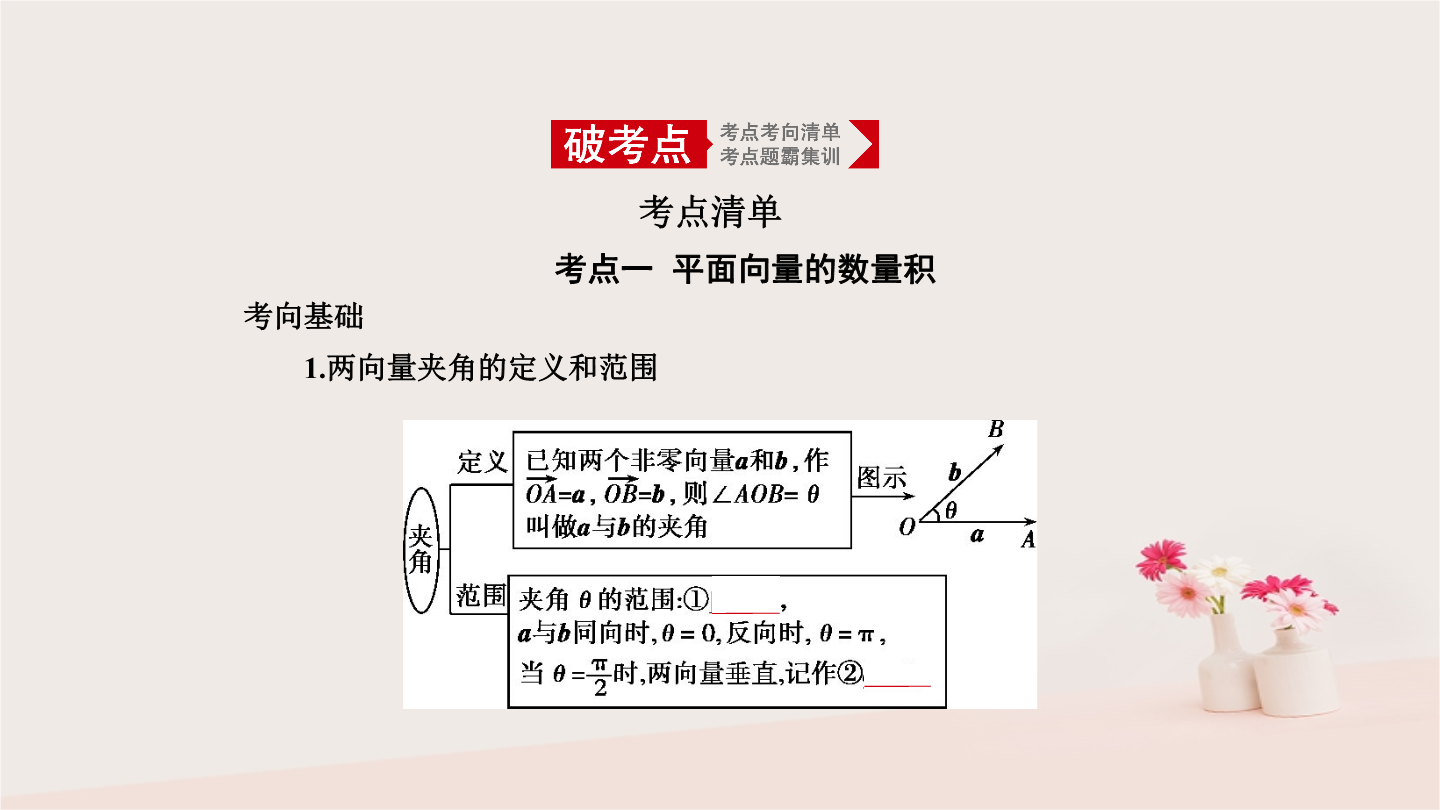
考点一平面向量的数量积 3.向量数量积的性质设ab都是非零向量e是与b方向相同的单位向量θ是a与e的夹角则(1)e·a=a·e=⑤|a|·cosθ.(2)当a与b同向时⑥a·b=|a||b|;当a与b反向时⑦a·b=-|a||b|.考向突破考点二平面向量数量积的应用2.向量中常用的结论在△ABC中∠A∠B∠C所对的边分别为abc.(1)在 =λ 的条件下存在λ使得I为△ABC的内心;a +b +c =0⇔P为△ABC的内心.(2)| |=| |=| |⇔P为△ABC的外心.(3) + + =0⇔G为△ABC的重心.(4) · = · = · ⇔P为△ABC的垂心.考向突破 = = 其中sinφ= cosφ= .显然当sin(α+φ)=1时| + + |取得最大值 = +1.解法二: + + = + + + 设a= + + =(2 )则|a|=  + + =a+ 则| + + |=|a+ |≤|a|+| |= +1考向二求向量的夹角解析(1)∵(a-b)⊥(3a+2b)∴(a-b)·(3a+2b)=0⇒3|a|2-a·b-2|b|2=0⇒3|a|2-|a|·|b|·cos<ab>-2|b|2=0.又∵|a|= |b|∴ |b|2- |b|2·cos<ab>-2|b|2=0.∴cos<ab>= .∵<ab>∈[0π]∴<ab>= .选A.(2)由题意不妨设e1=(10)e2=(01)则 e1-e2=( -1)e1+λe2=(1λ).根据向量的夹角公式得cos60°= = = 所以 -λ= 解得λ= .考向三向量垂直的条件方法1求平面向量的模的方法1.把几何图形放到适当的坐标系中写出有关向量的坐标求向量的模.如若向量a=(xy)求向量a的模只需利用公式|a|= 即可.2.当向量的坐标无法表示时利用向量的线性运算和向量的数量积公式进行求解关键是会把向量a的模进行如下转化:|a|= .例1平面向量a与b的夹角为45°a=(11)|b|=2则|3a+b|等于 ()A.13+6 B.2 C. D. 解题导引 方法2求平面向量的夹角的方法1.定义法:利用向量数量积的定义知cosθ= 其中两个向量的夹角θ∈[0π]求解时应求出三个量:a·b|a||b|或找出这三个量之间的关系.2.坐标法:若a=(x1y1)b=(x2y2)θ为ab的夹角则cosθ= .3.三角函数法:可以把所求两向量的夹角放到三角形中利用正、余弦定理和三角形的面积公式等内容进行求解.例2(2015重庆75分)已知非零向量ab满足|b|=4|a|且a⊥(2a+b)则a与b的夹角为 ()A. B. C. D. 解题导引 方法3用向量法解决平面几何问题的方法1.用向量法解决平面几何问题的基本步骤:①建立平面几何与向量的联系用向量表示问题中涉及的几何元素将平面几何问题转化为向量的问题;②通过向量运算研究几何元素之间的关系如距离、夹角等问题;③把运算结果转化成几何关系.2.用向量法解平面几何问题主要是通过建立平面直角坐标系将问题坐标化然后利用平面向量的坐标运算求解有关问题这样可以避免繁杂的逻辑推理同时加强了数形结合思想在解题中的应用.例3在△ABC和△AEF中B是EF的中点AB=EF=1BC=6CA= 若 · + · =2则 与 的夹角的余弦值为.