高考数学二轮复习 专题三 立体几何 第3讲 立体几何中的向量方法课件 理-人教版高三全册数学课件.pptx

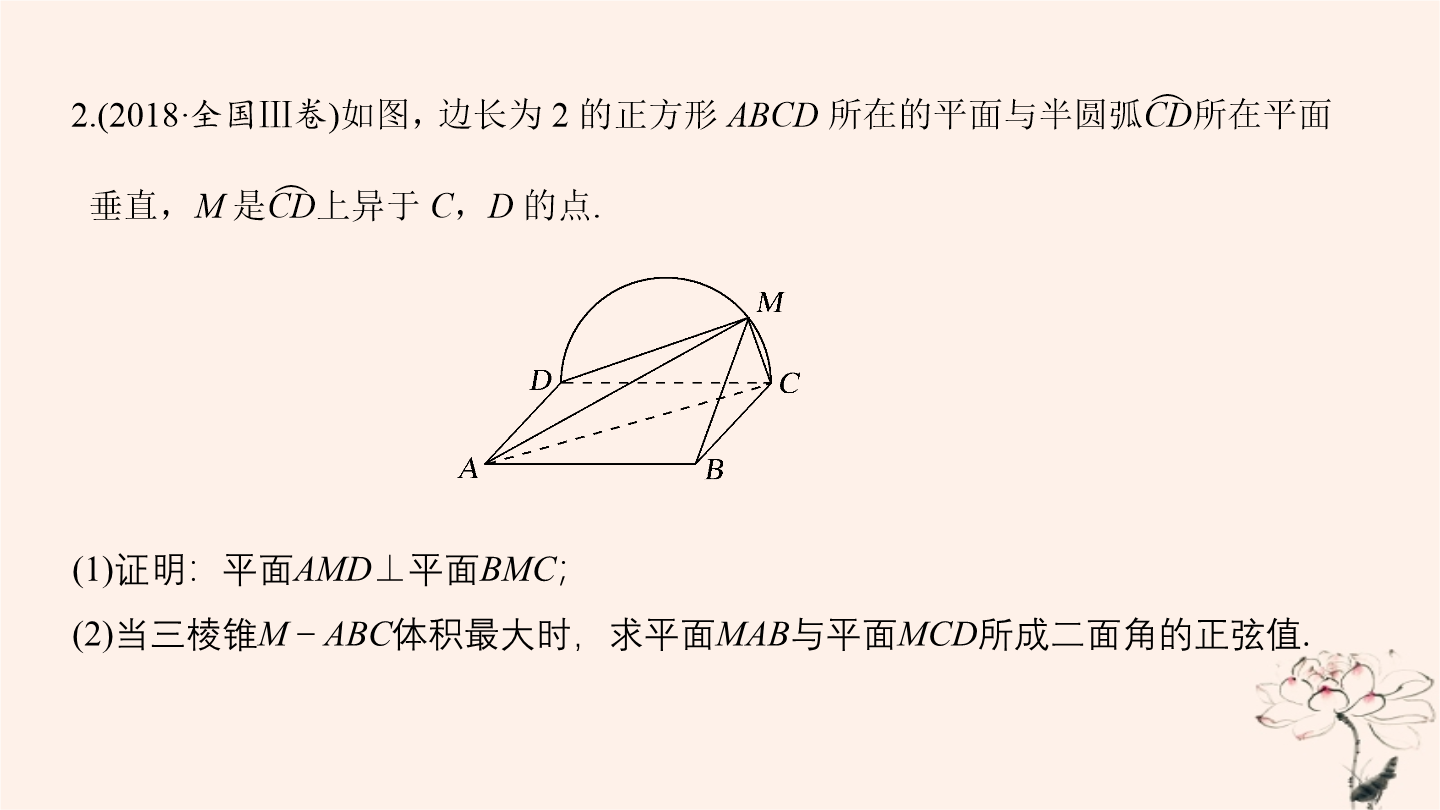
第3讲立体几何中的向量方法高考定位以空间几何体为载体考查空间角是高考命题的重点常与空间线面关系的证明相结合热点为二面角的求解均以解答题的形式进行考查难度主要体现在建立空间直角坐标系和准确计算上.1.(2017·全国Ⅱ卷)已知直三棱柱ABC－A1B1C1中∠ABC＝120°AB＝2BC＝CC1＝1则异面直线AB1与BC1所成角的余弦值为()则B(000)B1(001)C1(101).在△ABC中AC2＝AB2＋BC2－2AB·BC·cos∠ABC(1)证明：平面AMD⊥平面BMC；(2)当三棱锥M－ABC体积最大时求平面MAB与平面MCD所成二面角的正弦值.(1)证明由题设知平面CMD⊥平面ABCD交线为CD.因为BC⊥CDBC⊂平面ABCD所以BC⊥平面CMD又DM⊂平面CDM故BC⊥DM.由题设得D(000)A(200)B(220)C(020)M(011)3.(2018·全国Ⅰ卷)如图四边形ABCD为正方形EF分别为ADBC的中点以DF为折痕把△DFC折起使点C到达点P的位置且PF⊥BF.(1)证明：平面PEF⊥平面ABFD；(2)求DP与平面ABFD所成角的正弦值.(2)解作PH⊥EF垂足为H.由(1)得PH⊥平面ABFD.1.直线与平面、平面与平面的平行与垂直的向量方法2.直线与直线、直线与平面、平面与平面的夹角计算热点一利用空间向量证明平行、垂直关系【例1】如图在四棱锥P－ABCD中PA⊥底面ABCDAD⊥ABAB∥DCAD＝DC＝AP＝2AB＝1点E为棱PC的中点.证明：证明依题意以点A为原点建立空间直角坐标系(如图)(2)因为AB⊥AD又PA⊥平面ABCDAB⊂平面ABCD所以AB⊥PAPA∩AD＝APAAD⊂平面PAD所以AB⊥平面PAD设平面PCD的一个法向量为n＝(xyz)探究提高1.利用向量法证明平行、垂直关系关键是建立恰当的坐标系(尽可能利用垂直条件准确写出相关点的坐标进而用向量表示涉及到直线、平面的要素).2.向量证明的核心是利用向量的数量积或数乘向量但向量证明仍然离不开立体几何定理的条件如在(2)中忽略BE⊄平面PAD而致误.【训练1】在直三棱柱ABC－A1B1C1中∠ABC＝90°BC＝2CC1＝4点E在线段BB1上且EB1＝1DFG分别为CC1C1B1C1A1的中点.求证：(1)B1D⊥平面ABD；(2)平面EGF∥平面ABD.则B1D⊥BAB1D⊥BD.又BA∩BD＝BBABD⊂平面ABD因此B1D⊥平面ABD.热点二利用空间向量计算空间角考法1求线面角或异面直线所成的角【例2－1】(2018·烟台质检)如图在梯形ABCD中AD＝BCAB∥CDAC⊥BD平面BDFE⊥平面ABCDEF∥BDBE⊥BD.(1)证明∵平面BDFE⊥平面ABCD平面BDFE∩平面ABCD＝BDAC⊂平面ABCDAC⊥BD∴AC⊥平面BDFE.又AC⊂平面AFC∴平面AFC⊥平面BDFE.则B(020)D(0－10)F(002)C(－100)探究提高1.异面直线所成的角θ可以通过两直线的方向向量的夹角φ求得即cosθ＝|cosφ|.2.直线与平面所成的角θ主要通过直线的方向向量与平面的法向量的夹角φ求得即sinθ＝|cosφ|有时也可分别求出斜线与它在平面内的射影直线的方向向量转化为求两方向向量的夹角(或其补角).【训练2】(2018·江苏卷)如图在正三棱柱ABC－A1B1C1中AB＝AA1＝2点PQ分别为A1B1BC的中点.(1)求异面直线BP与AC1所成角的余弦值；(2)求直线CC1与平面AQC1所成角的正弦值.因为AB＝AA1＝2设n＝(xyz)为平面AQC1的一个法向量(1)证明：BC⊥B1M；(2)若平面MB1C把此棱柱分成体积相等的两部分求此时二面角M－B1C－A的余弦值.∴BC＝2则有AB2＋BC2＝8＝AC2∴∠ABC＝90°∴BC⊥AB又∵BB1⊥BCBB1∩AB＝B∴BC⊥平面ABB1A1又B1M⊂平面ABB1A1故BC⊥B1M.(2)解由题设知平面MB1C把此三棱柱分成两个体积相等的几何体为四棱锥C－ABB1M和四棱锥B1－A1MCC1.∴A(200)C(020)B1(004)M(202).探究提高1.二面角的大小可以利用分别在两个半平面内与棱垂直的直线的方向向量的夹角(或其补角)或通过二面角的两个面的法向量的夹角求得它等于两个法向量的夹角或其补角.2.利用向量法求二面角必须能判定“所求二面角的平面角是锐角或钝角”否则解法是不严谨的.(1)求证：AC⊥平面BEF；(2)求二面角B－CD－C1的余弦值；(3)证明：直线FG与平面BCD相交.(1)证明在三棱柱ABC－A1B1C1中因为CC1⊥平面ABC所以四边形A1ACC1为矩形.又EF分别为ACA1C