等腰梯形、中位线.doc

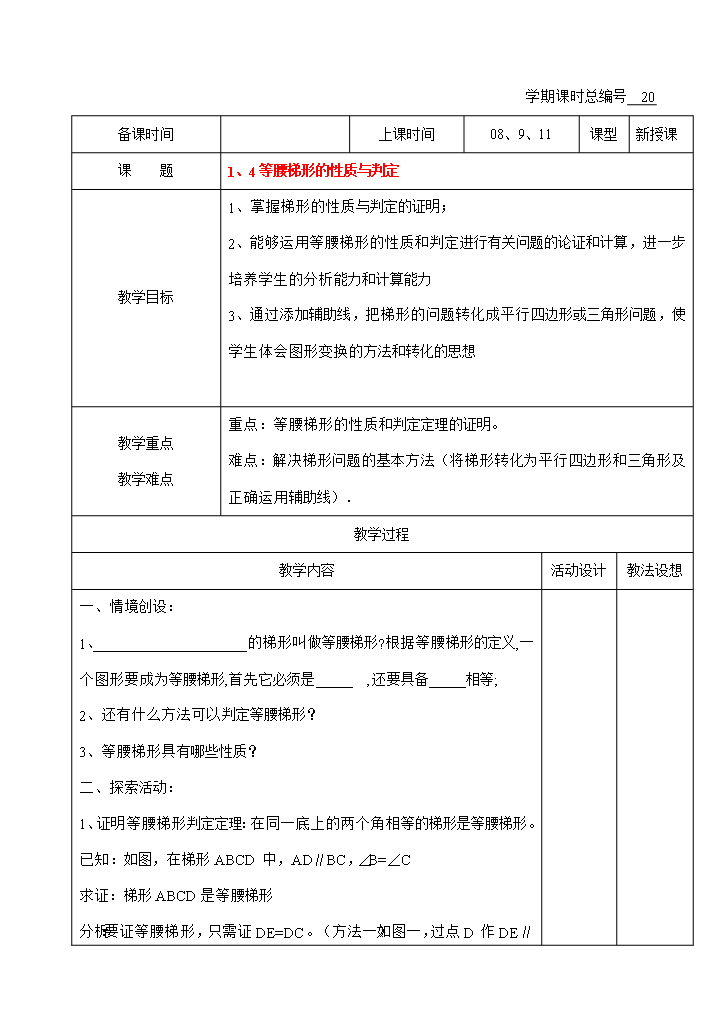
学期课时总编号20备课时间上课时间08、9、11课型新授课课题1、4等腰梯形的性质与判定教学目标1、掌握梯形的性质与判定的证明；2、能够运用等腰梯形的性质和判定进行有关问题的论证和计算进一步培养学生的分析能力和计算能力3、通过添加辅助线把梯形的问题转化成平行四边形或三角形问题使学生体会图形变换的方法和转化的思想教学重点教学难点重点：等腰梯形的性质和判定定理的证明。难点：解决梯形问题的基本方法（将梯形转化为平行四边形和三角形及正确运用辅助线）．教学过程教学内容活动设计教法设想一、情境创设：1、_____________________的梯形叫做等腰梯形?根据等腰梯形的定义一个图形要成为等腰梯形首先它必须是_____还要具备_____相等;2、还有什么方法可以判定等腰梯形？3、等腰梯形具有哪些性质？二、探索活动：1、证明等腰梯形判定定理：在同一底上的两个角相等的梯形是等腰梯形。已知：如图在梯形ABCD中AD∥BC∠B=∠C求证：梯形ABCD是等腰梯形分析：要证等腰梯形只需证DE=DC。（方法一）如图一过点D作DE∥AB并交BC于E得∠DEC=∠B=∠C所以得DE=DC；（方法二）如图二作高AE、DF通过证Rt△ABE≌Rt△DCF得出AB=DC；（方法三）如图三分别延长BA、CD交于点E则△EAD与△EBC都是等腰三角形所以可得结论。思考：你会证明这个定理是否存在逆定理？怎样证明？2、求证：等腰梯形的两条对角线相等已知：在梯形ABCD中AD∥BCAB=DC。求证：AC=BD。分析：要证AC=BD只要用等腰梯形的性质得出∠ABC=∠DCB然后再利用△ABC≌△DCB即可得出AC=BD。3、小结解决梯形问题常用的添加辅助线的方法（1）“作高”：使两腰在两个直角三角形中；（4）“延腰”：构造具有公共角的两个等腰三角形；（2）“移腰”：使两条腰在同一个三角形中；（3）“移对角线”：使两条对角线在同一个三角形中；（5）“等积变形”：连结梯形一底的一端点和另一腰中点并延长与另一底延长线交于一点构成全等三角形。三、例题精讲：例1：如图在直角梯形ABCD中AB∥DC∠ABC=900AB=2DC对角线AC⊥BD垂足为F过点F作EF∥AB交AD于点ECF=4㎝。（1）求证：四边形ABFE是等腰梯形；（2）求AB的长。例2：如图已知在梯形ABCD中AD∥BCAB=DC对角线AC和BD相交于点OE是BC边上的一个动点（点E不于B、C两点重合）EF∥BD交AC于点F。EG∥AC交BD于点G。（1）、求证：四边形EFOG的周长等于2OB；（2）、请将上述题目的条件“梯形ABCD中AD∥BCAB=DC”改为另一种四边形其他条件不变使得结论“四边形EFOG的周长等于2OB”仍成立并将改编后的题目画出图形写出已知、求证不必证明。四、巩固练习：1、如图已知梯形ABCD中AD∥BCAB=CD=ADACBD相交于O点∠BCD=60°则下列说法正确的是（）A．梯形ABCD是轴对称图形B．BC=2AD（1）（2）C．梯形ABCD是中心对称图形D．AC平分∠DCB2、如图(1)是一个等腰梯形由6个这样的等腰梯形恰好可以拼出如图(2)所示的一个菱形．对于图(1)中的等腰梯形请写出它的内角的度数或腰与底边长度之间关系的一个正确结论：3、在梯形中∥若点为线段上任意一点（与、不重合）．问：当点在什么位置时画出图形并说明理由．4、已知：如图在梯形ABCD中AD∥BCBC=DCCF平分∠BCDDF∥ABBF的延长线交DC于点E。求证：（1）△BFC≌△DFC（2）AD=DE小结思考：研究四边形问题常常把它转化成研究三角形的问题这就把一个有待解决的新问题转化为我们会解的问题。A类尝试题：课时作业感受理解：1、2、3、4、5、6、巩固题：课时作业思考运用：7、8、10拓展题：拓展探究：9创新题：B类尝试题：课时作业感受理解：1、2、3、4、5、6巩固题：课时作业思考运用7、8拓展题：创新题：拓展探究9教后反思目标达成评估需改进的问题1.4等腰梯形的性质与判定一、引入新课：1、_____________________的梯形叫做等腰梯形?根据等腰梯形的定义一个图形要成为等腰梯形首先它必须是_____还要具备_____相等;2、还有什么方法可以判定等腰梯形？3、等腰梯形具有哪些性质？