
高中数学:2.2《直线与平面平行、平面与平面平行的判定》新人教版必修2A.doc

安双****文章



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

高中数学:2.2《直线与平面平行、平面与平面平行的判定》新人教版必修2A.doc
用心爱心专心2.2.1-2.2.2直线与平面平行的判定、面面平行的判定一、教学目标:1、知识与技能(1)理解并掌握直线与平面平行的判定定理;平面与平面平行的判定定理。(2)进一步培养学生观察、发现的能力和空间想象能力;2、过程与方法学生通过观察图形借助已有知识掌握直线与平面平行的判定定理。3、情感、态度与价值观(1)让学生在发现中学习增强学习的积极性;(2)让学生了解空间与平面互相转换的数学思想。二、教学重点、难点重点、难点:直线与平面平行的判定定理、平面与平面平行的判定定理及应用。三

直线与平面平行的判定平面与平面平行的判定.doc
2.2.1《直线与平面平行的判定平面与平面平行的判定》导学案【学习目标】知识与技能:理解并掌握直线与平面平行的判定定理及平面与平面平行的判定定理.过程与方法:掌握由“线线平行”证得“线面平行”的数学证明思想。进一步熟悉反证法;进一步培养观察能力、空间想象力和类比、转化能力,提高逻辑推理能力。情感态度价值观:培养认真、仔细、严谨的学习态度。建立“实践―理论―再实践”的科学研究方法。【重点难点】学习重点:掌握直线与平面平行的判定定理.掌握平面与平面平行的判定定理.学习难点:理解直线与平面平行的判定定理.理解平
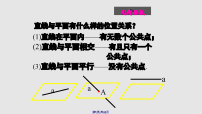
直线与平面平行平面与平面平行判定.pptx
复习引入讲授新课讲授新课符号表示:A练习3.判断命题的真假求证:空间四边形相邻两边的中点的连线平行于经过另外两边所在的平面定理的应用________________.变式2变式2变式2巩固练习如图.M,N分别是AB,PC的中点定义:如果两个平面没有公共点,那么这两个平面互相平行,也叫做平行平面.若平面内有一条直线与平面平行,那么,平行吗?若平面内有一条直线与平面平行,那么,平行吗?若平面内有一条直线与平面平行,那么,平行吗?平面与平面平行的判定定理平面与平面平行的判定定理1.、

直线与平面平行的判定222平面与平面平行的判定.ppt
2.2直线、平面平行的判定及其性质2.2.1直线与平面平行的判定2.2.2平面与平面平行的判定当门扇绕着一边转动时,转动的一边与门框所在的平面是怎样的位置关系呢?活动板房各个面是怎样拼在一起的,它们都有什么关系呢?木工师傅用气泡式水准仪在桌面上交叉放两次,如果水准仪的气泡都是居中的,就可以判定这个桌面和水平面平行,这是什么道理?1.理解直线与平面平行的判定定理.(重点)2.会用判定定理证明简单的线面平行的问题.(难点)3.理解并掌握两平面平行的判定定理及其应用.(重点、难点)4.进一步培养学生观察、发现的

高中数学《直线与平面平行的判定》教案人教版必修2A.doc
用心爱心专心威坪中学课时授课计划授课时间:___年__月___日星期:授课教师:课题2.2.1直线与平面平行的判定课时第课时课型新授课授课班级课时教学目标(1)理解并掌握直线与平面平行的判定定理;(2)掌握转化的思想“线线平行线面平行”教学重点、难点重点:直线与平面平行的判定定理及应用难点:直线与平面平行的判定定理及应用教学方法实验用具及教具教学过程设计教师教学活动设计学生活动设计一、复习准备:1、直线与平面有哪几种位置关系?(用长方体模型进行演示)(1)直线与平面平行;(2)直线与平面相交;(3)直线在
