
§2.4 线性回归方程(2).doc

是丹****ni



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

§2.4 线性回归方程(2).doc
用心爱心专心No.______用案时间:____月_____日用案人:__________课题§2.4线性回归方程(2)教学目标(1)了解非确定性关系中两个变量的统计方法;(2)掌握散点图的画法及在统计中的作用;(3)掌握回归直线方程的求解方法重难点线性回归方程的求解.回归直线方程在现实生活与生产中的应用方法及教具教学过程备注一、复习练习1.三点的线性回归方程是(D)ABCD2.我们考虑两个表示变
§2.4 线性回归方程(1).doc
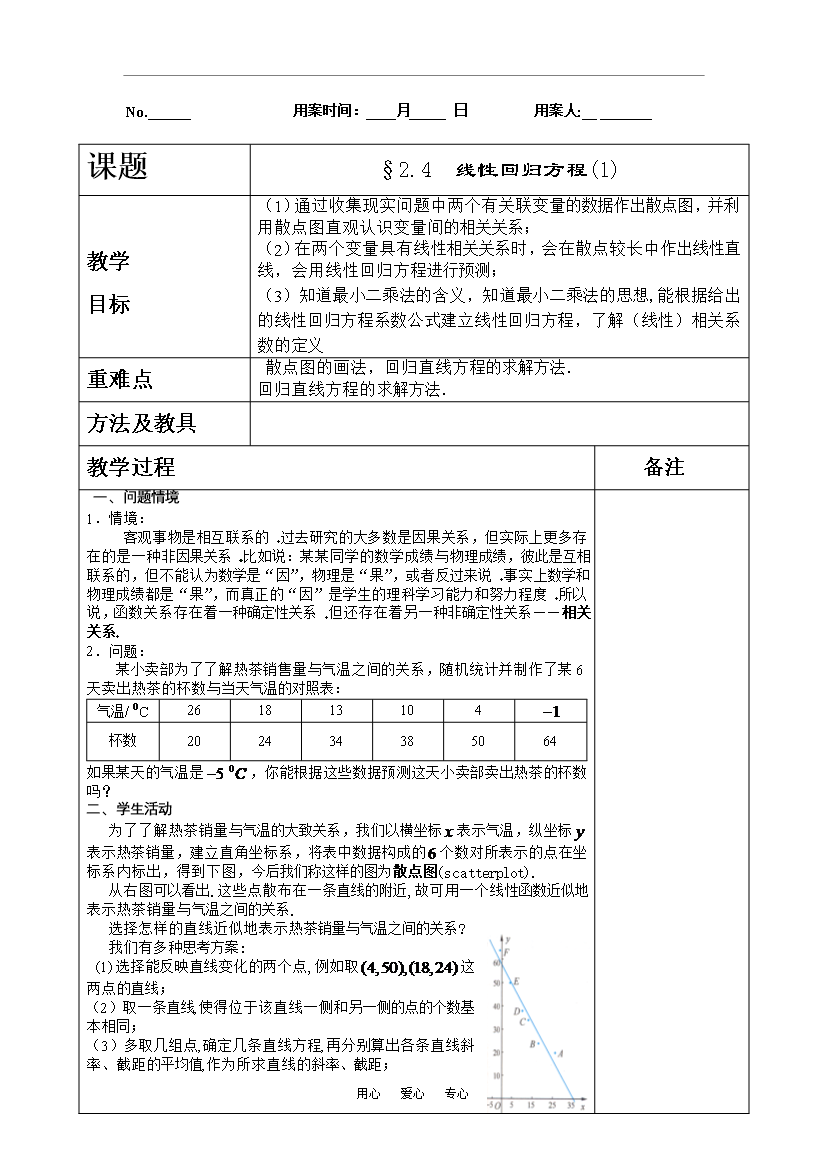
用心爱心专心No.______用案时间:____月_____日用案人:_________课题§2.4线性回归方程(1)教学目标(1)通过收集现实问题中两个有关联变量的数据作出散点图并利用散点图直观认识变量间的相关关系;(2)在两个变量具有线性相关关系时会在散点较长中作出线性直线会用线性回归方程进行预测;(3)知道最小二乘法的含义知道最小二乘法的思想能根据给出的线性回归方程系数公式建立线性回归方程了解(线性)相关系数的定义重难点散点图的画

《2.4线性回归方程》导学案.doc
《2.4线性回归方程》导学案学习目标:了解非确定性关系中两个变量的统计方法;掌握散点图的画法及在统计中的作用,掌握回归直线方程的求解方法。学习重难点:了解非确定性关系中两个变量的统计方法学习过程:解析视屏:1.相关关系的概念在实际问题中,变量之间的常见关系有两类:一类是确定性函数关系,变量之间的关系可以用函数表示。例如正方形的面积S与其边长之间的函数关系(确定关系);一类是相关关系,变量之间有一定的联系,但不能完全用函数来表达。例如一块农田的水稻产量与施肥量的关系(非确定关系)相关关系:自变量取值一定时,

(第10课时)§2.4 线性回归方程(2).doc
东台市富安中学高二数学教学案东台市富安中学高二数学教学案2普通高中课程标准实验教科书—数学必修三[苏教版]普通高中课程标准实验教科书—数学必修三[苏教版](第10课时)§2.4线性回归方程(2)教学目标(1)了解非确定性关系中两个变量的统计方法;(2)掌握散点图的画法及在统计中的作用;(3)掌握回归直线方程的求解方法.教学重点线性回归方程的求解.教学难点回归直线方程在现实生活与生产中的应

高中数学:2.4 线性回归方程(2)(苏教版必修3).doc
用心爱心专心2.4线性回归方程(2)教学目标(1)了解非确定性关系中两个变量的统计方法;(2)掌握散点图的画法及在统计中的作用;(3)掌握回归直线方程的求解方法.教学重点线性回归方程的求解.教学难点回归直线方程在现实生活与生产中的应用.教学过程一、复习练习1.三点的线性回归方程是(D)ABCD2.我们考虑两个表示变量与之间的关系的模型为误差项模型如下:模型1:;模型2:.(1)如果分别求两个模型中的值;(2)分别说明以上两个模型是确定性模型还是随机
