
高一数学:3.1.2《用二分法求方程的近似解》教案新人教A版必修1.doc

论文****可爱





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

数学:3.1.2《用二分法求方程的近似解》(新人教A版必修1).pptx
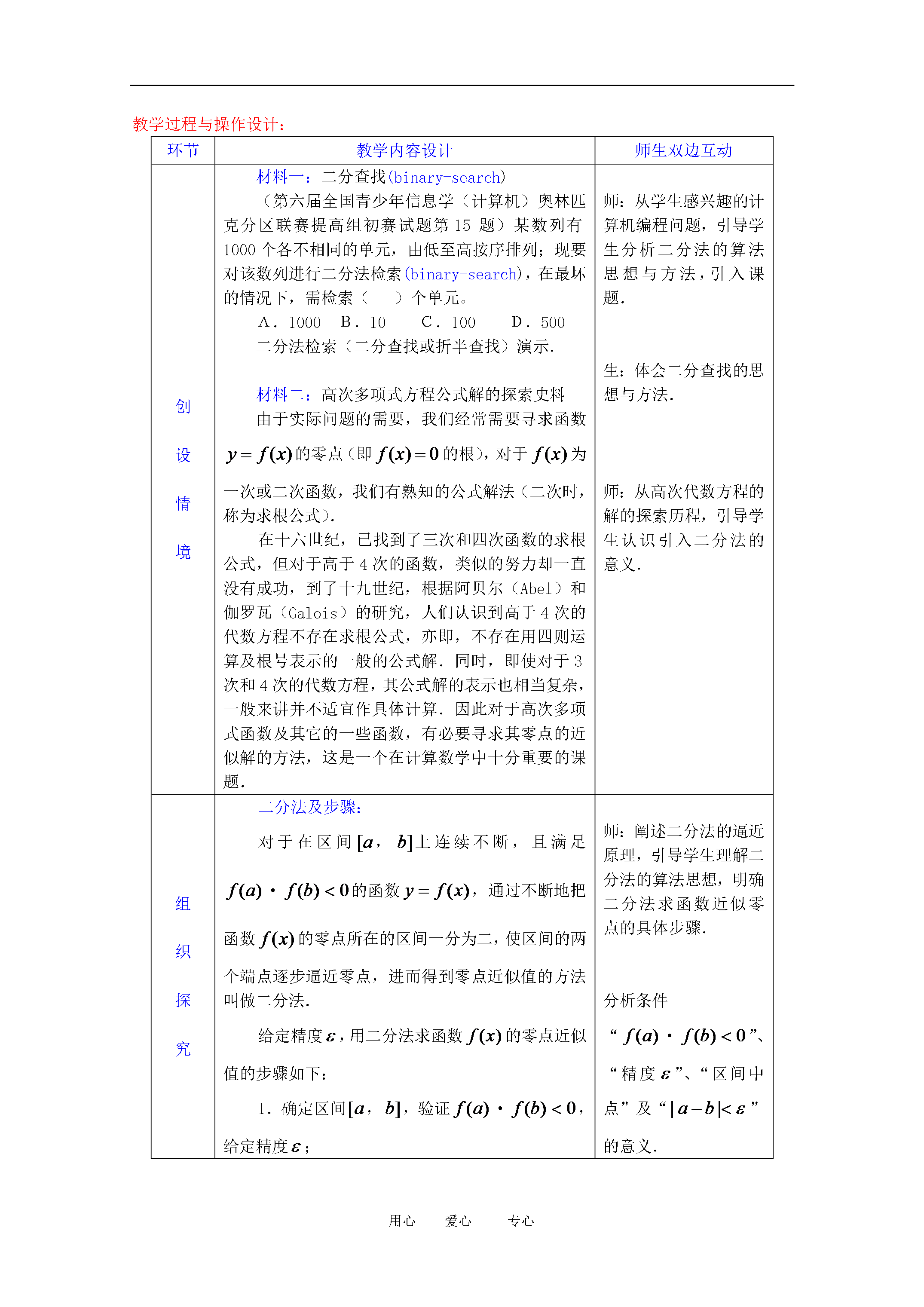
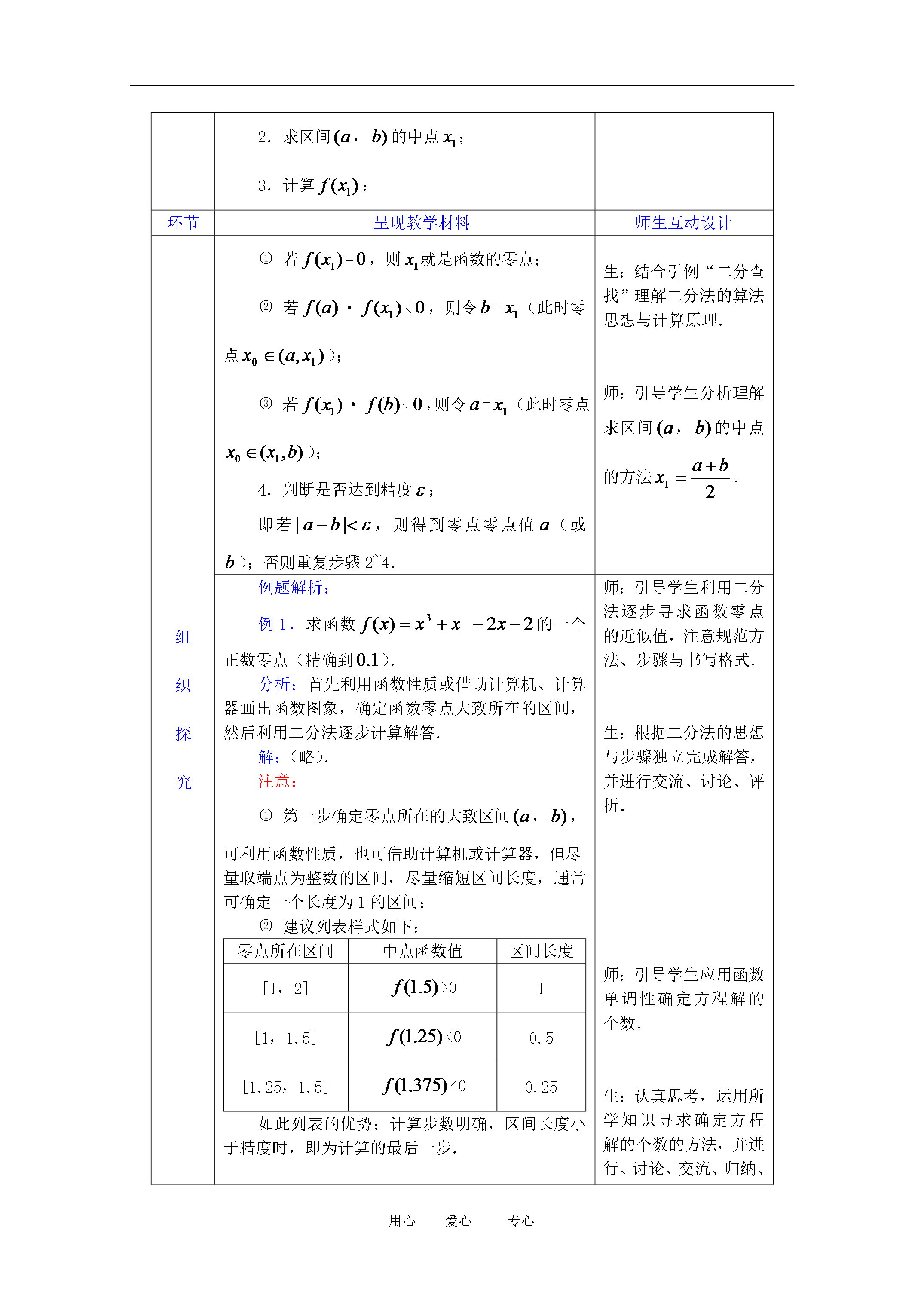
会计学复习思考:对于方程(1),可以利用一元二次方程的求根公式求解,但对于(2)的方程,我们却没有公式可用来求解.模拟实验室模拟实验室模拟实验室模拟实验室模拟实验室模拟实验室模拟实验室模拟实验室模拟实验室所以x=2.53125为函数f(x)=lnx+2x-6在区间(2,3)内的零点近似值,也即方程lnx=-2x+6的近似解x1≈2.53。给定精确度,用二分法求函数零点x0的步骤:周而复始怎么办?精确度上来判断.练习:/生活中也常常会用到二分法思想:答案:

高一数学:3.1.2《用二分法求方程的近似解》教案新人教A版必修1.doc
用心爱心专心课题:§3.1.2用二分法求方程的近似解教学目标:知识与技能通过具体实例理解二分法的概念及其适用条件了解二分法是求方程近似解的常用方法从中体会函数与方程之间的联系及其在实际问题中的应用.过程与方法能借助计算器用二分法求方程的近似解并了解这一数学思想为学习算法做准备.情感、态度、价值观体会数学逼近过程感受精确与近似的相对统一.教学重点:重点通过用二分法求方程的近似解体会函数的零点与方程根之间的联系初步形成用函数观点处理问题的意识.难点恰当地使用信息技术工具利

3.1.2《用二分法求方程的近似解》(新人教A版必修1).ppt
函数的应用3.1函数与方程3.1.2用二分法求方程的近似解A级:1、了解二分法是求方程近似解的常用方法;2、能用二分法求方程的近似解。B级:1、理解二分法求函数零点近似值的步骤;2、能借助计算器或计算机用二分法求方程的近似解。C级:1、理解函数与方程之间的联系;2、能用函数与方程思想分析问题、解决问题。A、学习重点:1、用二分法求方程的近似解;2、体会函数的零点与方程的根之间的联系。B、学习难点:借助信息技术工具,用二分法求给定精确度的方程的近似解。1.函数的零点中央电视台有一档娱乐节目“幸运52”,主持

高一数学教案:3.1.2《用二分法求方程的近似解》新人教A版必修1.doc
用心爱心专心课题:§3.1.2用二分法求方程的近似解教学目标:知识与技能通过具体实例理解二分法的概念及其适用条件了解二分法是求方程近似解的常用方法从中体会函数与方程之间的联系及其在实际问题中的应用.过程与方法能借助计算器用二分法求方程的近似解并了解这一数学思想为学习算法做准备.情感、态度、价值观体会数学逼近过程感受精确与近似的相对统一.教学重点:重点通过用二分法求方程的近似解体会函数的零点与方程根之间的联系初步形成用函数观点处理问题的意识.难点恰当地使用信息技术工具利

高中数学 3.1.2《用二分法求方程的近似解1》教案 新人教A版必修1.doc
3专心爱心用心教学过程设计一、问题情境设疑问题:函数在区间(23)内有零点如何找出这个零点?解决:策略一:用几何画板画出函数的图象求出其与x轴交点的横坐标也可以求函数与函数y=6–2x的图象交点的横坐标。游戏:请你模仿李咏主持一下幸运52请同学们猜一下下面这部手机的价格。思考:如何做才能以最快的速度猜出它的价格?合作探究:利用我们猜价格的方法你能否求解方程lnx+2x–6=0?如果能求解的话怎么去解?你能用函数的零点的性质吗?策略二:“取中点”逐步缩小零点所在的范围——二
