高中数学 3.1.2《用二分法求方程的近似解》课件 新人教A版必修1.ppt

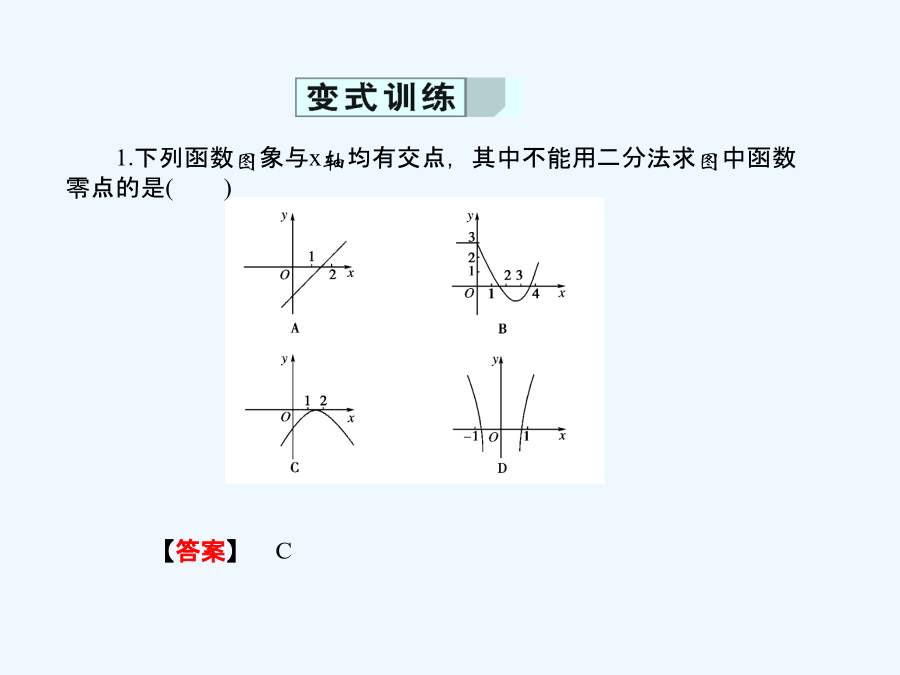
3.1.2用二分法求方程的近似解(3)计算f(c)；①若f(c)＝0，则；②若f(a)·f(c)<0，则令b＝c(此时零点x0∈；③若f(c)·f(b)<0，则令a＝c(此时零点x0∈．(4)判断a，b是否达到精确度ε：即若|a－b|<ε，则得到零点近似值a(或b)；否则重复(2)～(4)．【解析】利用二分法求函数零点必须满足零点两侧函数值异号．在B中，不满足f(a)·f(b)<0，不能用二分法求零点，由于A、C、D中零点两侧函数值异号，故可采用二分法求零点．故选B.【答案】B1.下列函数图象与x轴均有交点，其中不能用二分法求图中函数零点的是()【解析】作出y＝lgx，y＝3－x的图象可以发现，方程lgx＝3－x有唯一解，记为x0，并且解在区间(2,3)内．区间3.求函数f(x)＝x3＋x2－2x－2的一个为正数的零点(精确度为0.1)．【解析】由于f(1)＝－2<0，f(2)＝6>0，可取区间(1,2)作为计算的初始区间．用二分法逐步计算，列表如下：由上表计算可知区间(1.375,1.438)长度小于0.1，故可在(1.438,1.5)内取1.4065作为函数f(x)正数的零点的近似值．2．用二分法求函数零点近似值的注意点(1)在第一步中要使：①区间[a，b]的长度尽量小；②f(a)、f(b)的值比较容易计算，且f(a)·f(b)<0.(2)二分法仅对函数变号零点(即零点两侧某区域内函数值异号)适用．(3)根据函数的零点与相应方程根的关系，求函数的零点与求相应方程的根是等价的．对于求方程f(x)＝g(x)的根，可以构造函数F(x)＝f(x)－g(x)，函数F(x)的零点即为方程f(x)＝g(x)的根．f(2.25)＝0.0625，因为f(2.2)·f(2.25)<0，所以x0∈(2.2,2.25)，同理可得x0∈(2.225,2.25)，(2.225,2.2375)，又f(2.225)≈－0.0494，f(2.2375)≈0.0064，且|0.0064－(－0.0494)|＝0.0558<0.1，所以原方程的近似正解可取为2.225.【错因】本题错解的原因是对精确度的理解不正确，精确度ε满足的关系式为|a－b|<ε，而本题错解中误认为是|f(a)－f(b)|<ε.【正解】令f(x)＝x2－5，因为f(2.2)＝－0.16<0，f(2.4)＝0.76>0，所以f(2.2)·f(2.4)<0，说明这个函数在区间(2.2,2.4)内有零点x0，取区间(2.2,2.4)的中点x1＝2.3，f(2.3)＝0.29，因为f(2.2)·f(2.3)<0，所以x0∈(2.2,2.3)，再取区间(2.2,2.3)的中点x2＝2.25，f(2.25)＝0.0625，因为f(2.2)·f(2.25)<0，所以x0∈(2.2,2.25)，由于|2.25－2.2|＝0.05<0.1，所以原方程的近似正解可取为2.25.课时作业点击进入链接