
概率论与数理统计-等可能概型-古典概型PPT幻灯片课件.ppt

可爱****乐多








亲,该文档总共43页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

概率论与数理统计-等可能概型-古典概型PPT幻灯片课件.ppt
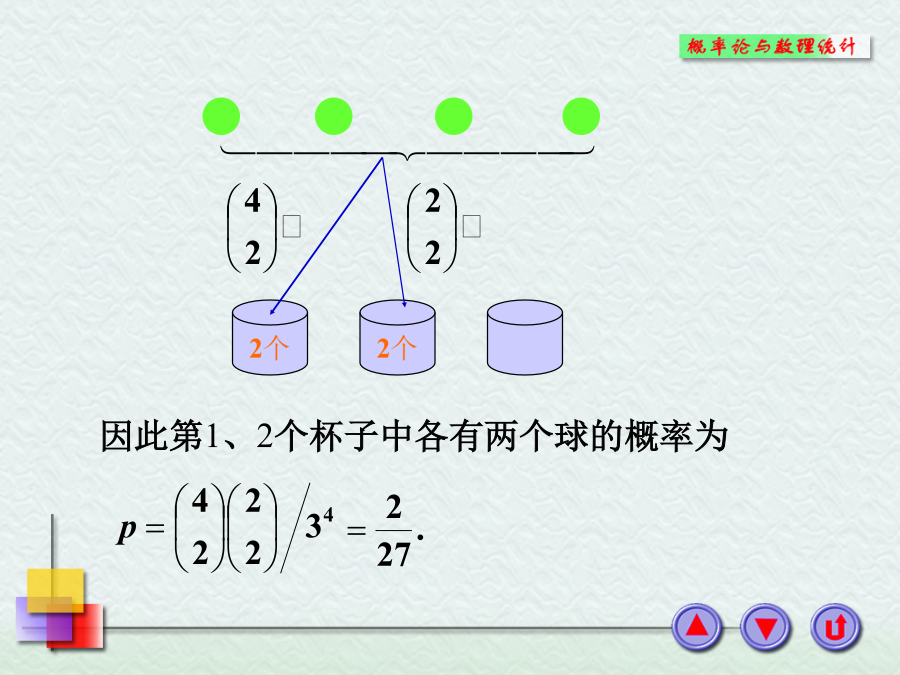
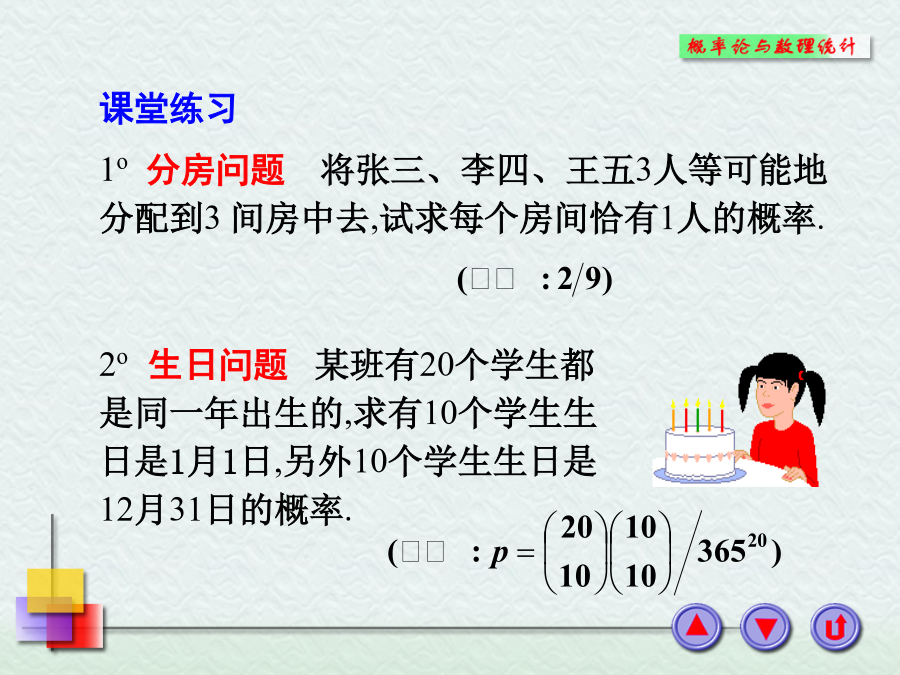
一、等可能概型1.定义设试验E的样本空间由n个样本点构成,A为E的任意一个事件,且包含m个样本点,则事件A出现的概率记为:3.古典概型的基本模型:摸球模型(2)有放回地摸球基本事件总数为4.古典概型的基本模型:球放入杯子模型(2)每个杯子只能放一个球2o生日问题某班有20个学生都是同一年出生的,求有10个学生生日是1月1日,另外10个学生生日是12月31日的概率.解例2(3)取到的两只球中至少有一只是白球的概率.可利用(4.1)式来计算事件的概率.得例3假设每人的生日在一年365天中任一天是等可64个人的

概率论与数理统计等可能概型古典概型ppt课件.ppt
一、等可能概型1.定义设试验E的样本空间由n个样本点构成,A为E的任意一个事件,且包含m个样本点,则事件A出现的概率记为:3.古典概型的基本模型:摸球模型(2)有放回地摸球基本事件总数为4.古典概型的基本模型:球放入杯子模型(2)每个杯子只能放一个球2o生日问题某班有20个学生都是同一年出生的,求有10个学生生日是1月1日,另外10个学生生日是12月31日的概率.解例2(3)取到的两只球中至少有一只是白球的概率.可利用(4.1)式来计算事件的概率.得例3假设每人的生日在一年365天中任一天是等可64个人的

概率论与数理统计课件1.3古典概型与几何概型.pptx
§1.3古典概型与几何概型一、等可能概型(古典概型)概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计二.几何概型概率论与数理统计概率论与数理统计概率论与数理统计概率论与数理统计

浙大概率论与数理统计课件 概率1-4等可能概型(古典概型).ppt
第四节等可能概型(古典概型)我们首先引入的计算概率的数学模型,是在概率论的发展过程中最早出现的研究对象,通常称为称这种试验为等可能随机试验或古典概型.例4设有N件产品,其中有M件次品,现从这N件中任取n件,求其中恰有k件次品的概率.历年考题:“等可能性”是一种假设,在实际应用中,我们需要根据实际情况去判断是否可以认为各基本事件或样本点是等可能的.在许多场合,由对称性和均衡性,我们就可以认为基本事件是等可能的并在此基础上计算事件的概率.3、许多表面上提法不同的问题实质上属于同一类型:(2)有n个人,设每个人

概率论与数理统计12 古典概型和几何概型.ppt
1.2古典概型和几何概型例1.9一只口袋装有6只球,其中4只白球,2只红球设A表示事件“取到的两只球都是白球”B表示事件“取到的两只球颜色相同”C表示事件“取到的两只球至少一只是白球的概率”(a)有放回抽取(b)不放回抽取二、几何概型:因而几何概型的等可能性是通过下列方式给出其确切作业
