数学建模教案市公开课一等奖百校联赛特等奖课件.pptx

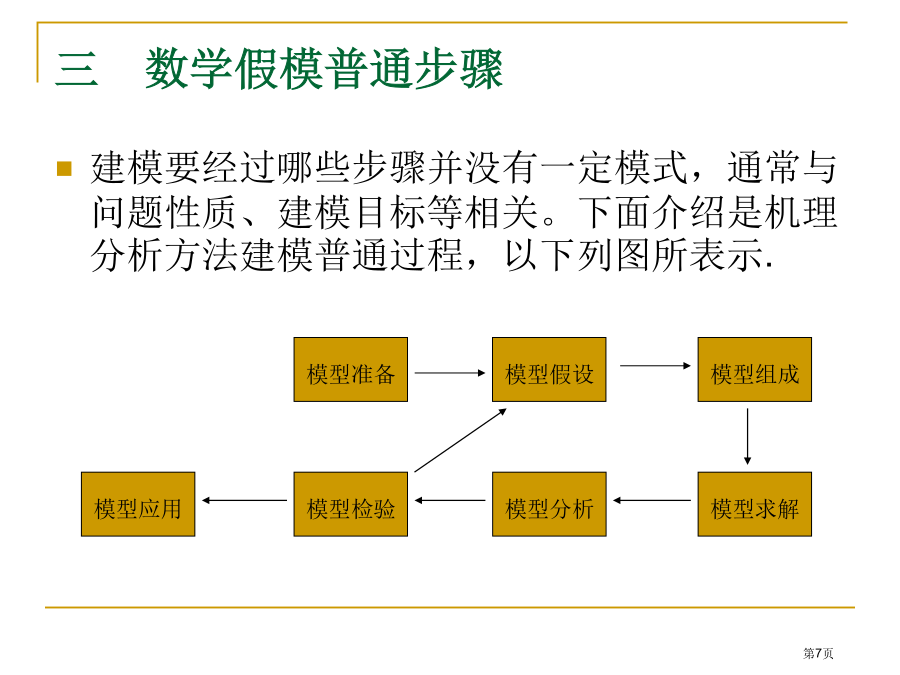
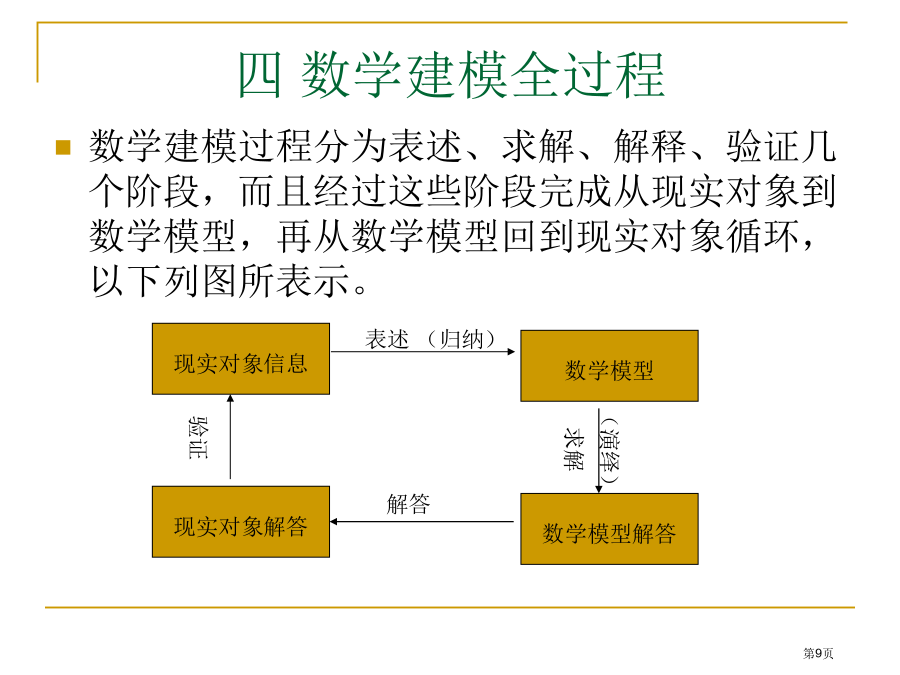
数学建模教案序言一数学建模和数学关系数学建模定义:数学建模是指用数学语言和方法对实际问题进行近似地刻划和描述，数学建模并不是新事物，自从有了数学并用数学去处理问题时，就有了数学建模。纵观人类历史上进行过三次重大科学技术革命，每一次都是渗透着数学应用，都是数学建模过程。但将数学建模作为一门专门学科和课程历史还很短。数学建模教学培养目标:1培养翻译能力2应用已学到数学方法和思想进行综合应用和分析，并能学习一点新数学知识，并能了解合理抽象和简化，尤其是进行数学分析主要性3发展联想能力4逐步发展形成一个洞察力5熟练使用技术伎俩数学理论二数学建模竞赛（MCM）由来和规则三数学假模普通步骤模型准备了解问题实际背景，明确建模目标，搜集必要信息如现象、数据等，尽可能搞清对象主要特征形成一个比较清楚“问题”，由此初步确定用哪一类模型。情况明才能方法对。在模型准备阶段要深入调查研究，虚心向实际工作者请教，尽可能掌握第一手资料。模型假设依据对象特征和建模目标，抓住问题本质，忽略次要原因，作出必要、合理简化假设。对于建模成败这是非常主要和困难一步。假设作不合理或太简单，会造成错误或无用模型；假设作得过分详细，试图把复杂对象众多原因都考虑进去，会使你极难或无法继续下一部工作。经常需要再合理与简化之间作出恰当折衷。模型组成依据所作假设，用数学语言、符号描述对象内在规律，建立包含常量、变量等数学模型，如优化模型、微分方程模型、差分方程模型、图模型等。建模时应遵照一个标准是：尽可能采取简单数学工具，因为你模型总希望更多人了解和使用，而不是只供少数教授观赏。模型求解能够采取解方程、画图形、优化方法、数值计算、统计分析等各种数学方法，尤其是数学软件和计算机技术。模型分析对求解结果进行数学上分析，如结果误差分析、统计分析、模型对数据敏感性分析、对假设健壮性分析等。模型检验把求解和分析结果翻译回到实际问题，与实际现象、数据比较，检验模型合理性和适用性。假如结果与实际不符，问题经常出在模型假设上，应该修改、补充假设，重新建模，如图中虚线所表示。这一步对于模型是否真有用非常关键，要以严厉认真态度对待。有些模型要经过几次重复，不停完善，直到检验结果取得某种程度上满意。模型应用应用方式与问题性质、建模目标及最终结果相关，本课程普通不讨论这个问题。数学建模过程分为表述、求解、解释、验证几个阶段，而且经过这些阶段完成从现实对象到数学模型，再从数学模型回到现实对象循环，以下列图所表示。表述是将现实问题“翻译”成抽象数学问题，属于归纳法。数学模型求解则属于演绎法。归纳是依据个别现象推出一般规律；演绎是按照普遍原理考查特定对象，导出结论。因为任何事物本质都要经过现象来反映，必然要透过偶然来表露，所以正确归纳不是主观、盲目，而是有客观基础，但也往往是不精细、带感性，不易直接检验其正确性。演绎利用严格逻辑推理，对解释现象、作出科学预见具有重大意义，但是它要以归纳结论作为公理化形式前提，只能在这个前提下保证其正确性。所以，归纳和演绎是辨证统一过程：归纳是演绎基础，演绎是归纳指导。解释是把数学模型解答“翻译”回到现实对象，给出分析、预报、决策或者控制结果。最后，作为这个过程重要一环，这些结果需要用实际信息加以验证。上图揭示了现实对象和数学模型关系。一方面，数学模型是将现象加以归纳、抽象产物，它源于现实，又高于现实。其次，只有当数学建模结果经受住现实对象检验时，才可以用来知道实际，完成实践——理论——实践这一循环。五数学模型特点和建模能力培养直觉和灵感在数学建模中往往也起着不可忽略作用。直觉是人们对新事物本质极敏锐领悟、了解或推断，灵感指在人们有意识或下意识思索过程中迸发出来猜测、思绪或判断。二者都含有突发性，且思维者本人往往说不清它来路和道理。当因为各种限制利用已经有知识难以对研究对象作出有效推理和判断时，凭借相同、类比、猜测，外推等思维方式及不完整、不连续、不严密，带启发性直觉和灵感，去“战略性”地认识对象，是人类创造性思维特点之一，也是人脑比按程序逻辑工作计算机、机器人高明之处。直觉和灵感不是凭空产生，它要求人们含有丰富背景知识，对问题进行重复思索和艰难探索对各种思维方法利用娴熟。相互讨论和思想交锋，尤其是不一样专业组员之间探讨，是激发直觉和灵感主要原因。掌握建模这门艺术，培养想象力和洞察力，需要作好这么两条：第一，学习、分析、评价、改造他人作过模型。首先弄懂它，分析为何这么作，然后找出它优缺点，并尝试改进方法。第二，要亲自动手，踏实地做几个实际题目。为了这个目标，本课程主要将采取实例研究方法。第一章初等模型问题１跑步问题某人在任何5min时间区间内均不能恰好跑500m，问10min内能否恰好跑1000m。问题３商人过河问题三名商人各带一个随从乘船过河，一只小船只能容纳两人，有他们自己划