2-线性规划问题的图解法.pdf

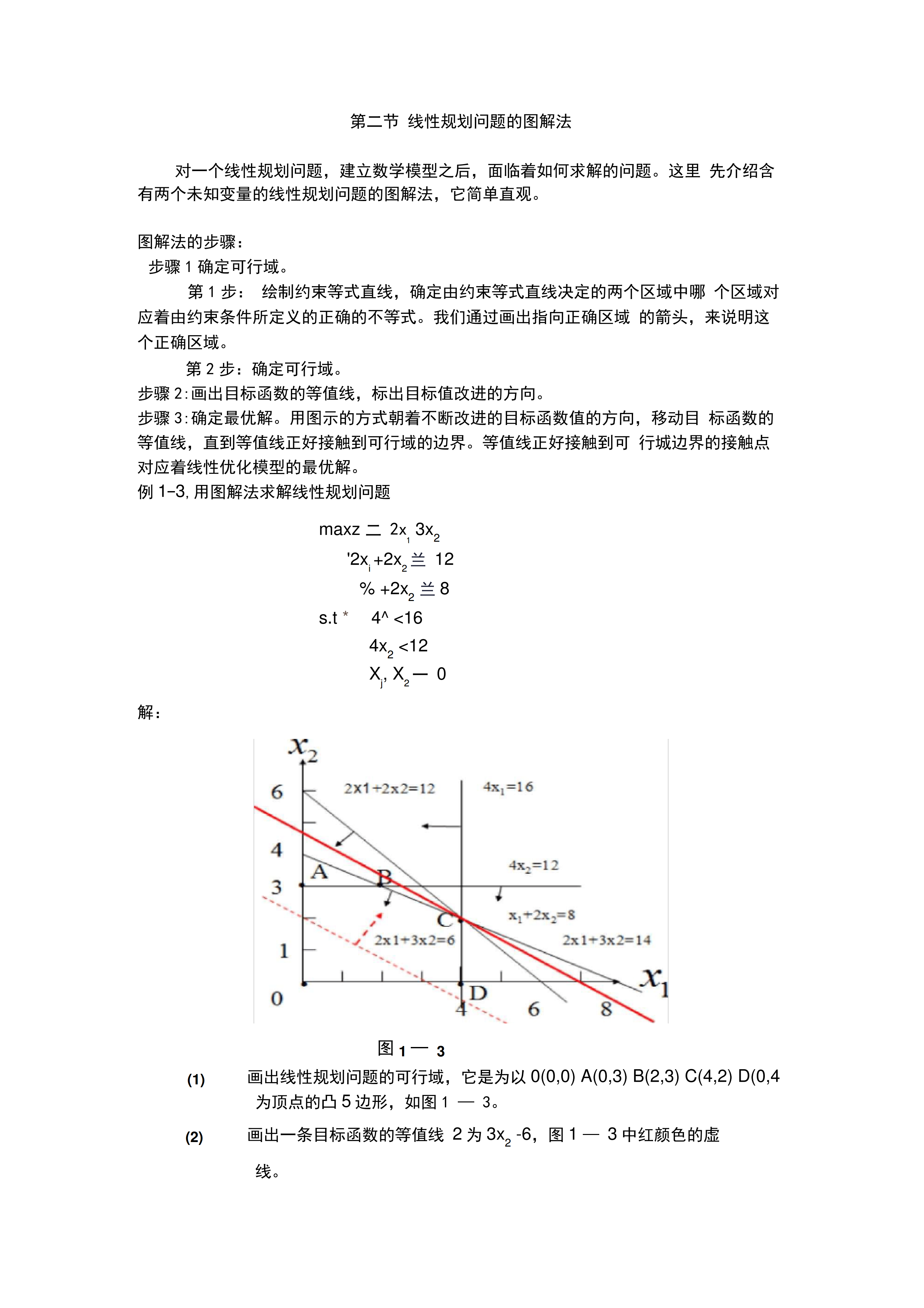
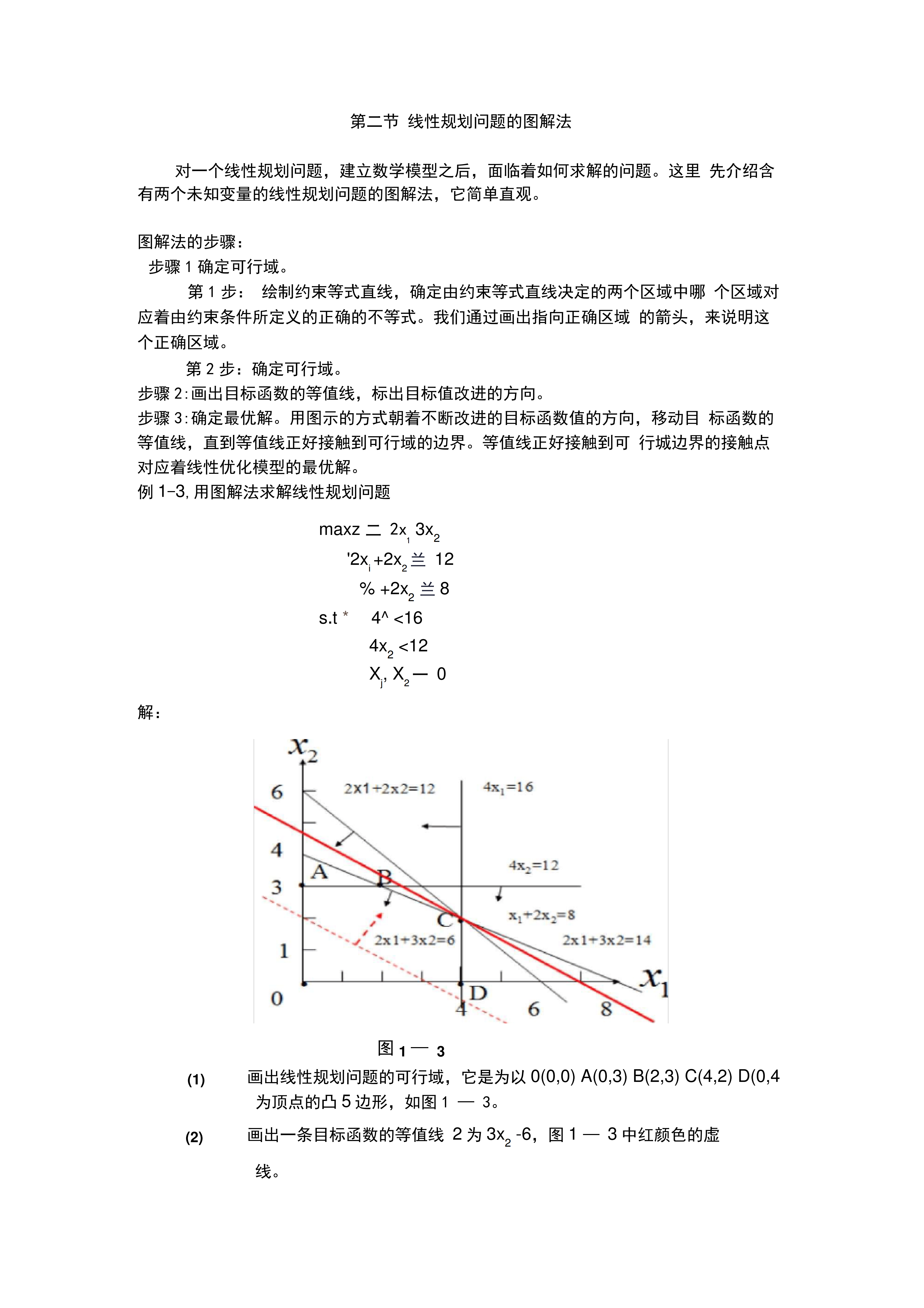
第二节线性规划问题的图解法对一个线性规划问题，建立数学模型之后，面临着如何求解的问题。这里先介绍含有两个未知变量的线性规划问题的图解法，它简单直观。图解法的步骤：步骤1确定可行域。第1步：绘制约束等式直线，确定由约束等式直线决定的两个区域中哪个区域对应着由约束条件所定义的正确的不等式。我们通过画出指向正确区域的箭头，来说明这个正确区域。第2步：确定可行域。步骤2:画出目标函数的等值线，标出目标值改进的方向。步骤3:确定最优解。用图示的方式朝着不断改进的目标函数值的方向，移动目标函数的等值线，直到等值线正好接触到可行域的边界。等值线正好接触到可行城边界的接触点对应着线性优化模型的最优解。例1-3,用图解法求解线性规划问题maxz二2x3x12'2x+2x兰12i2%+2x兰82s.t*4^<164x<122X,X一0j2解：图1—3(1)画出线性规划问题的可行域，它是为以0(0,0)A(0,3)B(2,3)C(4,2)D(0,4为顶点的凸5边形，如图1—3。画出一条目标函数的等值线2为3x-6，图1—3中红颜色的虚(2)2线。(3)目标函数的等值线往上移动时，目标函数值增大（图1—3中红颜色的实线）。由于问题的解要满足全部约束条件，因此目标函数的等值线要与可行域有交点。当目标函数的等值线移动到2\3x=14时，它与可行域只有一个交点，再往上移动时，与2可行域不再有交点。这就是说最优解为：x^4,x^2，最优目标]2函数值为14。例1-3中求解得到问题的最优解是唯一的，但对一般线性规划问题，求解结果还可能出现以下几种情况：（1）唯一最优解（2）多重最优解。（3）无界解。（4）无可行解。这里我们不再举例，请大家自己阅读教材。当线性规划问题的求解结果出现（3）、（4）两种情况时，一般说明线性规划问题建模有错误。前者缺乏必要的约束条件，后者是有矛盾的约束条件，建模时应注意。