
2 线性规划的图解法.ppt

qw****27








亲,该文档总共33页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

§2 线性规划的图解法.ppt
图解法线性规划问题求解的几种可能结果由图解法得到的启示例1的数学模型9—8—7—6—5—4—3—2—1—09—8—7—6—5—4—3—2—1—09—8—7—6—5—4—3—2—1—09—8—7—6—5—4—3—2—1—09—8—7—6—5—4—3—2—1—0图解法求解步骤线性规划问题求解的几种可能结果(b)无穷多最优解(c)无界解MaxZ=x1+x2-2x1+x24x1-x22x1、x20(d)无可行解MaxZ=2x1+3x2x1+2x284x1164x212-2x1+x24x1、x20可

2 线性规划的图解法.ppt
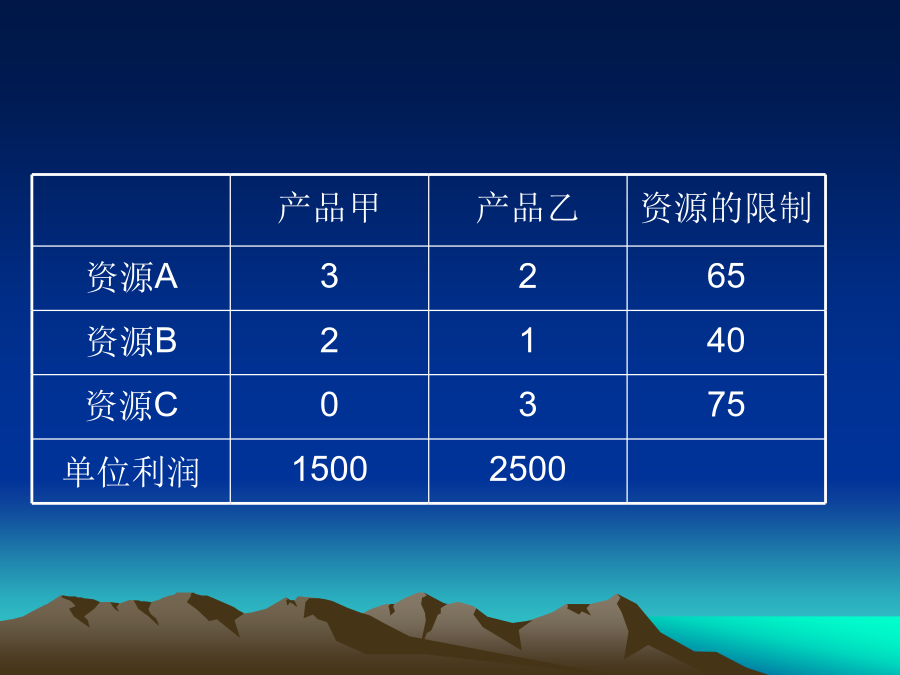
运筹帷幄之中◇学习重点及难点1、线性规划问题的建模及图解法(熟练掌握)2、图解法的求解过程及解的各种情况(重点)3、图解法的灵敏度分析(熟练掌握)第二章线性规划的图解法§1线性规划问题及其数学模型例1.资源的合理利用问题解:将一个实际问题转化为线性规划模型有以下几个步骤:1.确定决策变量:设x1表示生产甲产品的数量;x2表示生产乙产品的数量2.确定目标函数:工厂的目标是总利润最大maxz=1500x1+2500x23.确定约束条件:3x1+2x265(A资源的限制)2x1+x240(B资源的限制)3x

第2章__线性规划的图解法.ppt
第二章线性规划的图解法线性规划问题的提出线性规划的基本概念线性规划的数学模型线性规划问题的标准形式问题的提出产品I决策变量(Decisionvariables)目标函数(Objectivefunction)约束条件(Constraintconditions)可行域(Feasibleregion)最优解(Optimalsolution)是问题中要确定的未知量,表明规划中的用数量表示的方案、措施,可由决策者决定和控制。第2步--定义目标函数MaxZ=50x1+100x2对我们有何限制?第3步--表示约束条件该

第2章__线性规划的图解法.pptx
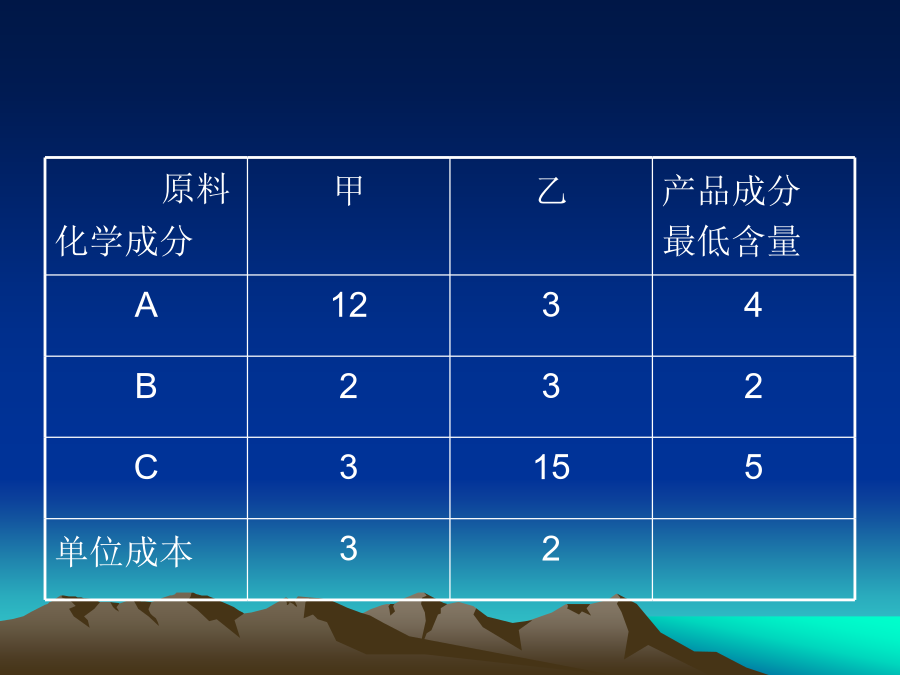
会计学问题的提出决策变量(Decisionvariables)目标函数(Objectivefunction)约束条件(Constraintconditions)可行域(Feasibleregion)最优解(Optimalsolution)该计划的数学模型例2:某工厂拥有A、B、C三种类型的设备,生产甲、乙两种产品。每件产品在生产中需要占用的设备机时数,每件产品可以获得的利润以及三种设备可利用的时数如下表所示:问题:工厂应如何安排生产可获得最大的总利润?解:设变量xi为第i种(甲、乙)产品的生产件数(i=1

第2章 线性规划的图解法.ppt
第2章线性规划的图解法§1线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型线性规划问题的数学模型§2线性规划的图解法§2.1问题的提出§2.1问题的提出例1.目标函数:Maxz=50x
