
拉格朗日乘数法.doc

和蔼****娘子





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

拉格朗日乘数法.doc
应用拉格朗日乘数法,求下列函数的条件极值:(1)若(2)若(其中);(3),若.解(1)设对L求偏导数,并令它们都等于0,则有解之得由于当时,.故函数必在唯一稳定点处取得极小值,极小值(2)设且解方程组得由于当n个正数的积一定时,其和必有最小值,故f一定存在唯一稳定点(c,c,c,c)取得最小值也是极小值,所以极小值f(c,c,c,c)=4c.(3)设,并令解方程组得的六组值为:,,,,.又在有界闭集上连续,故有最值.因此,极小值为极大值为2.(1)求表面积一定而体积最大的长方体;(2)求体积一定而表面积
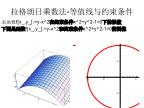
拉格朗日乘数法.ppt
拉格朗日乘数法-等值线与约束条件拉格朗日乘数法-等值线与约束条件拉格朗日乘数法-等值线与约束条件拉格朗日乘数法-等值线与约束条件

拉格朗日乘数法.docx
§4条件极值(一)教学目的:了解拉格朗日乘数法,学会用拉格朗日乘数法求条件极值.(二)教学内容:条件极值;拉格朗日乘数法.基本要求:(1)了解拉格朗日乘数法的证明,掌握用拉格朗日乘数法求条件极值的方法.(2)较高要求:用条件极值的方法证明或构造不等式.(三)教学建议:(1)本节的重点是用拉格朗日乘数法求条件极值.要求学生熟练掌握.(2)多个条件的的条件极值问题,计算量较大,可布置少量习题.(3)在解决很多问题中,用条件极值的方法证明或构造不等式,是个好方法.可推荐给较好学生.在许多极值问题中,函数的自变量

(完整word版)拉格朗日乘数法.doc
应用拉格朗日乘数法,求下列函数的条件极值:(1)若(2)若(其中);(3),若.解(1)设对L求偏导数,并令它们都等于0,则有解之得由于当时,.故函数必在唯一稳定点处取得极小值,极小值(2)设且解方程组得由于当n个正数的积一定时,其和必有最小值,故f一定存在唯一稳定点(c,c,c,c)取得最小值也是极小值,所以极小值f(c,c,c,c)=4c.(3)设,并令解方程组得的六组值为:,,,,.又在有界闭集上连续,故有最值.因此,极小值为极大值为2.(1)求表面积一定而体积最大的长方体;(2)求体积一定而表面积

(完整word版)拉格朗日乘数法.doc
应用拉格朗日乘数法,求下列函数的条件极值:(1)若(2)若(其中);(3),若.解(1)设对L求偏导数,并令它们都等于0,则有解之得由于当时,.故函数必在唯一稳定点处取得极小值,极小值(2)设且解方程组得由于当n个正数的积一定时,其和必有最小值,故f一定存在唯一稳定点(c,c,c,c)取得最小值也是极小值,所以极小值f(c,c,c,c)=4c.(3)设,并令解方程组得的六组值为:,,,,.又在有界闭集上连续,故有最值.因此,极小值为极大值为2.(1)求表面积一定而体积最大的长方体;(2)求体积一定而表面积
