2.1变化的快慢与变化率微课获奖课件公开课一等奖课件省赛课获奖课件.pptx

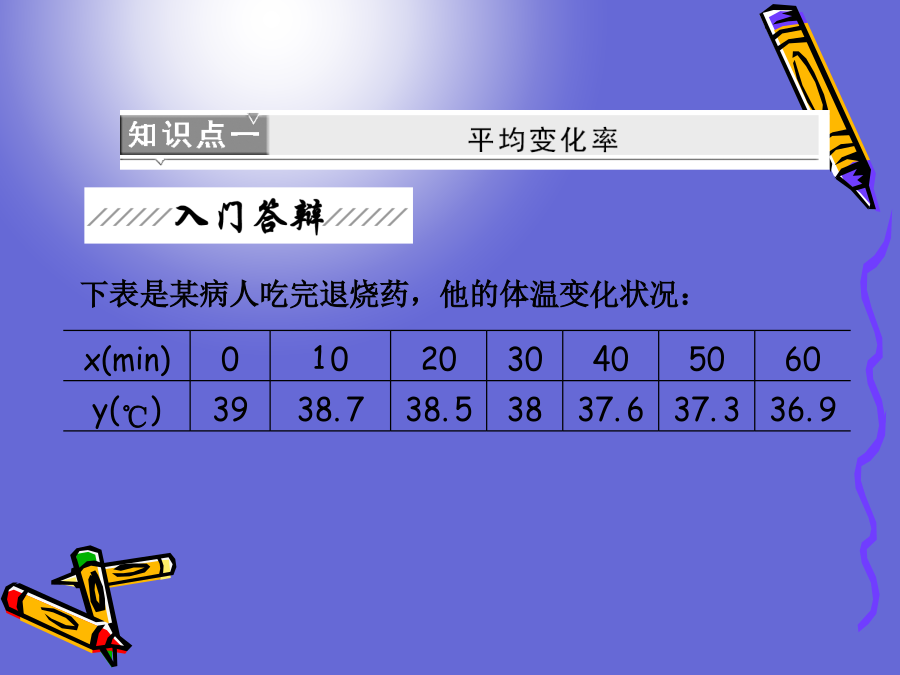
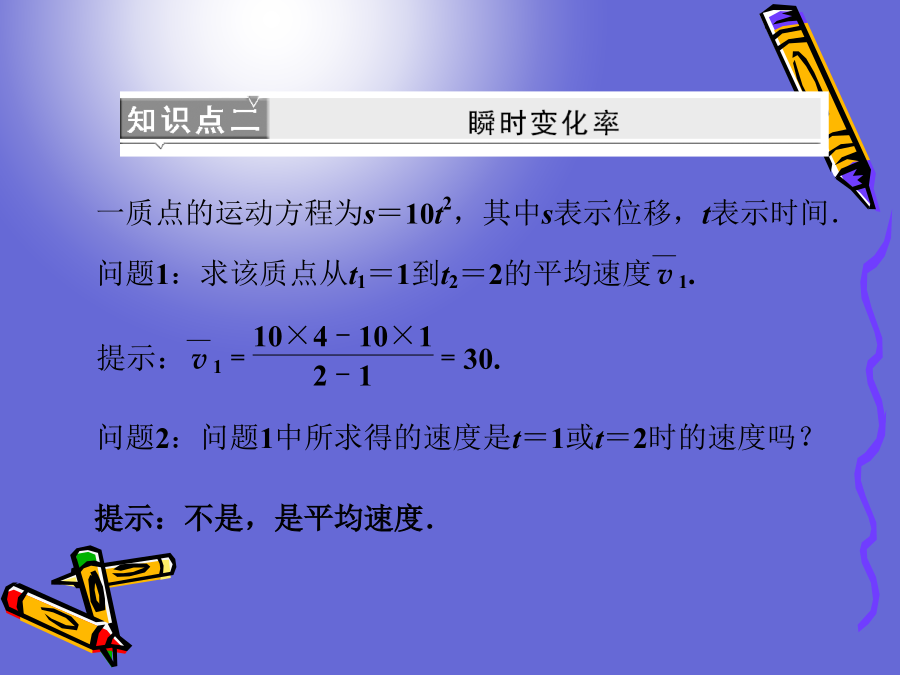
第二章下表是某病人吃完退烧药，他的体温变化状况：问题1：观察上表，每10分钟病人体温变化相似吗？提示：不相似．问题2：哪段时间体温变化较快？提示：从20min到30min变化快．问题3：如何刻画体温变化的快慢？提示：用单位时间内的温度变化的大小，即体温的平均变化率．x2－x1提示：不是，是平均速度．Δx趋于0(1)函数的平均变化率可正可负，反映函数y＝f(x)在[x1，x2]上变化的快慢，变化快慢是由平均变化率的绝对值决定的，且绝对值越大，函数值变化得越快．(2)平均速度和瞬时速度都是反映运动物体的位移随时间变化而变化的状况．平均速度是运动物体在一种时间段里位移的变化量与这段时间的比值，而瞬时速度是运动物体在某一时刻的速度，当一种时间段趋于0时的平均速度就是瞬时速度．[例1]已知函数f(x)＝2x2＋1.(1)求函数f(x)在[2,2.01]上的平均变化率；(2)求函数f(x)在[x0，x0＋Δx]上的平均变化率．[思路点拨]先求Δx，Δy，再运用平均变化率的定义求解．1．已知函数y＝f(x)＝x2＋1，则在x1＝2，x2＝2.1时，Δy的值为()A．0.40B．0.41C．0.43D．0.44解析：Δy＝f(2.1)－f(2)＝0.41.答案：B2．已知函数f(x)＝x2，分别计算函数f(x)在区间[1,3]，[1,2]，[1,1.1]，[1,1.001]上的平均变化率．[例2]已知s(t)＝5t2.(1)求t从3秒到3.1秒的平均速度；(2)求t从3秒到3.01秒的平均速度；(3)求t＝3秒时的瞬时速度．[一点通]在某一时间段内的平均速度与时间段Δt有关，随Δt变化而变化；但求某一时刻的瞬时速度时，Δt是趋于0，而不是Δt＝0，此处Δt是时间间隔，可任意小，但绝不能认为是0.3．一种运动物体以某建筑物为参考物，有关时间t的位移函数为s(t)＝t2－4t＋5，求：(1)t∈[1,1.5]的平均速度及t＝1时的瞬时速度；(2)t∈[2.5,3]的平均速度及t＝3时的瞬时速度．4．一辆汽车按规律s＝at2＋1做直线运动，若汽车在t＝2时的瞬时速度为12，求a.(1)瞬时变化率的绝对值度量函数在某点处变化的快慢．(2)当瞬时变化率不不大于0时，阐明函数值在增加；当瞬时变化率不大于0时，阐明函数值在减小；其绝对值大小才干阐明变化的快慢．(3)平均变化率是曲线陡峭程度的“数量化”，曲线陡峭程度是平均变化率的“视觉化”．点击此图片进入“应用创新演习”