测控说课稿公开课一等奖课件省赛课获奖课件.pptx

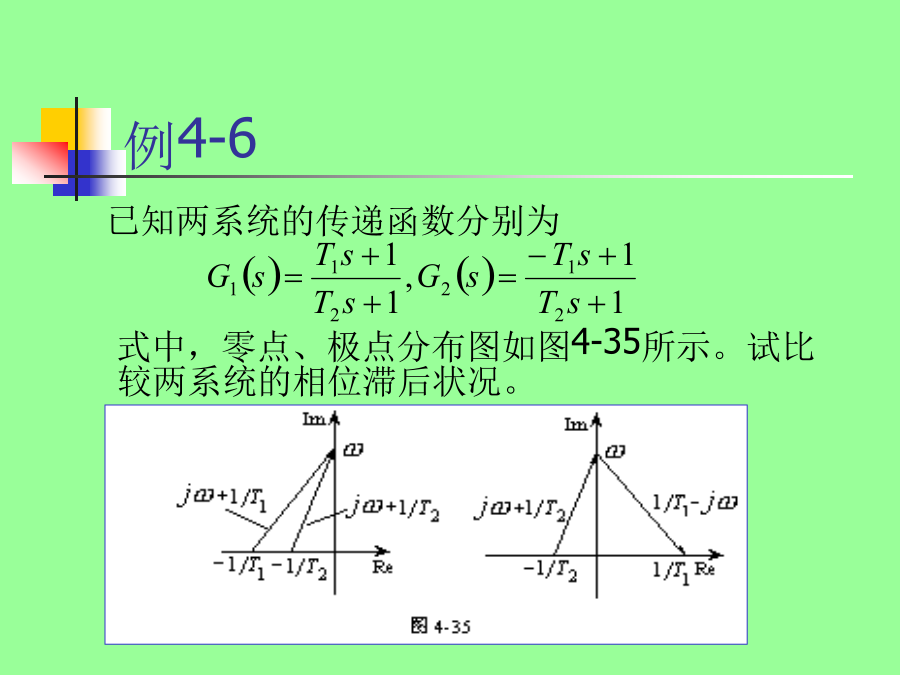
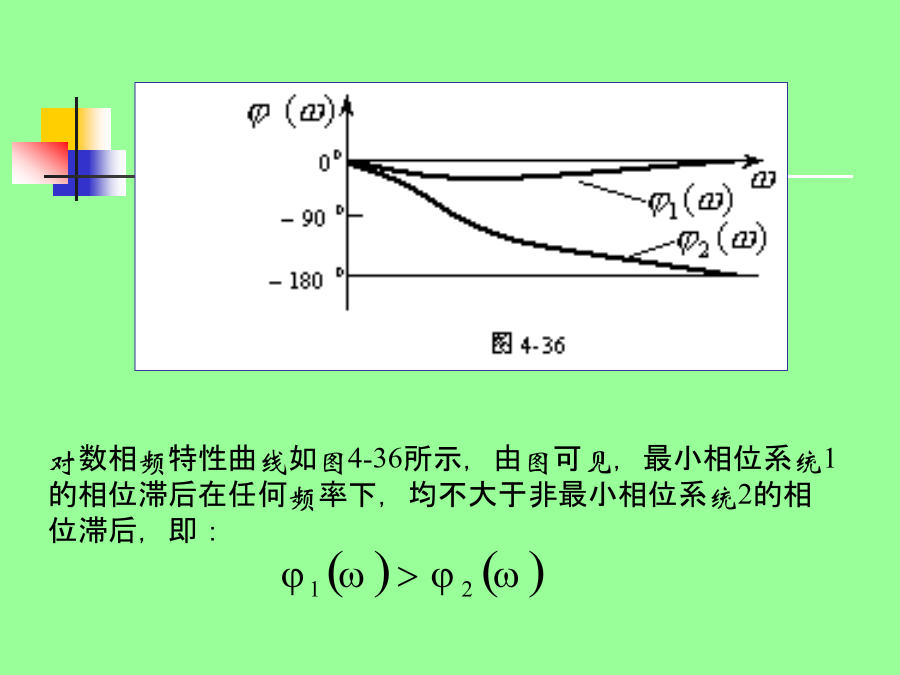
§4-4最小和非最小相位系统在稳定的系统中，如果幅频特性相似，对于任意给定频率，最小相位系统的相位滞后是最小的。例4-6解由最小相位系统定义知，系统1为最小相位系统，系统2为非最小相位系统。两系统的频率特性分别为：显然，两系统的对数幅频特性相似，即：两系统的对数相频特性分别为：对数相频特性曲线如图4-36所示，由图可见，最小相位系统1的相位滞后在任何频率下，均不大于非最小相位系统2的相位滞后，即：例4-7解：系统1为最小相位系统。系统2是非最小相位系统。两系统的频率特性分别为：显然，两系统的对数幅频特性相似，即：而对数相频特性分别为：对数频率特性如图4-37所示。由图（b）可见，最小相位系统1相位滞后小。二、对数幅频特性和对数相频特性的关系例4-8解：由图4-38可直接写出系统的传递函数为：由图查得：因此K=0.2于是得系统的传递函数为：对于最小相位系统，当时，其相位为-90°（n-m），其对数幅频特性曲线的斜率为-20（n-m）dB/dec，其中m、n分别为传递函数分子分母多项式的最高阶次（n>m），而对于非最小相位系统，当时，相位不等于-90°（n-m）。