含圆孔和裂纹板应力强度因子分析.pdf

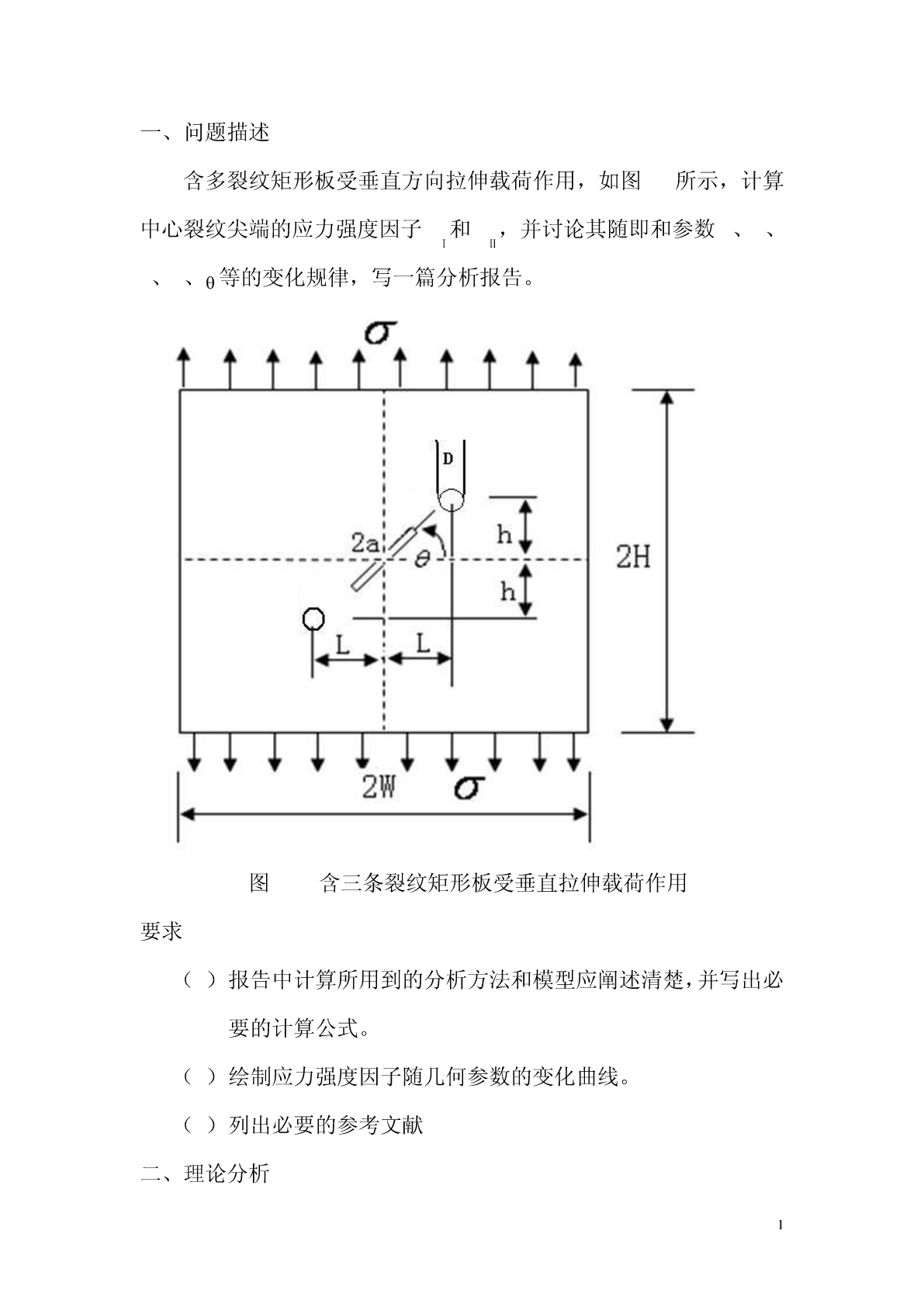
《断裂力学》大作业题目：含圆孔和裂纹板应力强度因子分析姓名：学号：专业：授课教师：一、问题描述含多裂纹矩形板受垂直方向拉伸载荷作用，如图1所示，计算中心裂纹尖端的应力强度因子K和K，并讨论其随即和参数L、h、ⅠⅡa、D、等的变化规律，写一篇分析报告。图1.含三条裂纹矩形板受垂直拉伸载荷作用要求（1）报告中计算所用到的分析方法和模型应阐述清楚，并写出必要的计算公式。（2）绘制应力强度因子随几何参数的变化曲线。（3）列出必要的参考文献二、理论分析1在线弹性断裂力学中，I型裂纹尖端的应力场为：K3Icos(1sinsin)x2222rK3Icos(1sinsin)y2r222K3Isincoscosxy2r222I型裂纹尖端的位移场为：(1)Kr3uI[(21)cos(1cos)2E222(1)Kr3vI[(21)sinsin2E22234平面应变其中：3平面应力1同理，对II型裂纹尖端的应力场：K3IIsin(2coscos)x2222rK3IIcossincosy2r222K3IIcos(1sinsin)xy2r222显然，位移场和应力场均可以表示成应力强度因子的形式。通过对裂纹尖端的应力应变场分析来求解对应的应力强度因子，便是传统有限元求解应力强度因子的原理。而对于I、II复合型裂纹尖端的应力强度因子，可通过它们的叠加获得。确定应力强度因子的方法有3大类：解析法、数值解法和实验方法。解析法只能计算简单问题，大多数问题需要采用数值解法，当前工程中广泛采用的数值解法是有限单元法。随着有限元法的发展，有限元在断裂力学中的应用越来越普及。近年来，计算机技术得到了迅猛发2展，许多功能强大的有限元软件也相继问世，大型通用有限元程序abaqus就是当前工程中应用最广泛的有限元软件之一。采用abaqus软件计算裂纹尖端的应力强度因子，通过阅读abaqus的帮助文件，得到abaqus基于有限元方法在线弹性范围内计算应力强度因子的原理。三、具体分析方法、模型和载荷的确定从裂纹尖端邻域的应力场分布可以看出，裂纹尖端的应力场具有奇异性，靠近裂纹尖端的各应力分量都与r成正比，当r一0时，应力急剧增长。在常规的有限元法中，用多项式表示单元内部应力和位移，在奇异点附近不能很好地反映应力的变化。为了克服这个困难，在裂纹尖端附近设置特殊的奇异单元。以反映应力场在裂纹附近的奇异性。奇异单元是由正常的二次等参单元修改而成，在邻近尖端的边上，把节点放在离裂尖的1／4处，奇异单元法能精确地计算出应力强度因子。有限元中计算应力强度因子的方法有位移相关技术、应力相关技术等，比较常用的是位移相关技术。Abaqus使用的是位移插值技术，和位移相关技术一样也是利用裂纹尖端单元节点的位移来求应力强度因子。为了保证计算精度可以使用自适应方法求解，裂纹周向单元越多，单元边长越小，计算结果越精确。选用的材料板，宽2W=120mm，高2H=100mm,厚度为b=5mm，杨氏模量E=2.2E5N/mm2，泊松比μ=0.25。整体单元类型选用八节点四变形等参单元，在裂纹尖端用正常的二次等参单元修改而成的奇异单3元，把节点放在离裂尖的1／4处。矩形板两端垂直于裂纹线的方向施加一拉应力σ=100Mp。在有限元中网格划分如图1：图1：网格划分图应变及应力图如图2，图34图2：mises应力图5图3：变形模量图四、具体分析参数L、h、a、D、对裂纹尖端的应力强度因子的影响本计算数据是通过改变命令流中各关键点的坐标，从而实现各参数的相应改变而得到的。在计算中取弹性模量E=220Gpa,泊松比μ=0.25，拉应力σ=100Mpa.1.L为单变量对应力强度因子KI、KII的影响(1)取取h=20,a=10,=30°，D=10,L为变量，记录应力强度因子KI、KII。6①取L=25KI=333.4KII=201.3②取L=30KI=321.16KII=204.4③取L=35KI=318.4KII=205.3（2）绘制曲线（3）分析参数L对裂纹尖端的应力强度因子KI的影响。从L对KI、KII的影响曲线我们可以看出,应力强度因子KI、KII均随着L的增大而减少，但变化不是很大。当L/W≧0.6时，L的变化对应力强度因子几乎就没有了影响。2.为单变量对应力强度因子hKI、KII的影响（1）取L=30,a=10,=30°，D=10,h为变量，记录应力强度因子KI、KII。①取h=10KI=331.2KII=206.2②取h=20KI=321.16KII=204.47③取h=30KI=315.3KII=200.5（2）绘