太原理工大学数值计算方法实验报告.pdf

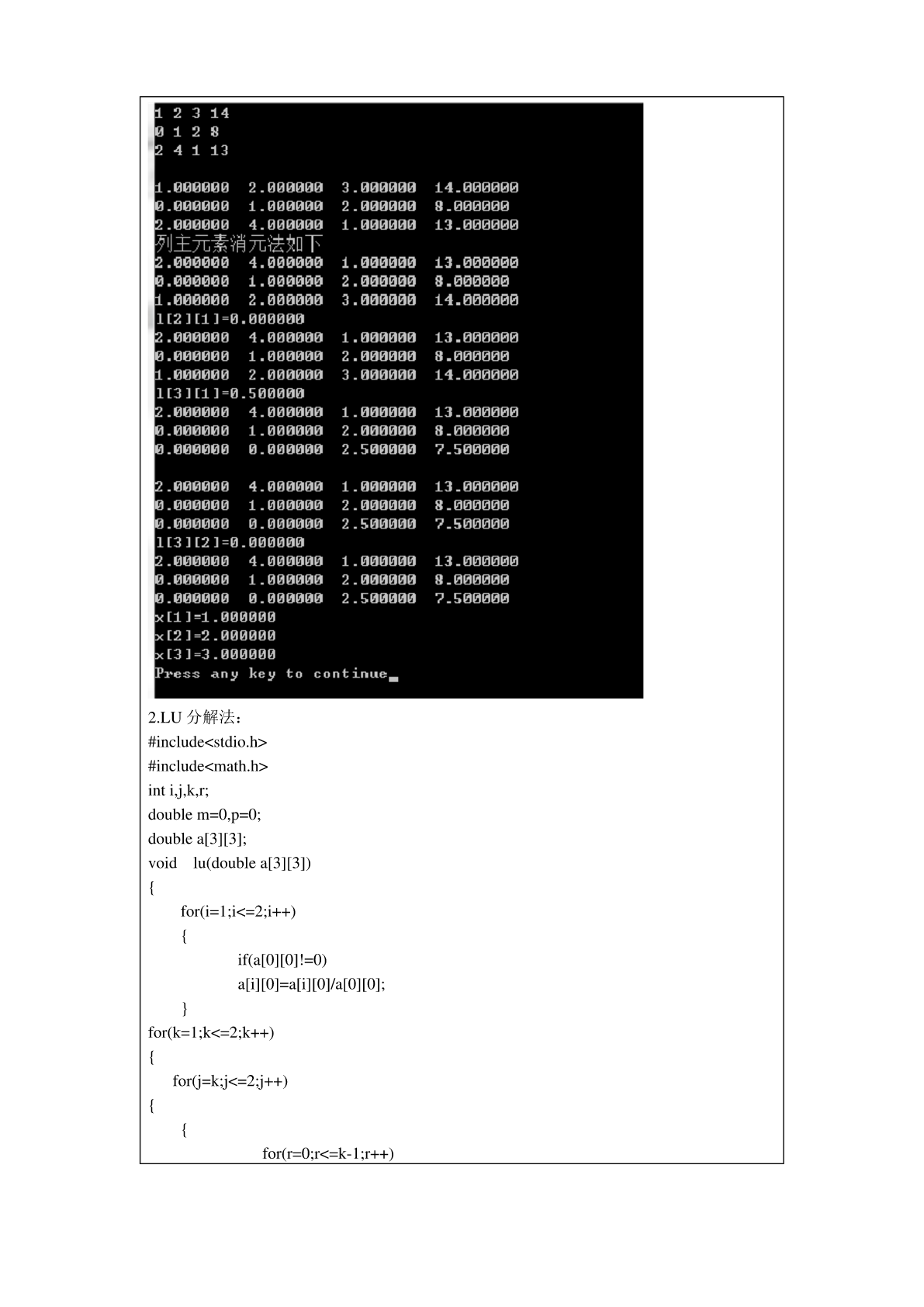
本科实验报告课程名称：计算机数值方法实验项目：方程求根、线性方程组的直接解法、线性方程组的迭代解法、代数插值和最小二乘拟合多项式实验地点：行勉楼专业班级：********学号：*********学生姓名：********指导教师：李誌，崔冬华2016年4月8日学生姓名实验成绩实验名称实验一方程求根实验内容和要求熟悉使用二分法、迭代法、牛顿法、割线法等方法对给定的方程进行根的求解。选择上述方法中的两种方法求方程：f(x)=x3+4x2-10=0在[1,2]内的一个实根，且要求满足精度|x*-x|<0.5×10-5n（1）了解非线性方程求根的常见方法，如二分法、牛顿法、割线法。（2）加深对方程求根方法的认识，掌握算法。（3）会进行误差分析，并能对不同方法进行比较。实验原理1.二分法：如果要求已知函数f(x)=0的根(x的解)，那先要找出一个区间[a,b]，使得f(a)与f(b)异号。根据介值定理，这个区间内一定包含着方程式的根。求该区间的中点m=(a+b)/2，并找出f(m)的值。若f(m)与f(a)正负号相同，则取[m,b]为新的区间,否则取[a,m]。重复第3步和第4步，直到得到理想的精确度为止。2.割线法是利用牛顿迭代法的思想,在根的某个领域内，函数有直至二阶的连续导数，并且不等于0，则在领域内选取初值x,x,迭代均收敛。01（1）在区间[m,n]内输入初值x0，x1.（2）计算x2。x2=x1-f(x1)*(x1-x0)/(f(x1)-f(x0))（3）x0=x1,x1=x2（4）判断是否达到精度,若是输出x1，若否执行（2）主要仪器设备HP计算机实验记录1.二分法//方程求根（二分法）.cpp:定义控制台应用程序的入口点。//#include"stdafx.h"#include"iostream"usingnamespacestd;classText{public:floatx,y,a,b,c,n=0;voidGetab(){cout<<"请输入计算区间：(以空格隔开)"<<endl;cin>>a>>b;}floatGetY(floatx){y=x*x*x+4*x*x-10;returny;}floatCalculate(floata,floatb){c=(a+b)/2;n++;if(GetY(c)==0||((b-a)/2)<0.000005){cout<<c<<"为方程的解"<<endl;return0;}if(GetY(a)*GetY(c)<0){returnCalculate(a,c);}if(GetY(c)*GetY(b)<0){returnCalculate(c,b);}}};intmain(){cout<<"方程组为：f(x)=x^3+4x^2-10=0"<<endl;floata,b;Texttext;text.Getab();a=text.a;b=text.b;text.Calculate(a,b);return0;}2.割线法：//方程求根（割线法）.cpp:定义控制台应用程序的入口点。//#include"stdafx.h"#include"iostream"usingnamespacestd;classA{public:floatx0,x1,y;floatGetY(floatx){y=x*x*x+4*x*x-10;returny;}voidGetNumber(){cout<<"请输入两个初始近似值：(以空格隔开)"<<endl;cin>>x0;cin>>x1;}voidCalculate(floatx0,floatx1){floatx2;x2=x1-(GetY(x1)/(GetY(x1)-GetY(x0))*(x1-x0));if(x2==x1){cout<<x2<<"为方程的解"<<endl;}else{cout<<x2<<endl;returnCalculate(x1,x2);}}};intmain(){cout<<"方程组为：f(x)=x^3+4x^2-10=0"<<endl;floata,b;Atext;text.GetNumber();a=text.x0;b=text.x1;text.Calculate(a,b);return0;}心得体会使用不同的方法，可以不同程度的求得方程的解，通过二分法计算的程序实现更加了解二分法的特点，二分法过程简单，程序容易实现，但该方法收敛比较慢一般用于求根的初始近似值，不同的方法速度不同。面对一个复杂的问题，要学会简化处理步骤，分步骤一点一点的循序处理，只有这样，才能高效的解决一个复杂问题。实验名称实验二线性方程组的直接求解实验内容和要求合理选择利用Gauss消元法、主元素消元法、LU分解法、追赶法求解下列方程组：123x141012x