动态规划的建模与求解.pptx

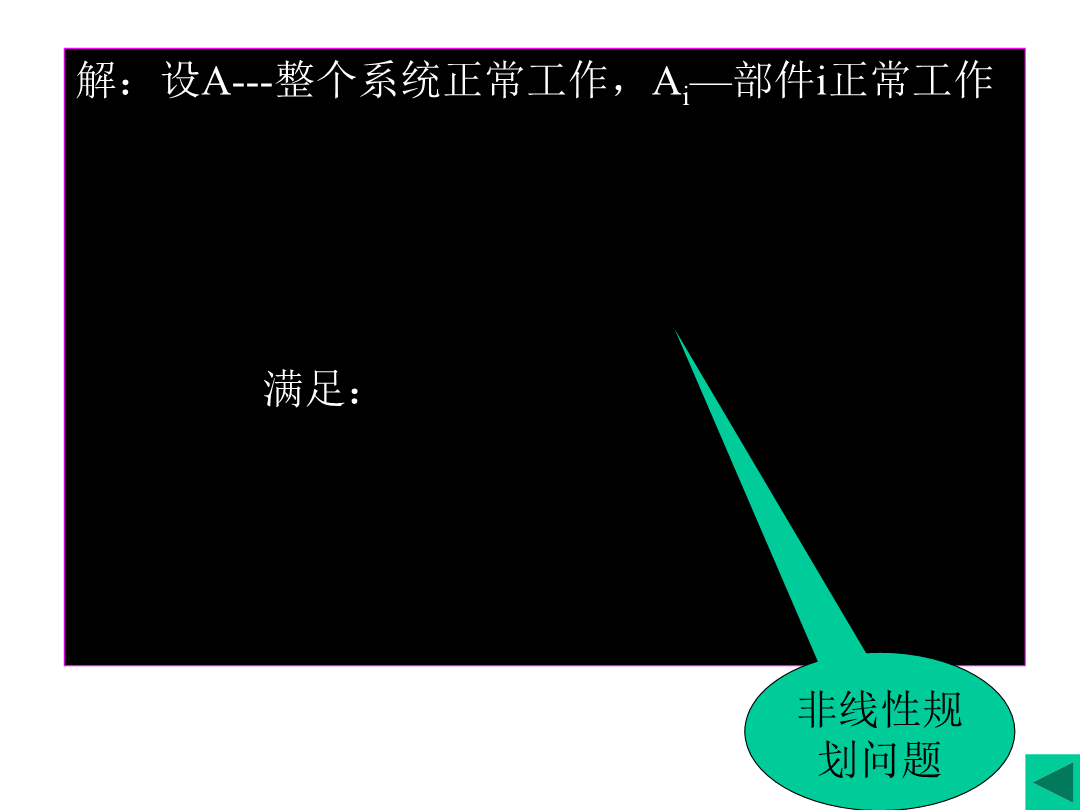
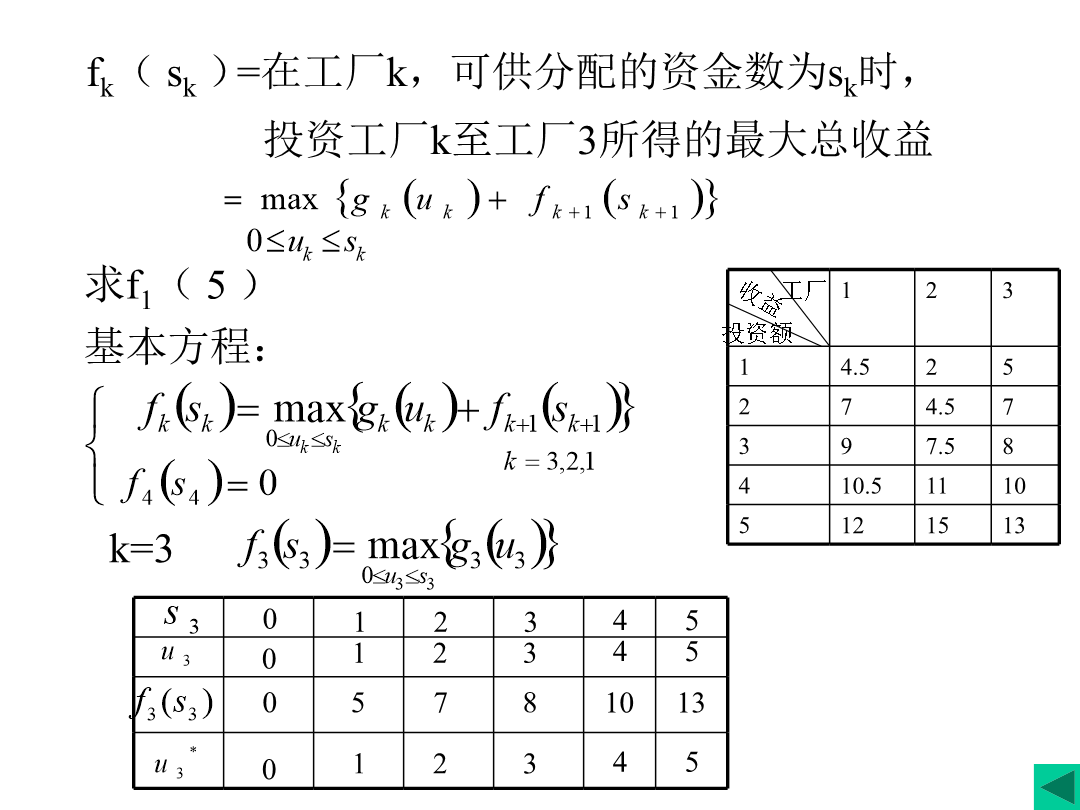
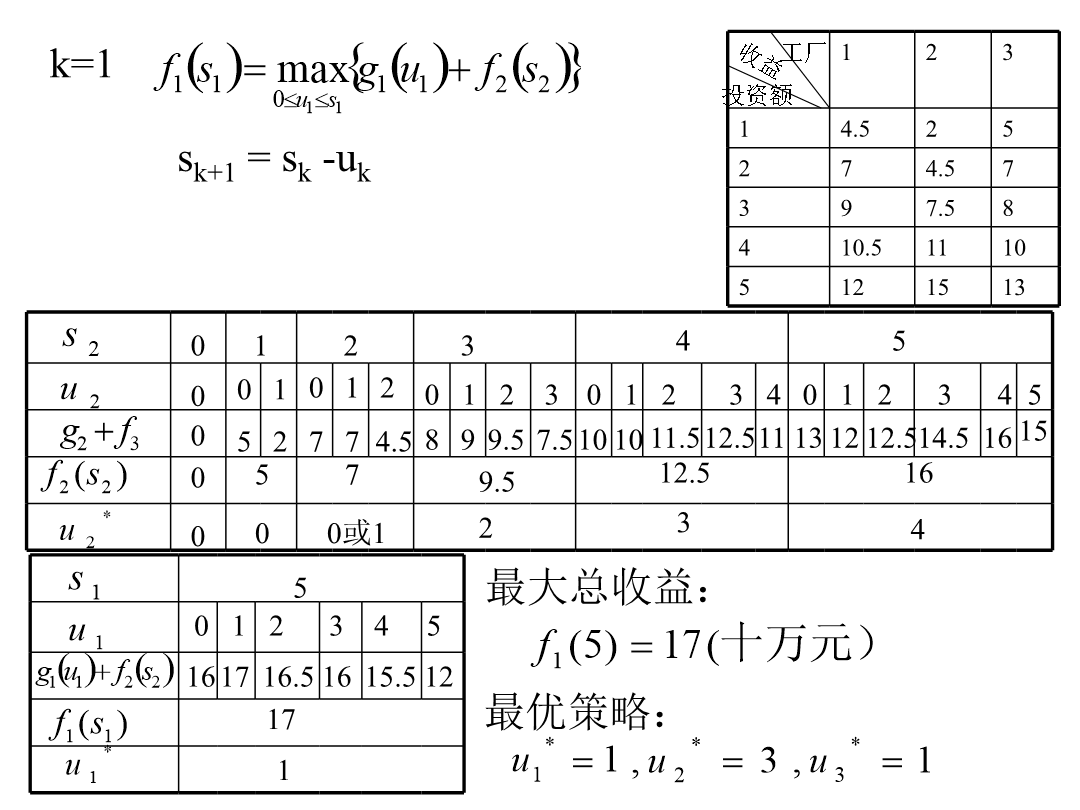
4.3动态规划的建模与求解4.3.1建摸2、动态规划模型的几个要素：3)具有明确的指标函数，且阶段指标值可以计算边界条件：解：设A---整个系统正常工作，Ai—部件i正常工作最优指标函数fk(sk，yk）=4.4.2动态规划模型的求解fk（sk）k=1例（季节工问题）某工厂的生产任务随季节波动，为降低成本宜用季节临时工，但熟练的生产工人临时难以聘到，培训新手费用又高，各季节工人需用量如下表所示，每季节超过需用量聘用，每人浪费2000元，聘用或解聘费为200元乘上两个季节聘用人数之差的平方，问厂长一年中应如何聘用工人可使总花费最小？（假定工资按实际工作时间计算，则聘用人数可为分数）基本方程：min{}min{}3、建立动态规划模型的基本要求：例（资源分配问题）系统由n个部件串联组成，每一个部件上装有备用件，部件i(i=1,2,…,n)上装有xi个备用元件时，正常工作的概率为pi（xi）。设装一个i部件的设备元件费用为ci，重量wi为，要求总费用不超过C，总重量不超过W，问如何选择个部件的备用元件数，使整个系统的工作可靠性最大？动态规划基本方程：投资额k=2二、连续变量的解法解：f3（s3）f2（s2）f4（s4）=