卡尔曼滤波两例题含matlab程序汇总.pdf

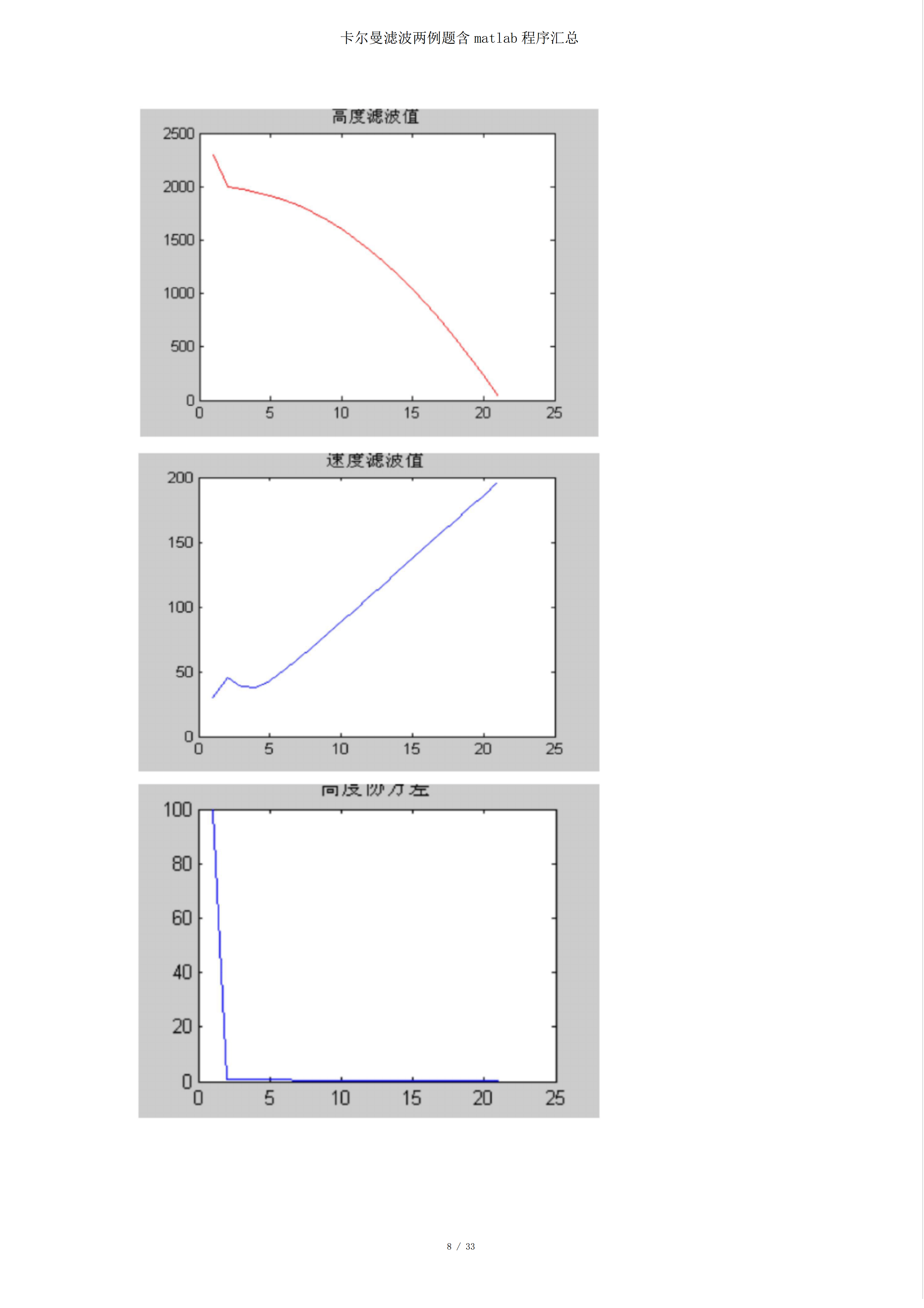
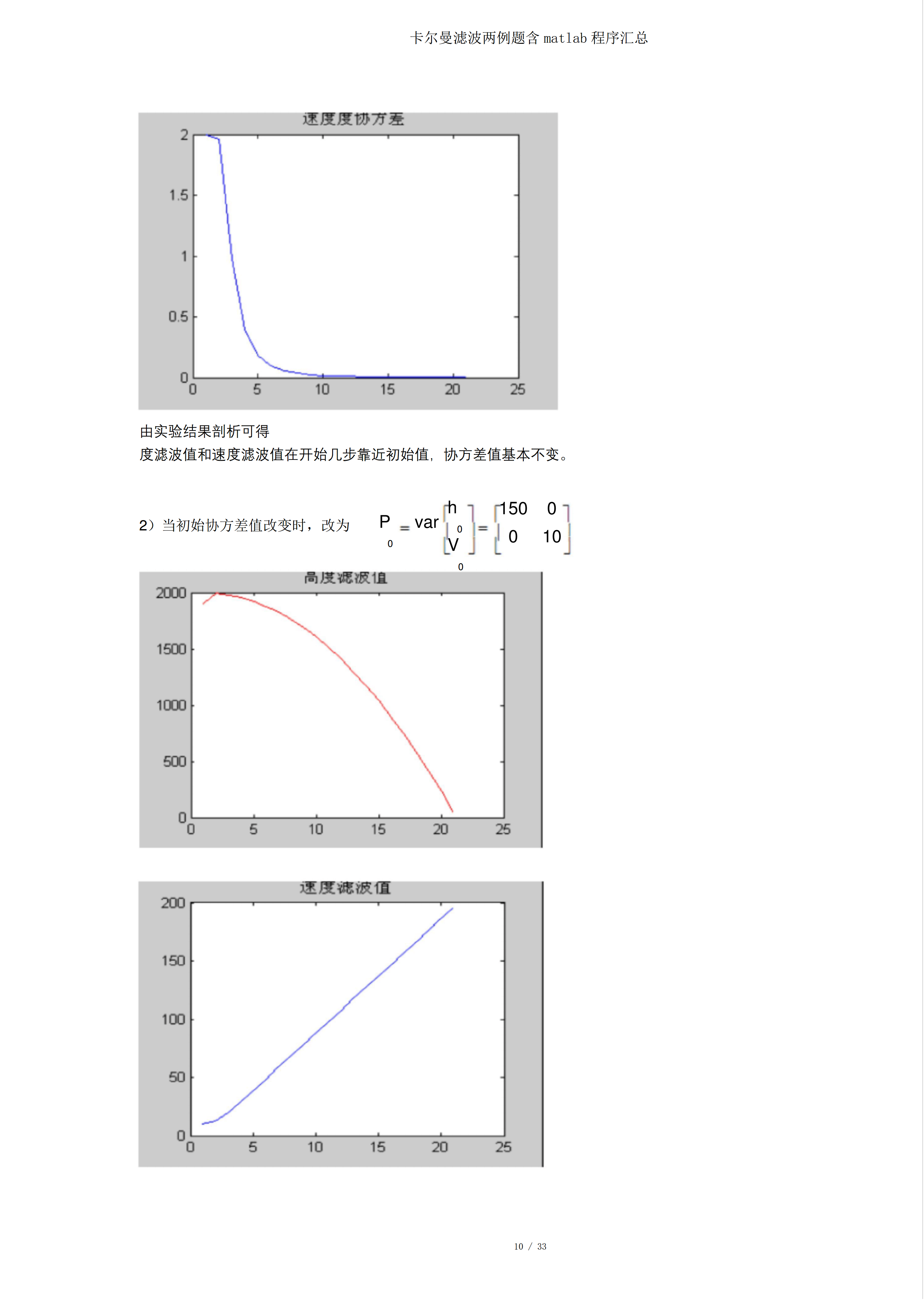
卡尔曼滤波两例题含matlab程序汇总一.已知一物体作自由落体运动，对其高度进行了20次丈量，丈量值以下表：时间[s]1234567高度[km]1.99451.97941.95541.92141.87771.82501.7598时间[s]891011121314高度[km]1.68671.60361.50921.40761.29441.17241.0399时间[s]151617181920高度[km]0.89800.74550.58500.41250.23180.0399设高度的丈量偏差是均值为0、方差为1的高斯白噪声随机序列，该物体的初始高度hV和速度00Ehmh也是高斯散布的随机变量，且19001000。试求该物体高度0,Pvar00EV10m/sV0200和速度随时间变化的最优预计。（2g9.80m/s）解：h(k)1.令t=1R（k）=1Q(k)=0X(k)v(k)依据失散时间卡尔曼滤波公式，则有：X(k1)(k1,k)X(k)U(k)Y(k1)H(k1)X(k1)V(k1)1t0.5gt2U(k)＝1gt(k1,k)H(k1)10＝＝1900^滤波初值：X(0|0)EX(0)10100P(0|0)var[X(0)]P02^^一步展望：X(k1|k)(k1,k)X(k|k)U(k)TP(k1|k)(k1,k)P(k|k)(k1,k)TT1滤波增益：K(k1)P(k1|k)H(k1)[H(k1)P(k1|k)H(k1)R(k1)]^^^滤波计算：X(k1|k1)X(k1|k)K(k1)[Y(k1)H(k1)X(k1|k)]1/33卡尔曼滤波两例题含matlab程序汇总P(k1|k1)[IK(k1)H(k1)]P(k1|k)2.实验结果2/33卡尔曼滤波两例题含matlab程序汇总3/33卡尔曼滤波两例题含matlab程序汇总高度随时间变化预计速度随时间变化的最优预计高度协方差4/33卡尔曼滤波两例题含matlab程序汇总5/33卡尔曼滤波两例题含matlab程序汇总速度协方差从以上的结果，能够获得高度和速度的预计值，再经过所获得的高度协方差和速度协方差，可见用卡尔曼滤波法，固然刚开始的初始高度协方差很大为100，但经过2步以后减小到不超出1，渐渐靠近于0，相同的速度协方差刚开始的时候也比较大，为2，可是经过5步以后快速减小，到10步以后靠近于0。3.相关参数的影响（比如初始条件、噪声统计特征对滤波结果的影响等）；Eh2300m1）初始条件改变时，改变初始高度值，和速度值0EV30m/s06/33卡尔曼滤波两例题含matlab程序汇总7/33卡尔曼滤波两例题含matlab程序汇总8/33卡尔曼滤波两例题含matlab程序汇总9/33卡尔曼滤波两例题含matlab程序汇总由实验结果剖析可得度滤波值和速度滤波值在开始几步靠近初始值，协方差值基本不变。h15002）当初始协方差值改变时，改为Pvar00100V010/33卡尔曼滤波两例题含matlab程序汇总11/33卡尔曼滤波两例题含matlab程序汇总实验结果剖析高度和速度滤波值基本不变，速度协方差和高度协方差开始要靠近速度协方差和高度协方差的初始值。可是经过几步以后，都趋于0。二．相同考虑自由落体运动的物体，用雷达（和物体落地址在同一水平面）进行丈量，如图所Ed1995md50000示。假如Eh2005m,Pvarh050，且雷达测距和测角的丈量噪声000EV1m/sV002000.40是高斯白噪声随机序列，均值为零、方差阵R，试依据以下丈量数据确立00.01物体的高度和速度随时间变化的预计值。时间[s]*1000斜距[km]俯仰角[rad]*10000.000500000000002.827416437818910.000758504358760.000832822604782.820666869662360.0006780824163912/33卡尔曼滤波两例题含matlab程序汇总13/33卡尔曼滤波两例题含matlab程序汇总0.002000000000000.000852790368020.002500000000002.806717865362440.000729007684520.003000000000002.797252689740890.000800724818190.003500000000002.786642734750390.000750955762130.004000000000002.773203650263130.000657627253790.004500000000000.000811861485450.005000000000002.743312886281950.000797837270340.005500000000002.725