直接证明与间接证明(1)-豆柴文库

直接证明与间接证明(1).ppt

2024-02-23

11金币

226KB

8页

胜利****实阿

实名认证

内容提供者

1/8

2/8

3/8

4/8

5/8

6/8

7/8

8/8

在线预览结束，喜欢就下载吧，查找使用更方便

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

直接证明与间接证明(1).ppt

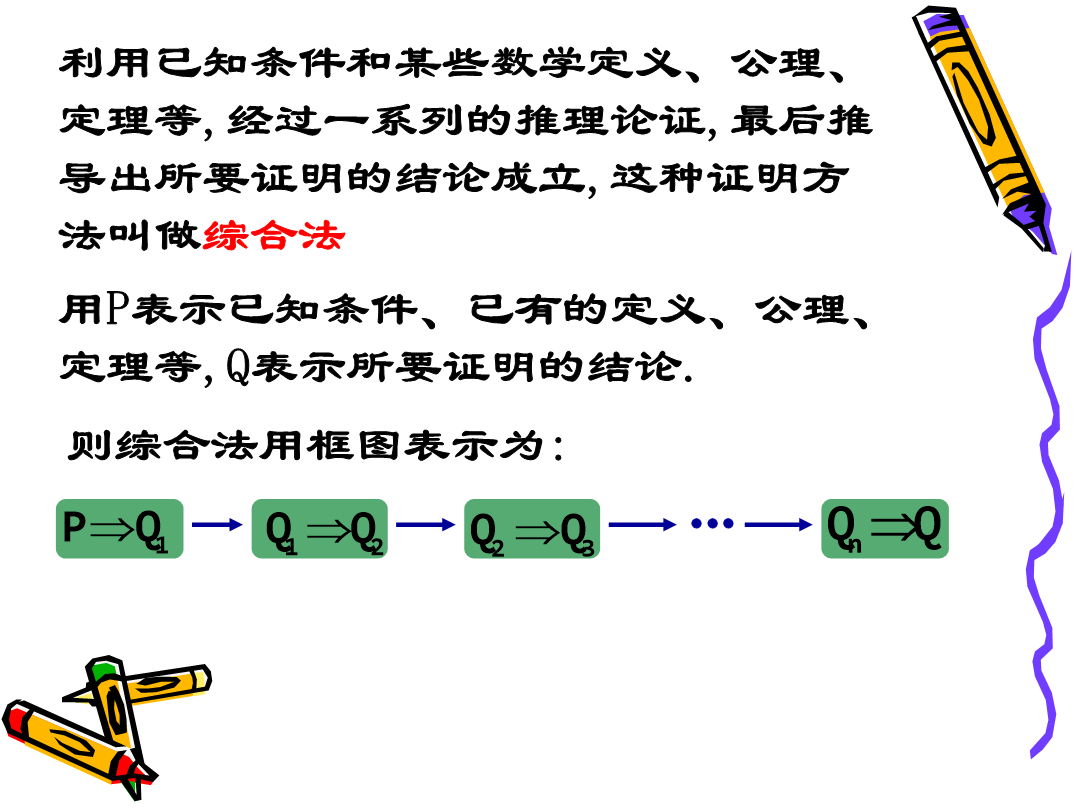
2.2直接证明与间接证明演绎推理是证明数学结论、建立数学体系的重要思维过程.例:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法例：在△ＡＢＣ中，三个内角Ａ、Ｂ、Ｃ对应的边分别为a、b、c，且Ａ、Ｂ、Ｃ成等差数列，a、b、c成等比数列，求证△ＡＢＣ为等边三角形．例：设抛物线y2=2px(p>0)的焦点为Ｆ，经过点Ｆ的直线交抛物线于Ａ、Ｂ两点，点Ｃ在抛物线的准线上，且ＢＣ∥

直接证明与间接证明-1.doc

§2.2直接证明与间接证明(1)知识框架证明直接证明间接证明数学归纳法综合法分析法反证法直接证明综合法分析法定义从已知条件出发，以已知的定义、公理、定理为依据，逐步下推，直到推出要证明的结论为止.从问题的结论出发，追溯导致结论成立的条件，逐步上溯，直到使结论成立的条件和已知事实吻合为止.思维过程由因导果执果索因证题步骤P(已知)⇒P1⇒P2⇒…⇒Pn⇒Q(结论)Q(结论)⇐Q1⇐Q2⇐…⇐Qn⇐P(已知)文字语言因为…，所以…或由…，得…要证…，只需证…，即证…符号语言⇒⇐判

直接证明与间接证明（1）.ppt

2.2直接证明与间接证明演绎推理是证明数学结论、建立数学体系的重要思维过程.例:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法例：在△ＡＢＣ中，三个内角Ａ、Ｂ、Ｃ对应的边分别为a、b、c，且Ａ、Ｂ、Ｃ成等差数列，a、b、c成等比数列，求证△ＡＢＣ为等边三角形．例：设抛物线y2=2px(p>0)的焦点为Ｆ，经过点Ｆ的直线交抛物线于Ａ、Ｂ两点，点Ｃ在抛物线的准线上，且ＢＣ∥

直接证明与间接证明-1.doc

§2.2直接证明与间接证明(1)知识框架证明直接证明间接证明数学归纳法综合法分析法反证法直接证明综合法分析法定义从已知条件出发，以已知的定义、公理、定理为依据，逐步下推，直到推出要证明的结论为止.从问题的结论出发，追溯导致结论成立的条件，逐步上溯，直到使结论成立的条件和已知事实吻合为止.思维过程由因导果执果索因证题步骤P(已知)⇒P1⇒P2⇒…⇒Pn⇒Q(结论)Q(结论)⇐Q1⇐Q2⇐…⇐Qn⇐P(已知)文字语言因为…，所以…或由…，得…要证…，只需证…，即证…符号语言⇒⇐判断下面结论是否正确(请在括号中

直接证明与间接证明(1).ppt

2.2直接证明与间接证明演绎推理是证明数学结论、建立数学体系的重要思维过程.例:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法例：在△ＡＢＣ中，三个内角Ａ、Ｂ、Ｃ对应的边分别为a、b、c，且Ａ、Ｂ、Ｃ成等差数列，a、b、c成等比数列，求证△ＡＢＣ为等边三角形．例：设抛物线y2=2px(p>0)的焦点为Ｆ，经过点Ｆ的直线交抛物线于Ａ、Ｂ两点，点Ｃ在抛物线的准线上，且ＢＣ∥

收藏立即下载