课件-全国-2019_（潍坊专版）2019中考数学复习 第1部分 第三章 函数 第二节 一次函数的图象与性质课件.ppt

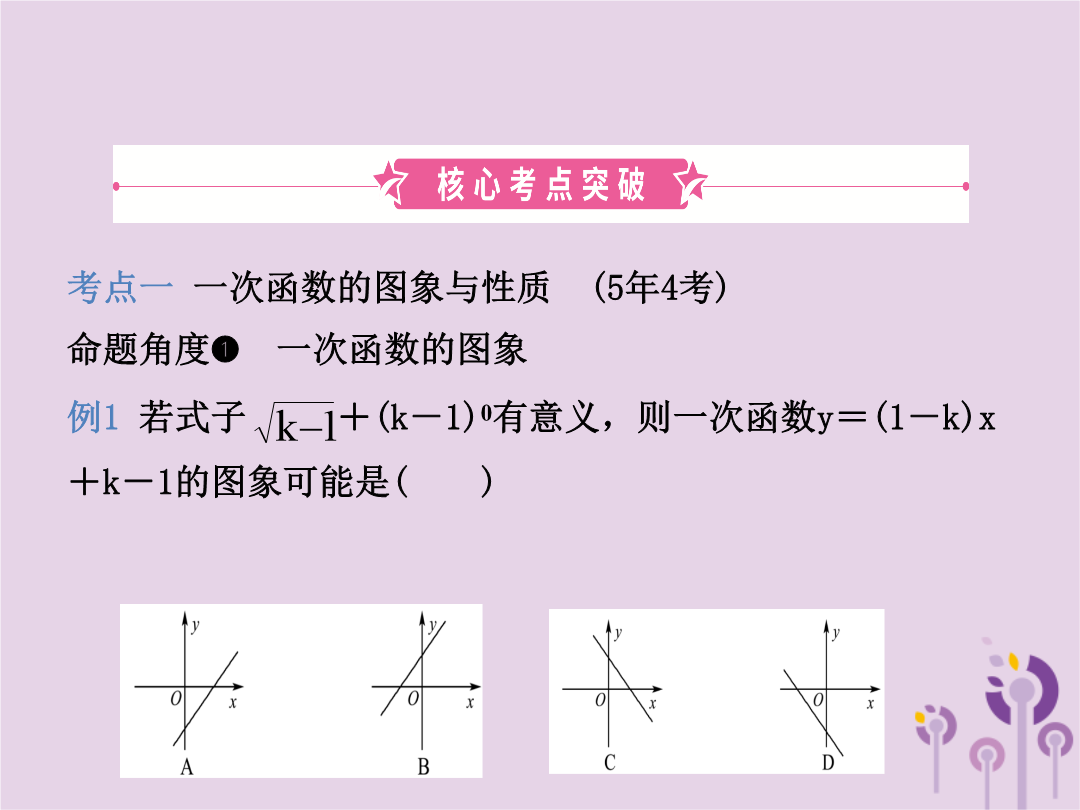
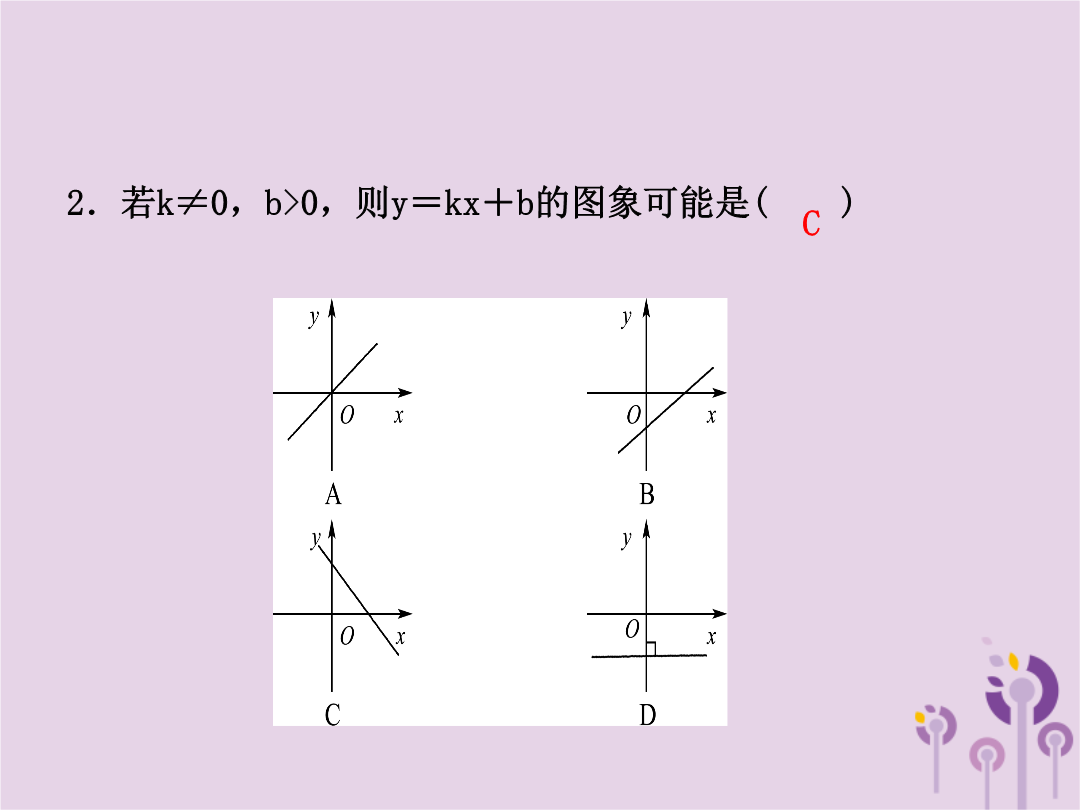
第二节一次函数的图象与性质考点一一次函数的图象与性质(5年4考)命题角度❶一次函数的图象例1若式子＋(k－1)0有意义，则一次函数y＝(1－k)x＋k－1的图象可能是()【分析】先求出k的取值范围，再判断出1－k及k－1的符号，进而可得出结论．【自主解答】∵式子＋(k－1)0有意义，∴解得k＞1，∴1－k＜0，k－1＞0，∴一次函数y＝(1－k)x＋k－1的图象过一、二、四象限．故选C.1．(2018·寿光模拟)若实数a，b，c满足a＋b＋c＝0，且a<b<c，则函数y＝cx＋a的图象可能是()2．若k≠0，b>0，则y＝kx＋b的图象可能是()命题角度❷一次函数的性质例2直线y＝－x＋1经过的象限是()A．第一、二、三象限B．第一、二、四象限C．第二、三、四象限D．第一、三、四象限【分析】根据一次函数的性质解答即可．【自主解答】由于k＝－1＜0，b＝1＞0，故函数过第一、二、四象限．故选B.3．(2018·常德中考)若一次函数y＝(k－2)x＋1的函数值y随x的增大而增大，则()A．k＜2B．k＞2C．k＞0D．k＜04．(2017·呼和浩特中考)一次函数y＝kx＋b满足kb＞0，且y随x的增大而减小，则此函数的图象不经过()A．第一象限B．第二象限C．第三象限D．第四象限5．(2018·济宁中考)在平面直角坐标系中，已知一次函数y＝－2x＋1的图象经过P1(x1，y1)，P2(x2，y2)两点，若x1＜x2，则y1y2.(填“＞”“＜”或“＝”)考点二确定一次函数的表达式(5年1考)命题角度❶待定系数法例3在直角坐标系中，一条直线经过A(－1，5)，P(－2，a)，B(3，－3)三点．(1)求a的值；(2)设这条直线与y轴相交于点D，求△OPD的面积．【分析】(1)根据A，B的坐标，利用待定系数法求出表达式，根据点P在直线上可求出a的值；(2)求出点D的坐标，再利用三角形面积公式解答即可．【自主解答】(1)设直线的表达式为y＝kx＋b.把A(－1，5)，B(3，－3)代入可得解得∴直线的表达式为y＝－2x＋3.∵点P(－2，a)在直线y＝－2x＋3上，∴－2×(－2)＋3＝a，即a＝7.(2)由(1)得，点P的坐标为(－2，7)，直线的表达式为y＝－2x＋3.令x＝0，则y＝3，∴直线与y轴的交点D的坐标为(0，3)，∴S△OPD＝×3×2＝3.用待定系数法求一次函数的表达式有两种情况：(1)已知两点坐标(或两组对应值)可列方程组求表达式；(2)已知b或k的值，只需一点坐标(或一组对应值)即可．特别地，一次函数发生平移时，平移前后k的值不发生变化．6．已知直线y＝－x＋8与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则直线AM的函数表达式是()A．y＝－x＋8B．y＝－x＋8C．y＝－x＋3D．y＝－x＋37．如图，过点A(2，0)的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB＝.(1)求点B的坐标；(2)若△ABC的面积为4，求直线l2的表达式．解：(1)∵点A(2，0)，AB＝，∴BO＝＝3，∴点B的坐标为(0，3)．(2)∵△ABC的面积为4，∴BC·AO＝4，即BC×2＝4，解得BC＝4.∵BO＝3，∴CO＝4－3＝1，∴C(0，－1)．设l2的表达式为y＝kx＋b，则∴直线l2的表达式为y＝x－1.命题角度❷图象的平移例4(2018·重庆中考A卷节选)如图，在平面直角坐标系中，直线y＝－x＋3过点A(5，m)且与y轴交于点B，把点A向左平移2个单位，再向上平移4个单位，得到点C.过点C且与y＝2x平行的直线交y轴于点D.求直线CD的表达式．【分析】先把A(5，m)代入y＝－x＋3得A(5，－2)，再利用点的平移规律得到C(3，2)，接着利用两直线平行的性质设CD的表达式为y＝2x＋b，然后把C点坐标代入求出b，即可得到直线CD的表达式．【自主解答】把A(5，m)代入y＝－x＋3得m＝－5＋3＝－2，则A(5，－2)．∵点A向左平移2个单位，再向上平移4个单位，得到点C，∴C(3，2)．∵过点C且与y＝2x平行的直线交y轴于点D，∴CD的表达式可设为y＝2x＋b，把C(3，2)代入得6＋b＝2，解得b＝－4，∴直线CD的表达式为y＝2x－4.混淆图象的平移规律一次函数图象的平移规律：左加右减自变量，上加下减常数项．此处需要注意的是，一次函数y＝kx＋b向左、向右平移n(n>0)个单位，得到y＝k(x±n)＋b，而不是y＝kx±n＋b.8．(2018·南充中考)直线y＝2x向下平移2个单位长度得到的直线是()A．y＝2(x＋2)B．y＝2(x－2)C．y＝2x－2D．y＝2x＋29．(2017·连云港中考)如图，在平面直