课件-全国-2019_（潍坊专版）2019中考数学复习 第1部分 第三章 函数 第七节 二次函数的综合应用课件.ppt

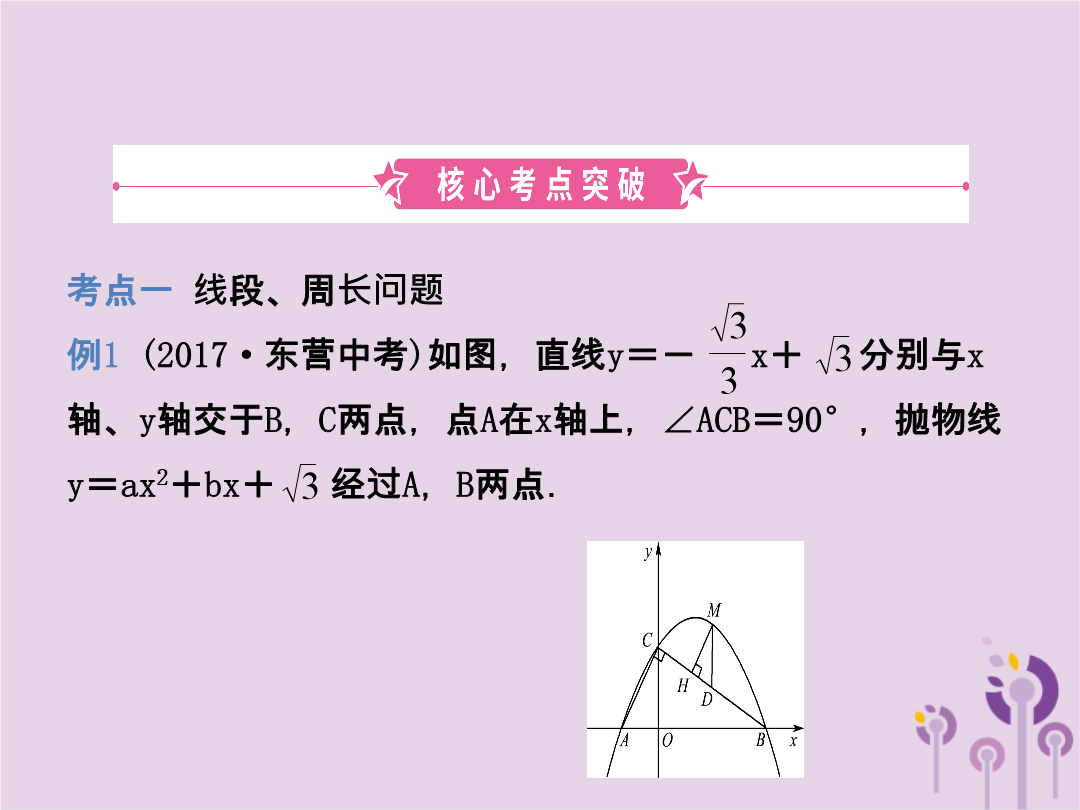
第七节二次函数的综合应用考点一线段、周长问题例1(2017·东营中考)如图，直线y＝－x＋分别与x轴、y轴交于B，C两点，点A在x轴上，∠ACB＝90°，抛物线y＝ax2＋bx＋经过A，B两点．(1)求A，B两点的坐标；(2)求抛物线的解析式；(3)点M是直线BC上方抛物线上的一点，过点M作MH⊥BC于点H，作MD∥y轴交BC于点D，求△DMH周长的最大值．【分析】(1)由直线解析式可求得B，C坐标，再利用相似三角形可求得OA，从而可求出A点坐标；(2)利用待定系数法可求得抛物线解析式；(3)根据题意可推出当MD取得最大值时，△DMH的周长最大，利用二次函数的性质得出最大值．【自主解答】(1)∵直线y＝－x＋分别与x轴、y轴交于B，C两点，∴点B的坐标为(3，0)，点C的坐标为(0，)．∵∠ACO＋∠BCO＝90°，∠ACO＋∠CAO＝90°，∴∠CAO＝∠BCO.∵∠AOC＝∠COB＝90°，∴△AOC∽△COB，∴∴AO＝1，∴点A的坐标为(－1，0)．(2)∵抛物线y＝ax2＋bx＋经过A，B两点，∴∴抛物线的解析式为y＝(3)由题意知，△DMH为直角三角形，且∠M＝30°，当MD取得最大值时，△DMH的周长最大．∴当x＝时，MD有最大值，∴△DMH周长的最大值为1．如图所示，二次函数的图象经过点D(0，)，且顶点C的横坐标为4，该图象在x轴上截得线段AB长为6.(1)利用二次函数的对称性直接写出点A，B的坐标．(2)求二次函数的解析式．(3)在该抛物线的对称轴上找一点P，使PA＋PD最小，求出点P的坐标．(4)在抛物线上是否存在点Q，使△QAB与△ABC相似？如果存在，求出点Q的坐标；如果不存在，请说明理由．解：(1)A(1，0)，B(7，0)．(2)设二次函数的解析式为y＝a(x－1)(x－7)．∵过点(0，)，∴代入得7a＝.解得a＝，∴二次函数的解析式为y＝(x－1)(x－7)．(3)∵点A，B关于直线x＝4对称，∴PA＝PB，PA＋PD＝PB＋PD≥DB，∴DB与对称轴的交点即为所求点P.如图，设直线x＝4与x轴交于点M.∵PM∥OD，∴∠BPM＝∠BDO.又∵∠PBM＝∠DBO，∴△BPM∽△BDO，∴∴PM＝∴点P的坐标为(4，)．(4)存在．由(2)可得出点C的坐标为(4，－)．∵AM＝3，∴在Rt△AMC中，tan∠ACM＝，∴∠ACM＝60°.∵AC＝BC，∴∠ACB＝120°.①如图所示，当点Q在x轴上方时，过点Q作QN⊥x轴于点N.如果AB＝BQ，由△ACB∽△ABQ得BQ＝6，∠ABQ＝∠ACB＝120°，则∠QBN＝60°，∴QN＝3，BN＝3，ON＝10，此时点Q的坐标为(10，3)．如果AB＝AQ，由对称性知Q的坐标为(－2，3)，经检验，点(10，3)与(－2，3)都在抛物线上．②当点Q在x轴下方时，△QAB就是△ACB，此时点Q的坐标是(4，－)．综上所述，存在这样的点Q，使△QAB与△ABC相似，点Q的坐标为(10，3)或(－2，3)或(4，－)．考点二图形面积问题例2(2017·潍坊中考)如图，抛物线y＝ax2＋bx＋c经过平行四边形ABCD的顶点A(0，3)，B(－1，0)，D(2，3)，抛物线与x轴的另一交点为E.经过点E的直线l将平行四边形ABCD分割为面积相等的两部分，与抛物线交于另一点F.点P为直线l上方抛物线上一动点，设点P的横坐标为t.(1)求抛物线的表达式；(2)当t为何值时，△PFE的面积最大？并求最大值的立方根；(3)是否存在点P使△PAE为直角三角形？若存在，求出t的值；若不存在，说明理由．【分析】(1)由A，B，D三点的坐标，利用待定系数法可求得抛物线的表达式；(2)由题意知l必过平行四边形ABCD的对称中心，由抛物线的对称性可求得E点坐标，从而可求得直线l的表达式，作PH⊥x轴，交直线l于点M，作FN⊥PH，则可用t表示出PM的长，从而可表示出△PEF的面积，再利用二次函数的性质可求得其最大值，再求其最大值的立方根即可；(3)由题意可知有∠PAE＝90°或∠APE＝90°两种情况，分别求得t的值即可．【自主解答】(1)将点A(0，3)，B(－1，0)，D(2，3)代入y＝ax2＋bx＋c得∴抛物线的表达式为y＝－x2＋2x＋3.(2)∵直线l将平行四边形ABCD分割为面积相等的两部分，∴l必过其对称中心(，)．由点A，D知，对称轴为x＝1，∴E(3，0)，设直线l的表达式为y＝kx＋m，代入点(，)和(3，0)得∴直线l的表达式为y＝－x＋.由解得xF＝－.如图，作PH⊥x轴，交l于点M，作FN⊥PH.点P的纵坐标为yP＝－t2＋2t＋3，点M的纵坐标为yM＝－t＋.∴PM＝yP－yM＝－t2＋2t＋3＋t－＝－t2＋t＋.则S△PFE＝S△PFM＋S△P