内容提供者
《微积分基本定理》(新人教选修2-2).省公开课一等奖全国示范课微课金奖PPT课件.pptx
2024-02-02
11金币
234KB
11页
胜利****实阿
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
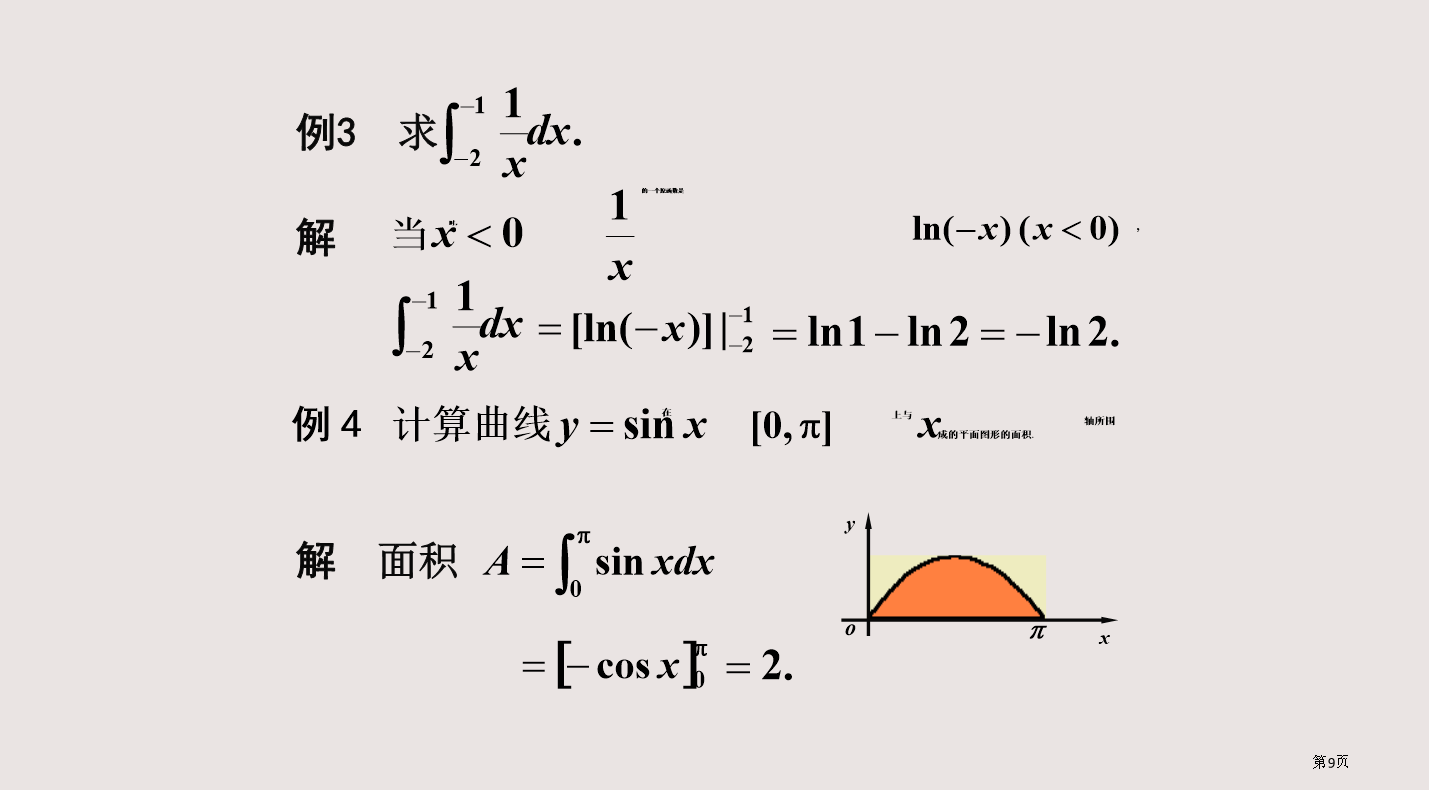
亲，该文档总共11页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
《微积分基本定理》(新人教选修2-2).省公开课一等奖全国示范课微课金奖PPT课件.pptx
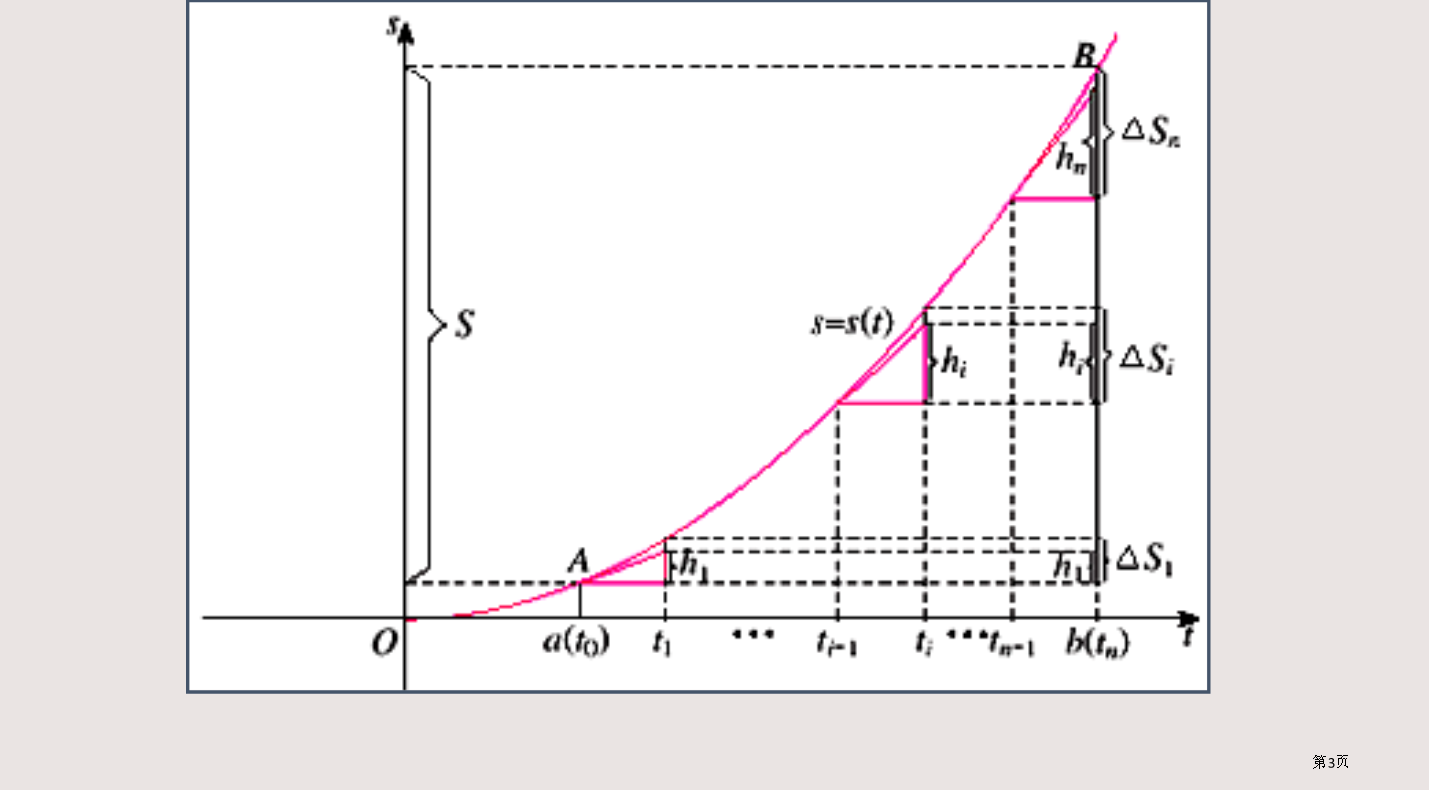
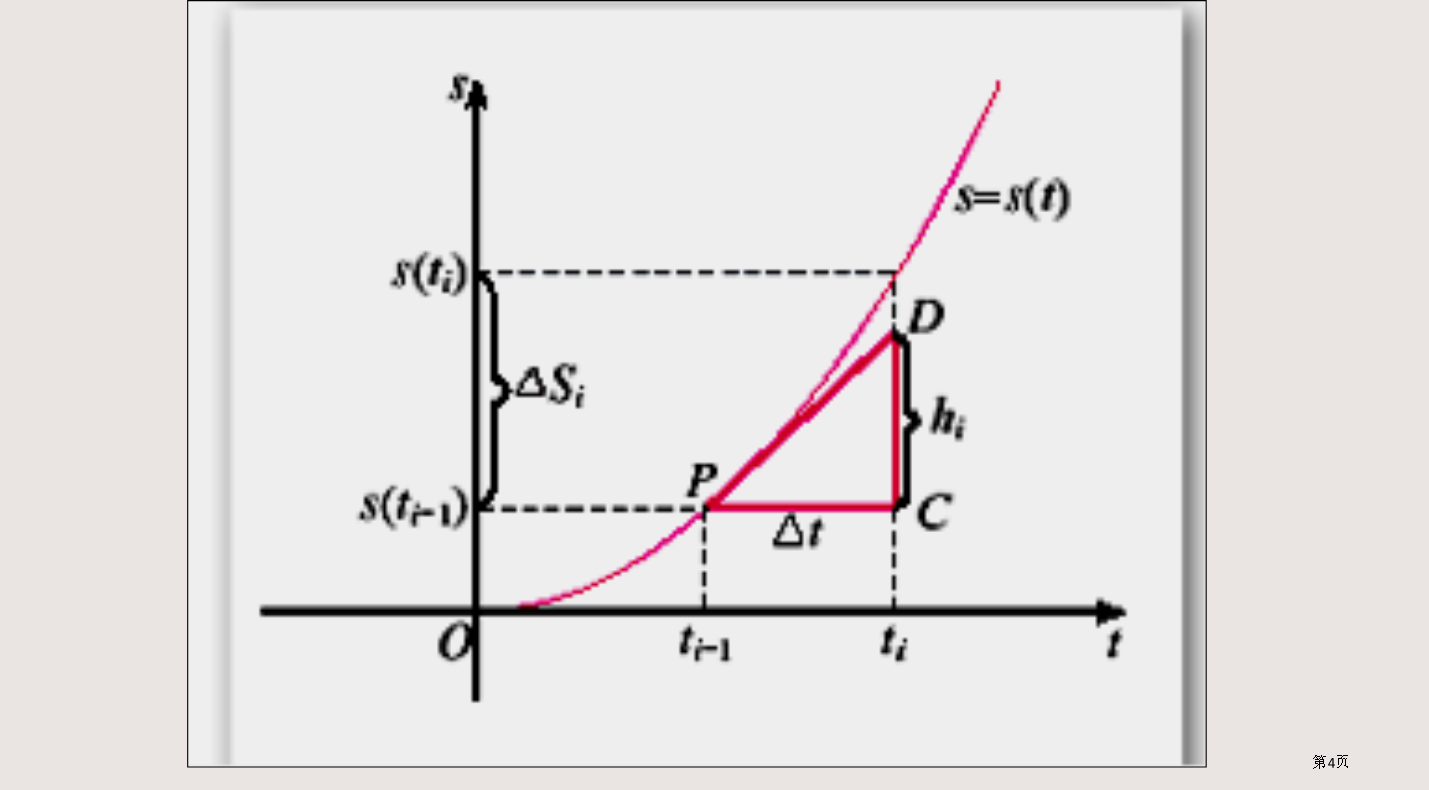
微积分基本定理变速直线运动中位移函数与速度函数联络物体位移是函数在两个端点处函数值之差，即从几何意义上看，由导数几何意义知求和得近似值取极限，由定积分定义得进而得出微积分基本定理定理（微积分基本定理）微积分基本定理表明：例1求例3求练习:1.求1、；2、4
2024-02-02
11
234KB
《微积分基本定理》(新人教选修2-2)省公开课一等奖全国示范课微课金奖PPT课件.pptx
微积分基本定理变速直线运动中位移函数与速度函数联络物体位移是函数在两个端点处函数值之差，即从几何意义上看，由导数几何意义知求和得近似值取极限，由定积分定义得进而得出微积分基本定理定理（微积分基本定理）微积分基本定理表明：例1求例3求练习:1.求1、；2、4
2024-10-16
10
234KB
162微积分基本定理省公开课一等奖全国示范课微课金奖PPT课件.pptx
1.6.2微积分基本定理定理（微积分基本定理）惯用积分公式例1求例3设,求.4作业：P62A组：1(2)(4)B组：1(2)(3)
2024-10-16
10
276KB
微积分-中值定理省公开课一等奖全国示范课微课金奖PPT课件.pptx
第三章中值定理与导数应用第三章中值定理与导数应用我们先经过几何图形直观了解罗尔定理:怎样证实？证由极限不等式性质知:注：(1)罗尔定理三个条件是充分条件，只要三个条件满足，就确保结论成立，若定理中三个条件缺乏其中任何一个，定理结论不一定成立.以下列图:解：注意与零点定理应用区分解：例3设为n次多项式，没有实根，试证实最多证：罗尔(1652-1719)是法国数学家.1652年4月21日生于昂贝尔特,1719年11月8日卒于巴黎.罗尔在数学上成就主要是在代数方面,专长于丢番图方程研究.罗尔于1691年在题为《
2024-10-17
10
429KB
一元微积分A：中值定理省公开课一等奖全国示范课微课金奖PPT课件.pptx
一、罗尔(Rolle)定理几何解释:证注意:若罗尔定理三个条件中有一个不满足,其结论可能不成立.例1例2.不用求出函数导数，判别方程根个数。例3.证实方程最少有一个小于1正根。二、拉格朗日中值定理证实：作辅助函数例4例5.证实：例6.证实：当时，例4三、柯西(Cauchy)中值定理几何解释:例5四、小结思索题思索题思索题解答练习题练习题答案
2024-10-16
10
457KB