微积分-中值定理省公开课一等奖全国示范课微课金奖PPT课件-豆柴文库

微积分-中值定理省公开课一等奖全国示范课微课金奖PPT课件.pptx

2024-10-17

10金币

429KB

20页

lj****88

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共20页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

微积分-中值定理省公开课一等奖全国示范课微课金奖PPT课件.pptx

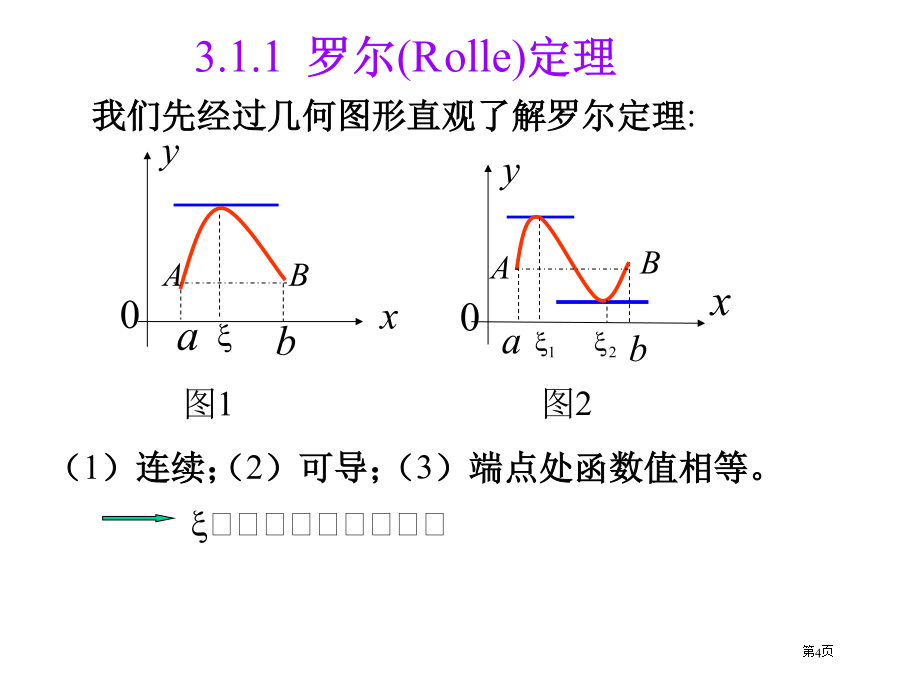
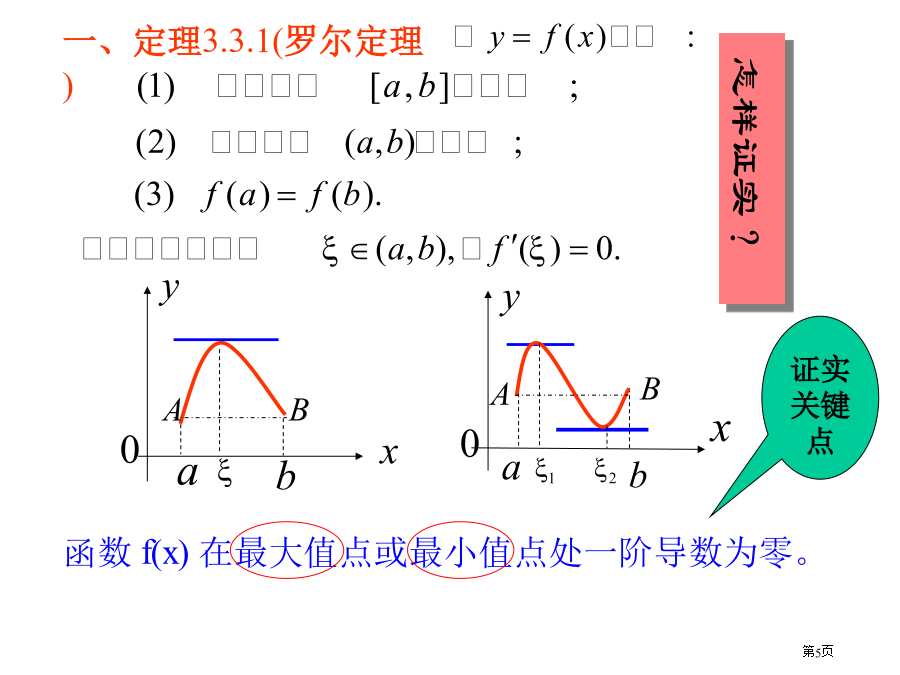
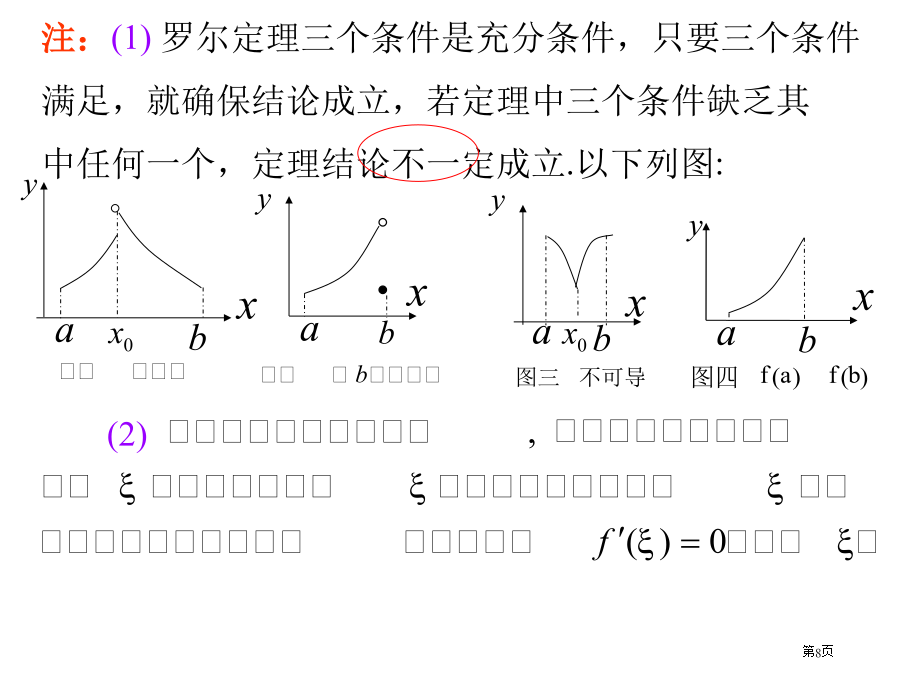
第三章中值定理与导数应用第三章中值定理与导数应用我们先经过几何图形直观了解罗尔定理:怎样证实？证由极限不等式性质知:注：(1)罗尔定理三个条件是充分条件，只要三个条件满足，就确保结论成立，若定理中三个条件缺乏其中任何一个，定理结论不一定成立.以下列图:解：注意与零点定理应用区分解：例3设为n次多项式，没有实根，试证实最多证：罗尔(1652-1719)是法国数学家.1652年4月21日生于昂贝尔特,1719年11月8日卒于巴黎.罗尔在数学上成就主要是在代数方面,专长于丢番图方程研究.罗尔于1691年在题为《

2024-10-17

429KB

一元微积分A：中值定理省公开课一等奖全国示范课微课金奖PPT课件.pptx

一、罗尔(Rolle)定理几何解释:证注意:若罗尔定理三个条件中有一个不满足,其结论可能不成立.例1例2.不用求出函数导数，判别方程根个数。例3.证实方程最少有一个小于1正根。二、拉格朗日中值定理证实：作辅助函数例4例5.证实：例6.证实：当时，例4三、柯西(Cauchy)中值定理几何解释:例5四、小结思索题思索题思索题解答练习题练习题答案

2024-10-16

457KB

高数(微积分)中值定理和导数应用省公开课一等奖全国示范课微课金奖PPT课件.pptx

第三章中值定理与导数应用中值定理微分中值定理包含：罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和柯西(Cauchy)中值定理一、费尔马(Fermat)引理（2）费尔马(Fermat)引理(极值必要条件)怎样证实罗尔定理？证实:三、拉格朗日(Lagrange)定理怎样证实拉格朗日定理？证实：拉格朗日公式各种形式推论1：推论2：四、柯西(Cauchy)定理证实：例1.设函数f(x)=(x1)(x2)(x3),试判断方程f'x有几个实根,分别在何区间?例２.设f(x)=x2+x.在

2024-10-17

1.6MB

湖南大学微积分21第21讲泰勒中值定理省公开课一等奖全国示范课微课金奖PPT课件.pptx

第四章一元函数导数与微分第七节泰勒中值定理泰勒中值定理一.带皮亚诺余项泰勒公式带皮亚诺余项马克劳林公式由极限知识可知,此时应有该公式称为带皮亚诺余项二阶泰勒公式.该公式称为带皮亚诺余项三阶泰勒公式.仿照以上做法,继续进行下去,即可得到普通带皮亚诺余项n阶泰勒公式.则在该邻域内有带拉格朗日余项马克劳林公式设带拉格朗日余项一阶泰勒公式为设带拉格朗日余项二阶泰勒公式为仿照以上做法,继续进行下去,可得到普通带拉格朗日余项n阶泰勒公式.带皮亚诺余项泰勒公式则在该邻域内有e近似计算公式其中,其中,其中,其中,实际应用

2024-02-04

788KB

162微积分基本定理省公开课一等奖全国示范课微课金奖PPT课件.pptx

1.6.2微积分基本定理定理（微积分基本定理）惯用积分公式例1求例3设,求.4作业：P62A组：1(2)(4)B组：1(2)(3)

2024-10-16

276KB