
3.1回归分析的基本思想及其初步应用(一).ppt

胜利****实阿






亲,该文档总共27页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

3.1回归分析的基本思想及其初步应用(一).ppt
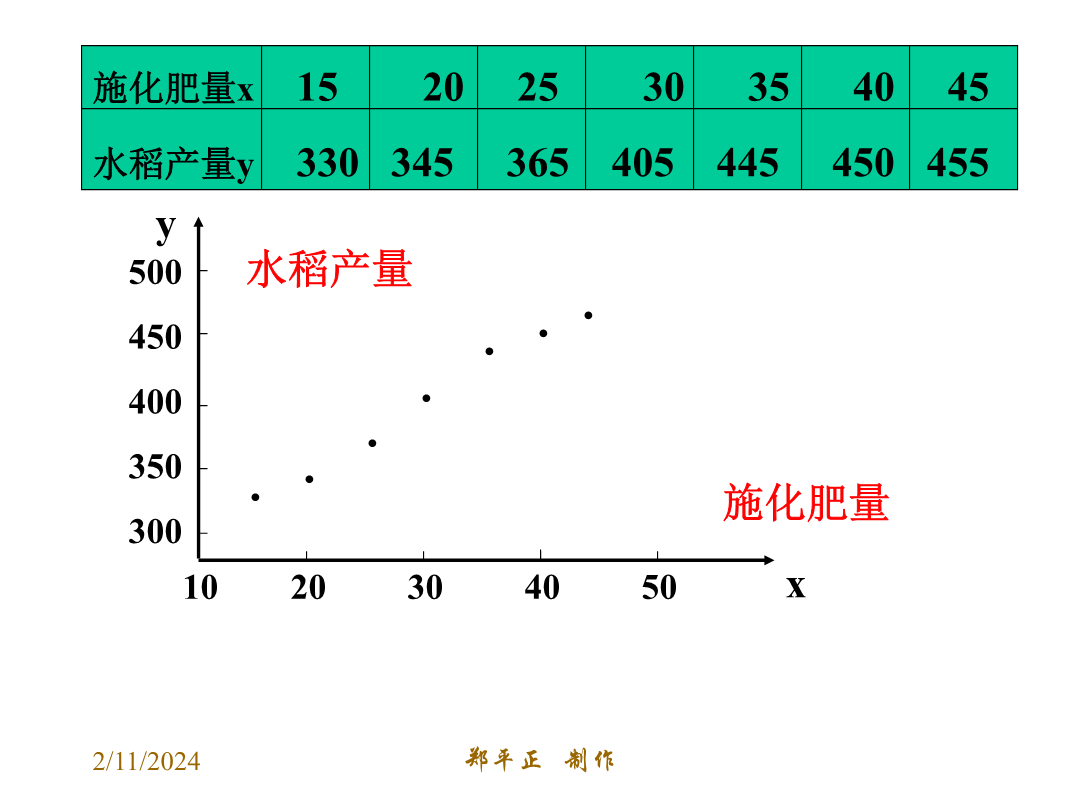
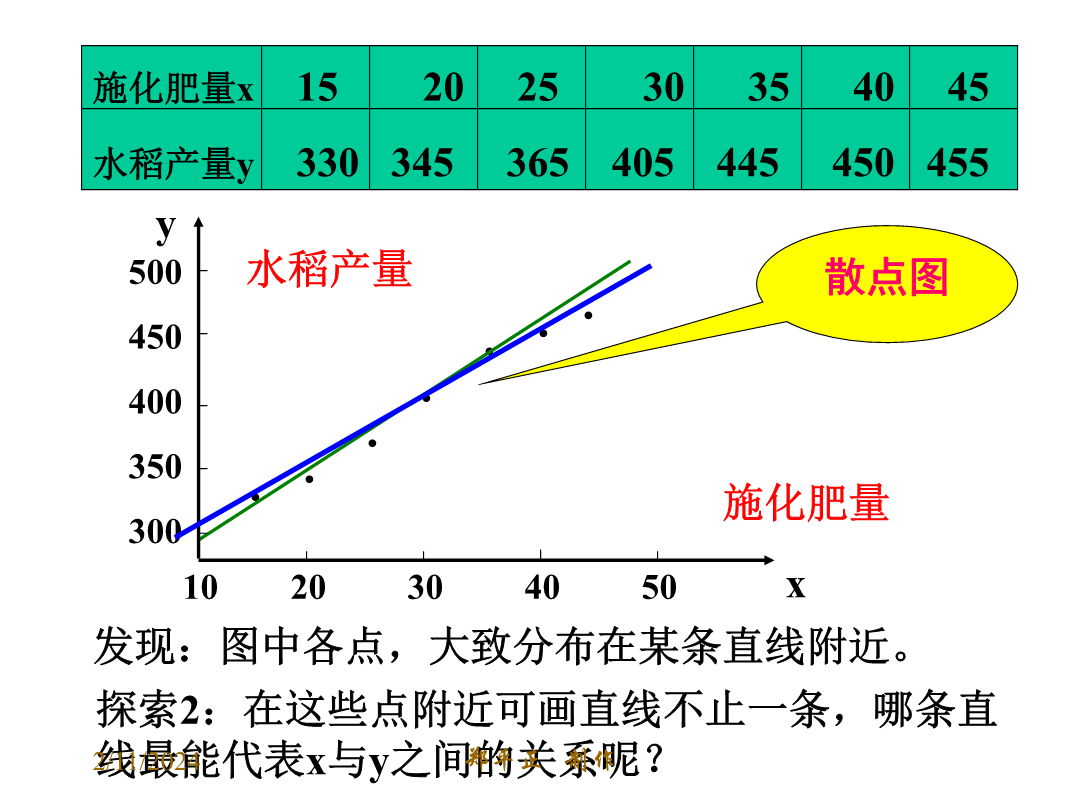
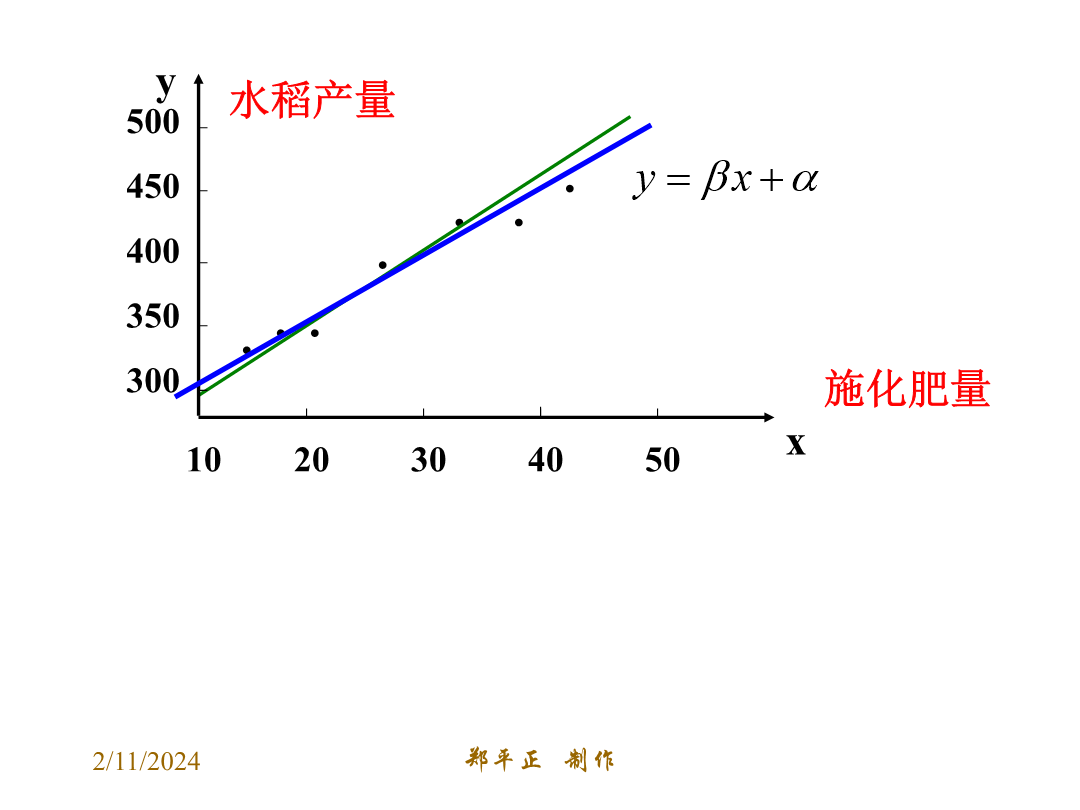
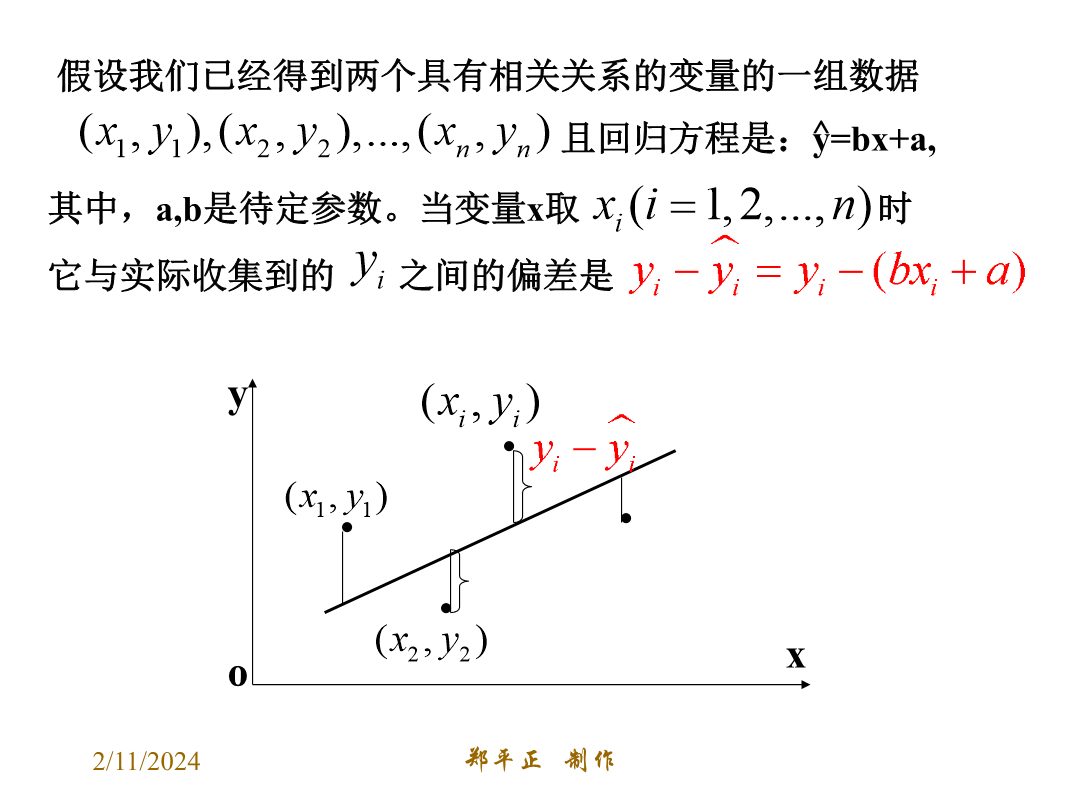
3.1回归分析的基本思想及其初步应用(一)数学3——统计内容画散点图了解最小二乘法的思想求回归直线方程y=bx+a用回归直线方程解决应用问题问题1:正方形的面积y与正方形的边长x之间的函数关系是1020304050自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。现实生活中存在着大量的相关关系。如:人的身高与年龄;产品的成本与生产数量;商品的销售额与广告费;家庭的支出与收入。等等10203040501020304050探究假设我们已经得到两个具有相关关系的变量的一组数据且回归方

3.1回归分析的基本思想及其初步应用(一).ppt
3.1回归分析的基本思想及其初步应用(一)数学3——统计内容画散点图了解最小二乘法的思想求回归直线方程y=bx+a用回归直线方程解决应用问题问题1:正方形的面积y与正方形的边长x之间的函数关系是1020304050自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。现实生活中存在着大量的相关关系。如:人的身高与年龄;产品的成本与生产数量;商品的销售额与广告费;家庭的支出与收入。等等10203040501020304050探究假设我们已经得到两个具有相关关系的变量的一组数据且回归方

3.1回归分析的基本思想及其初步应用.doc
第三章、统计案例3.1回归分析的基本思想及其初步应用(共计4课时)授课类型:新授课一、教学内容与教学对象分析学生将在必修课程学习统计的基础上,通过对典型案例的讨论,了解和使用一些常用的统计方法,进一步体会运用统计方法解决实际问题的基本思想,认识统计方法在决策中的作用。二、学习目标1、知识与技能通过本节的学习,了解回归分析的基本思想,会对两个变量进行回归分析,明确建立回归模型的基本步骤,并对具体问题进行回归分析,解决实际应用问题。2、过程与方法本节的学习,应该让学生通过实际问题去理解回归分析的必要性,明确回

3.1回归分析的基本思想及其初步应用.doc
第三章、统计案例3.1回归分析的基本思想及其初步应用(共计4课时)授课类型:新授课一、教学内容与教学对象分析学生将在必修课程学习统计的基础上,通过对典型案例的讨论,了解和使用一些常用的统计方法,进一步体会运用统计方法解决实际问题的基本思想,认识统计方法在决策中的作用。二、学习目标1、知识与技能通过本节的学习,了解回归分析的基本思想,会对两个变量进行回归分析,明确建立回归模型的基本步骤,并对具体问题进行回归分析,解决实际应用问题。2、过程与方法本节的学习,应该让学生通过实际问题去理解回归分析的必要性,明确回

《3.1回归分析的基本思想及其初步应用(一)》课件.ppt
3.1回归分析的基本思想及其初步应用(一)2024/10/4自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系.现实生活中存在着大量的相关关系.如:人的身高与年龄;产品的成本与生产数量;商品的销售额与广告费;家庭的支出与收入.等等数学3——统计内容画散点图了解最小二乘法的思想求回归直线方程y=bx+a用回归直线方程解决应用问题10203040502024/10/41020304050探究假设我们已经得到两个具有相关关系的变量的一组数据且回归方程是:y=bx+a,易知,截距和斜率分
