SPSS做回归分析PPT课件.ppt

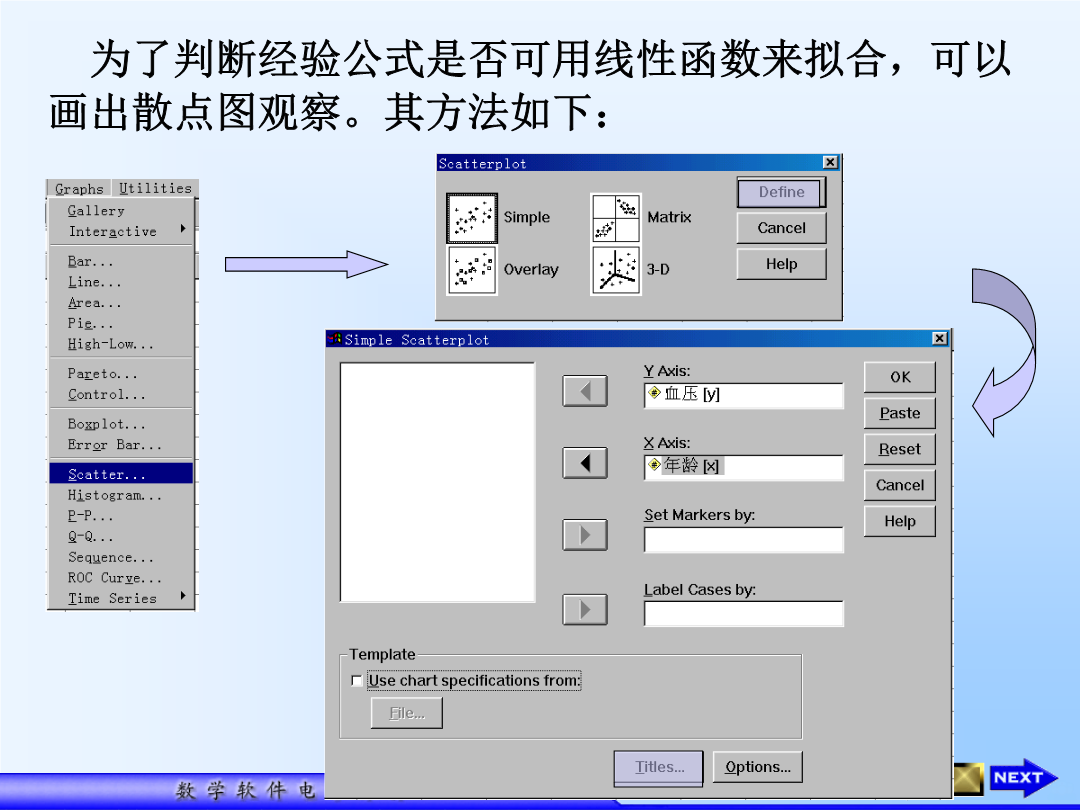
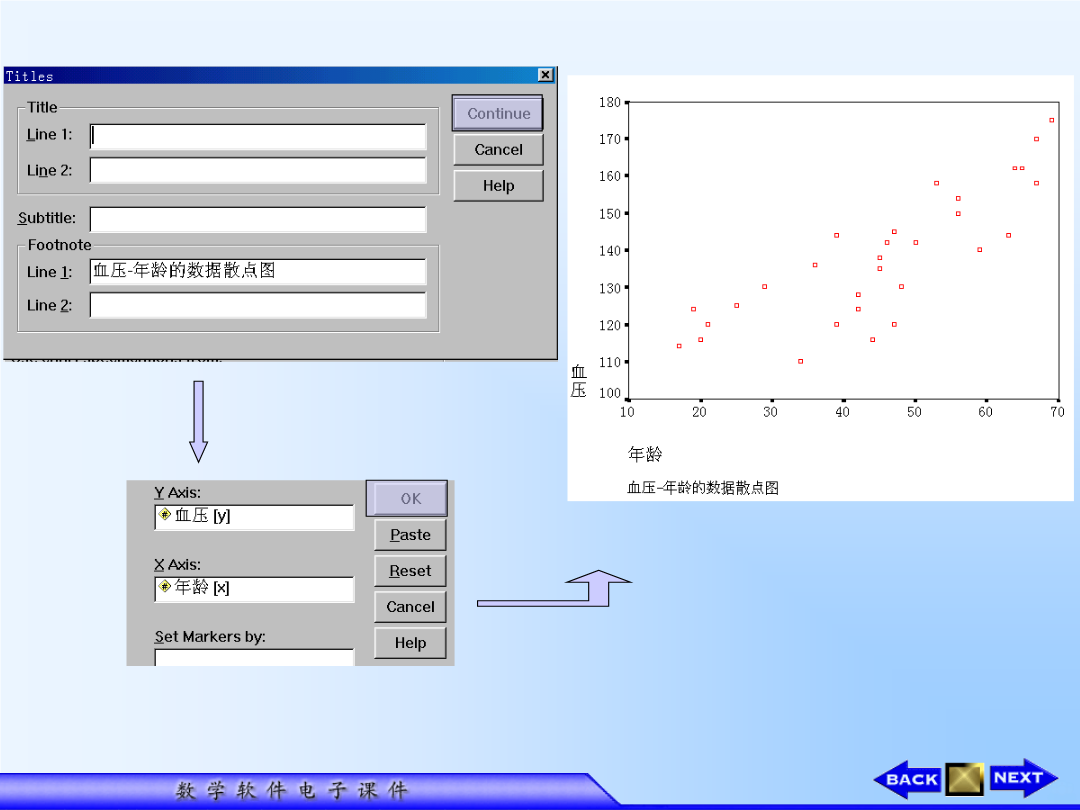
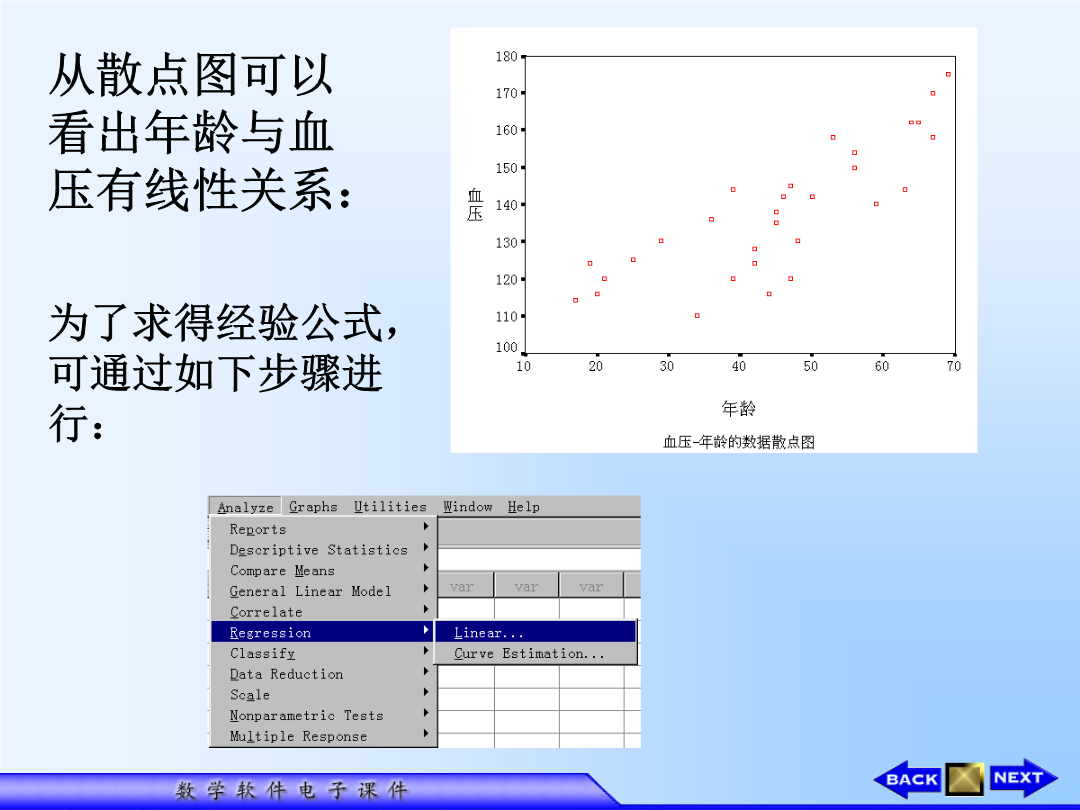
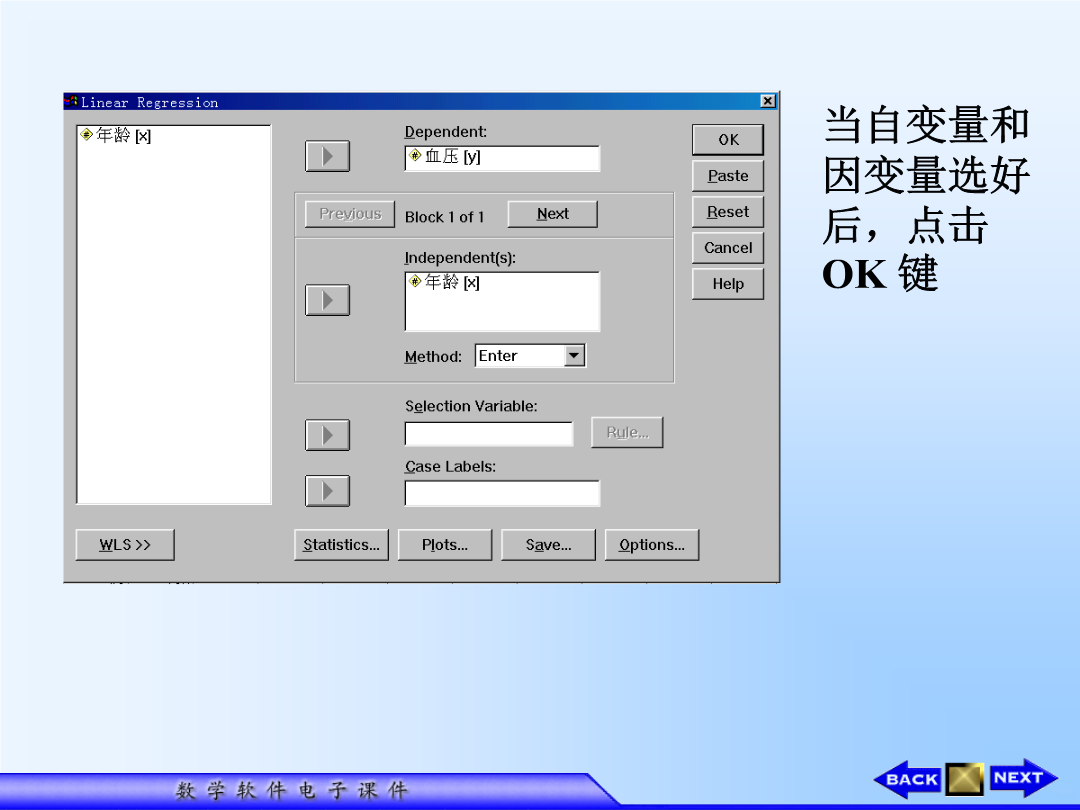
3.4用SPSS作回归分析一、简介以年龄为自变量x，血压为因变量y，可作出如下散点图：为了求得经验公式，可通过如下步骤进行：当自变量和因变量选好后，点击OK键Model为回归方程模型编号(不同方法对应不同模型)R为回归方程的复相关系数RSquare即R2系数，用以判断自变量对因变量的影响有多大，但这并不意味着越大越好——自变量增多时，R2系数会增大，但模型的拟合度未必更好AdjustedRSquare即修正R2，为了尽可能确切地反映模型的拟合度，用该参数修正R2系数偏差，它未必随变量个数的增加而增加Std.ErroroftheEstimate是估计的标准误差SumofSquares为回归平方和（Regression）、残差平方和（Residual）、总平方和（Total）df为自由度MeanSquareFSig为大于F的概率，其值为0.000，拒绝回归系数为0的原假设：b0=b1=0——即认为回归方程显著性成立Model为回归方程模型编号UnstandardizedCoefficients为非标准化系数，B为系数值，Std.Error为系数的标准差StandardizedCoefficients为标准化系数t为t检验，是偏回归系数为0(和常数项为0)的假设检验Sig.为偏回归系数为0(和常数项为0)的假设检验的显著性水平值B为Beta系数，Std.Error为相应的标准差第一导丝盘速度Y是合成纤维抽丝的重要因素，它与电流的周波X有密切关系，由生产记录得：检验说明线性关系显著对于多元线性回归主要需研究如下几个问题：方差分析的主要思想是把yi的总方差进行分解：如果自变量对Y的影响显著，则总方差主要应由xi引起，也就是原假设不成立，从而检验统计量为：在实际问题中，影响因变量Y的因素（自变量）可能很多。在回归方程中，如果漏掉了重要因素，则会产生大的偏差；但如果回归式中包含的因素太多，则不仅使用不便，且可能影响预测精度。如何选择适当的变量，建立最优的回归方程呢？开始2024/2/9某地区大春粮食产量y和大春粮食播种面积x1、化肥用量x2、肥猪发展头数x3、水稻抽穗扬花期降雨量x4的数据如下表，寻求大春粮食产量的预报模型。按Graphs→Scatter→Simple顺序展开对话框将y选入YAxis，然后将其余变量逐个选入XAxis，绘出散点图，观察是否适宜用线性方程来拟合。按Statistics→Regression→Linear顺序展开对话框将y作为因变量选入Dependent框中，然后将其余变量选入作为自变量选入Independent(s)框中被引入与被剔除的变量由复相关系数R=0.982说明该预报模型高度显著，可用于该地区大春粮食产量的短期预报方差分析表回归方程为：在汽油中加入两种化学添加剂，观察它们对汽车消耗1公升汽油所行里程的影响，共进行9次试验，得到里程Y与两种添加剂用量X1、X2之间数据如下：检验说明线性关系显著在实际问题中，常会遇到变量之间关系不是线性的相关关系，而是某种曲线的非线性相关关系。此时首先要确定回归函数的类型，其原则是：测量13个样品中某种金属含量Y与该样品采集点距中心观测点的距离X，有如下观测值：首先绘出散点图：通过点击右键观看选择适当的类型：Logarithmic因此我们有理由怀疑，原来的数据可能有错误（一般是打印错误），再结合原数据分析发现，Y=110.62是比较合适的，更改后再求解例.《概率论与数理统计》P286例9.4.22024/2/9