函数极限与连续.ppt

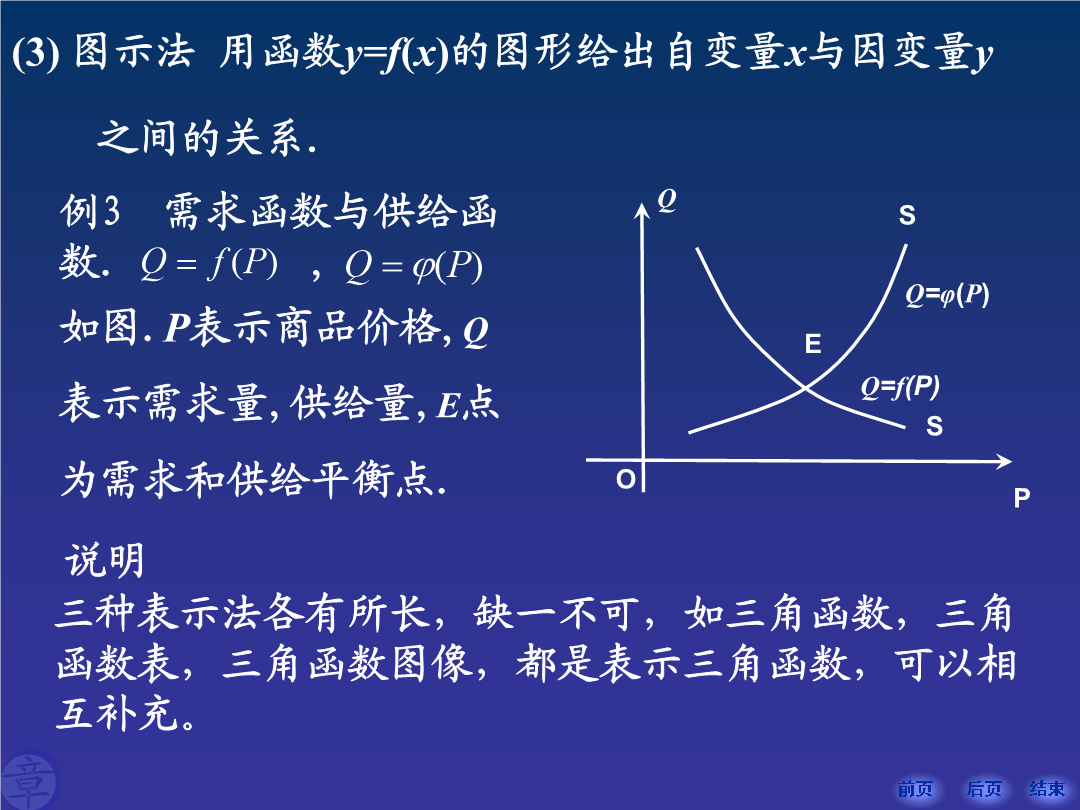
当自变量x取数值时，与对应的因变量y的值称为函数在点处的函数值,记为或.当x取遍D内的各个数值时,对应的变量y取值的全体组成1.1.2函数的表示法(3)图示法用函数y=f(x)的图形给出自变量x与因变量y例4求函数的定义域例5求函数的定义域.解当时,函数值在实际问题中,有时会遇到一个函数在定义域的不同范围内，用不同的解析式表示的情形，这样的函数称为分段函数．f(x)的定义域是[0,2]，定义设y是u的函数，y=f(u)，，而u是x的函数，并且的值域包含f(u)的定义域，即，则y通过u的联系也是x的函数，称此函数是由y=f(u)及复合而成的复合函数，记作例9求由函数组成的复合函数并求其定义域.(1)幂函数指数函数的定义域为.当a>1时，它严格单调增加；当0<a<1时，它严格单调减少.对于任何的a,的值域都是，函数的图形都过(0,1)点.在高等数学中，常用到以e为底的指数函数和以e为底的对数函数(记作lnx),lnx称为自然对数.这里e=2.7182818……，是一个无理数.数，并且在开区间内都是无界函数.(5)反三角函数2初等函数定义3设函数y=f(x)是定义在Df上的一个函数，其值域为Zf,对任意y∈Zf,如果有唯一确定的满足y=f(x)的x∈Df与之对应，则得到一个定义在Zf上以y为自变量的函数，我们称它为函数y=f(x)的反函数，记作例11设函数y=2x–3，求它的反函数并画出图形.1奇偶性例12讨论下列函数的奇偶性:设函数y=f(x),如果存在正常数T,使得对于定义域内的任何x均有f(x+T)=f(x)成立，则称函数y=f(x)为解设所求的周期为T，由于3单调性函数内是单调减少的，在区间上是单调增加的,而在区间内则不是单调函数.4有界性当函数y=f(x)在区间[a,b]上有界时，函数y=f(x)的图形恰好位于直线y=M和y=–Ｍ之间.应该注意，函数的有界性，不仅仅要注意函数的特点，还要注意自变量的变化范围Ｘ.1.1.7函数关系的建立总成本函数2总收益函数总收益是生产者出售一定量产品所得到的全部收入，是销售量的函数．设p为商品价格，为Q销售量，为总收益，则有例15已知某产品的总成本函数为求当生产100个该种产品时的总成本和平均成本．1数列的概念(1)2.数列的极限定义2如果当n无限地增大时，通项un无限地趋向于某个确定的常数a，则说当n趋于无穷大时，un以a为极限，记成单调增加或单调减少的数列统称为单调数列.对于数列，若存在正数M，使得对于一切的n都有1.当x→∞时,函数f(x)的极限当x→-∞时,函数f(x)无限趋近于常数1，此时我们称1为当x→-∞时函数f(x)的极限.2当x→x0时,函数f(x)的极限2在定义5中，x是以任意方式趋近于的，但在有些问题中，往往只需要考虑点x从的一侧趋近于时，函数f(x)的变化趋向．函数的极限与左、右极限有如下关系：定理4(唯一性定理)如果函数在某一变化过程中有极限，则其极限是唯一的．1.无穷小量定义7若变量Y在某过程下以零为极限，则称变量Y在此过程下为无穷小量，简称无穷小.例如函数时的无穷小，但当时不是无穷小。定理7在自变量的同一变化过程中(1)有限个无穷小的代数和仍为无穷小.例53.无穷大量4无穷小与无穷大的关系以后，遇到类似例6的题目，可直接写出结果.定理1设,则定理1中的(1)和(2)可以推广到有限个函数的代数和及乘积的极限情况.结论(2)还有如下常用的推论.一般地，设有多项式(有理整函数)例2式(1)与式(2)说明对于有理函数求关于的极限时，如果有理函数在点有定义，其极限值就是在点处的函数值，以后可以当做公式使用.例4例61.3.2两个重要极限当时有从而有例7这是重要极限2常用的另一种形式.例111.3.3无穷小的比较此时也称是比低阶的无穷小.所以当时,与x是等价无穷小,即关于等价无穷小在求极限中的应用，有如下定理.根据此定理，在求两个无穷小之比的极限时，若此极限不好求，可用分子、分母各自的等价无穷小来代替，如果选择适当，可简化运算.例15例17注意：相乘(除)的无穷小都可用各自的等价无穷小代换，但是相加(减)的无穷小的项不能作等价代换，例如1.4.1函数连续性的概念定义1：设函数在点的某邻域内有定义，当自变量在点处有增量时，相应的函数有增量,如果当自变量的增量趋于零时，函数的增量也趋于零，即则称函数在点处连续，点称为函数的连续点注：定义3：若函数满足，则称函数在点处左连续。同理可以定义右连续证明y=sinx在内连续1.4.2函数的间断点及其分类例22.跳跃间断点：当时，函数值不断地在两点之间跳动，左右极限均不存在间断点的类型：例6所以x=1是函数的可去间断点设函数y=f(u)在点处连续,u=f(x)在点处连续,且,则复合函数在点处连续.1.4.4闭区间上连续函数的性质定理5（