两个平面垂直的性质定理-豆柴文库

两个平面垂直的性质定理.ppt

2024-01-17

10金币

377KB

15页

胜利****实阿

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共15页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

两个平面垂直的性质定理.ppt

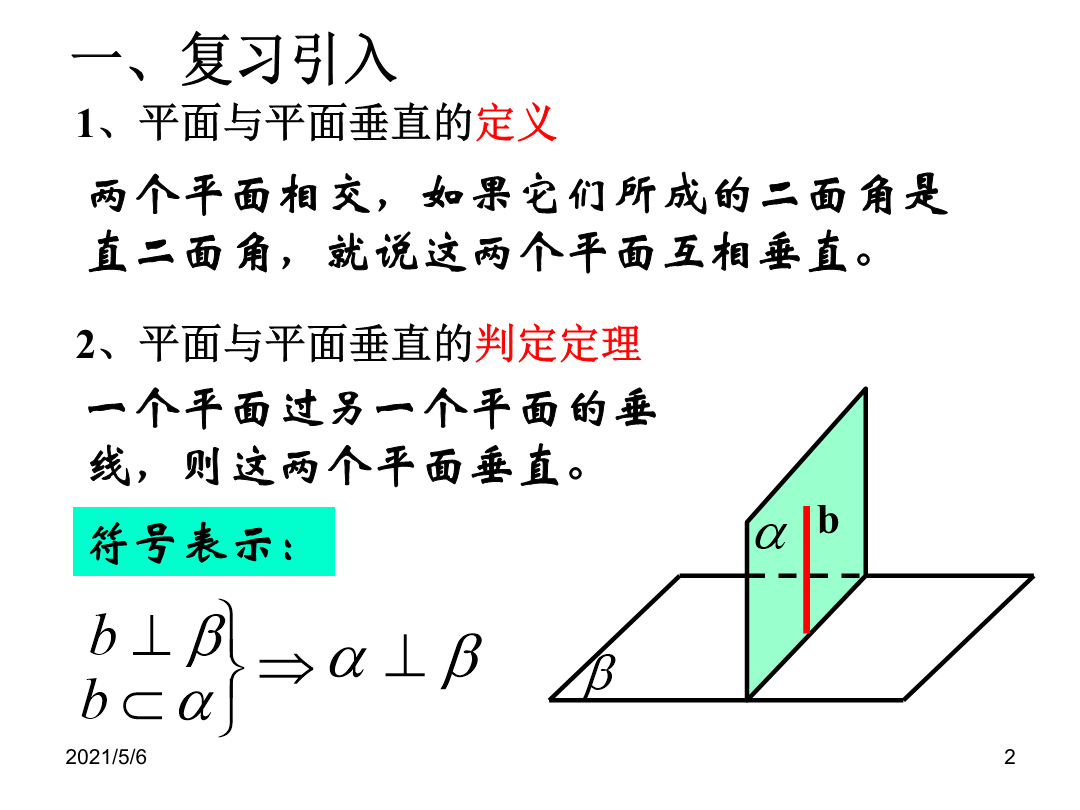
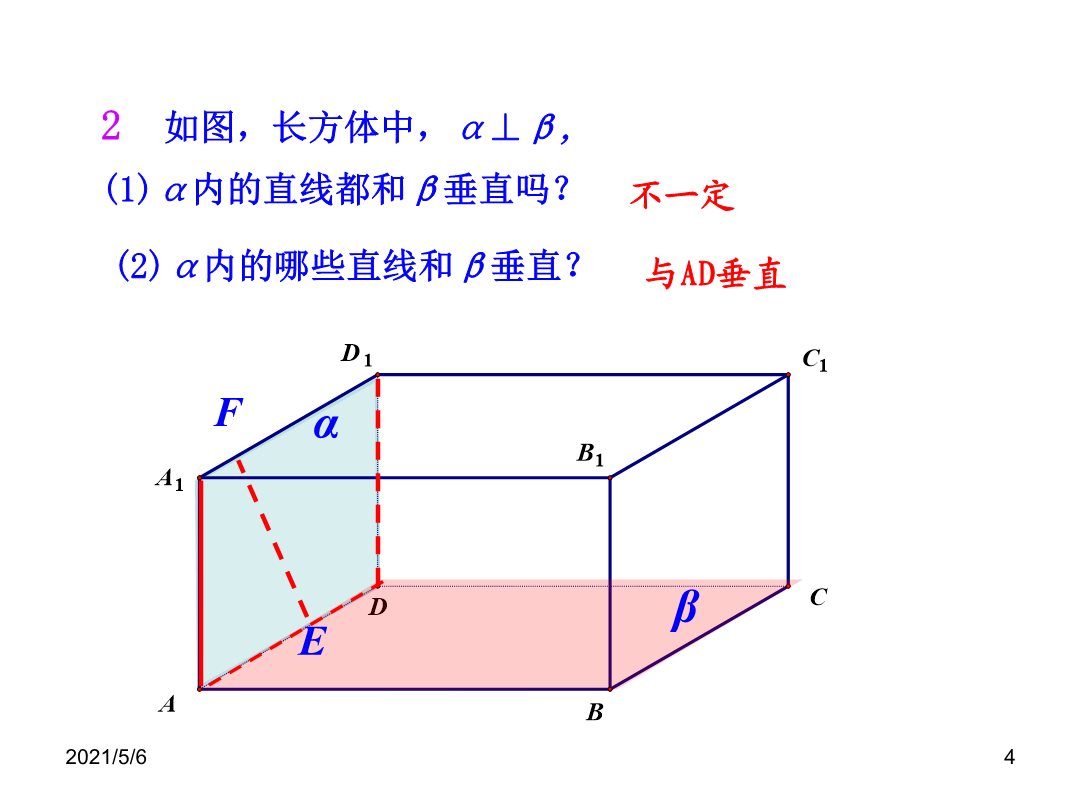
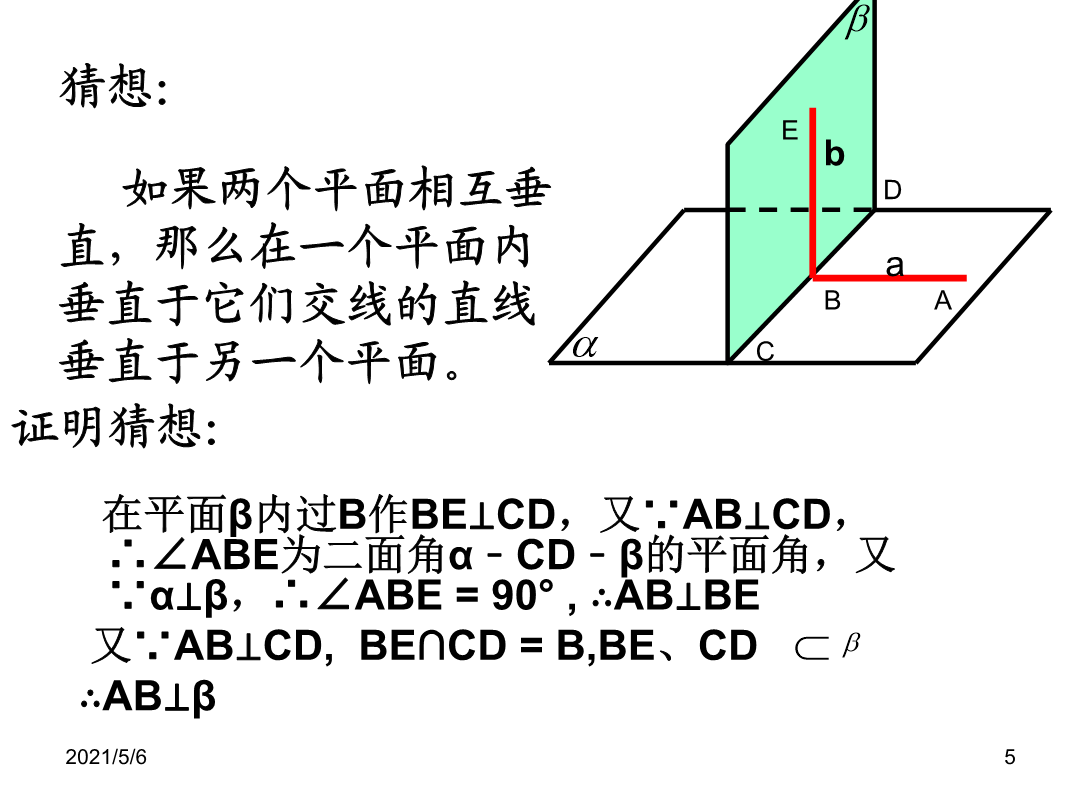
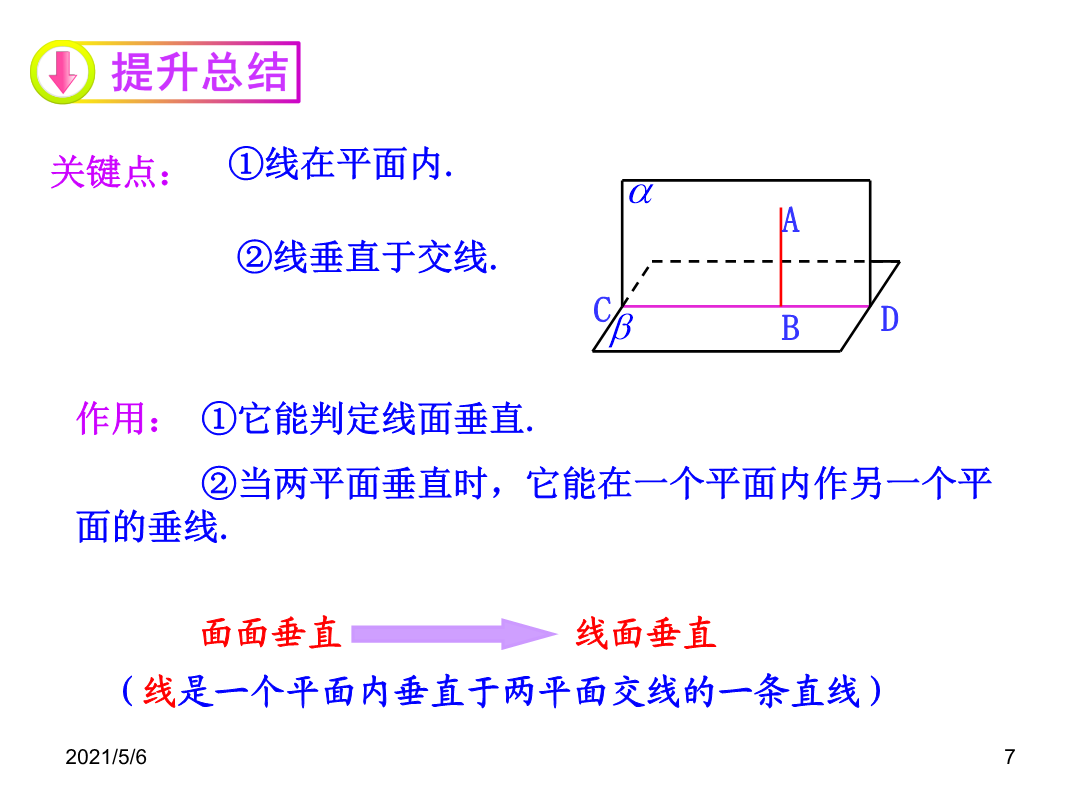
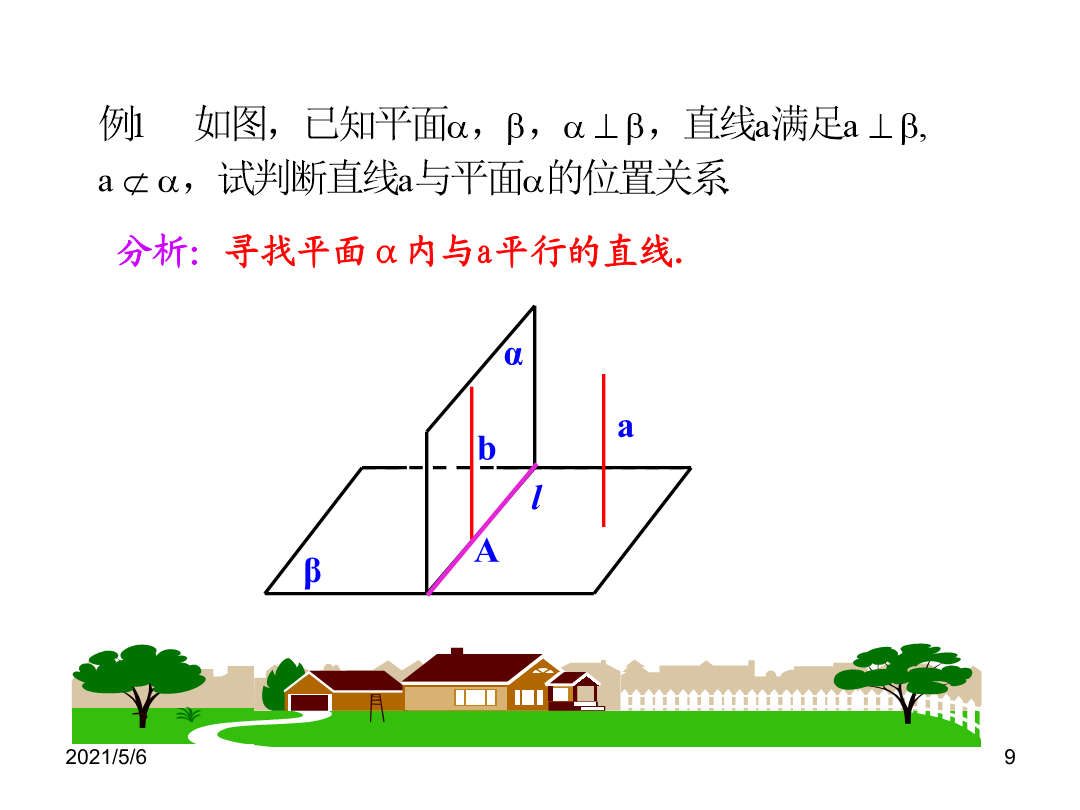
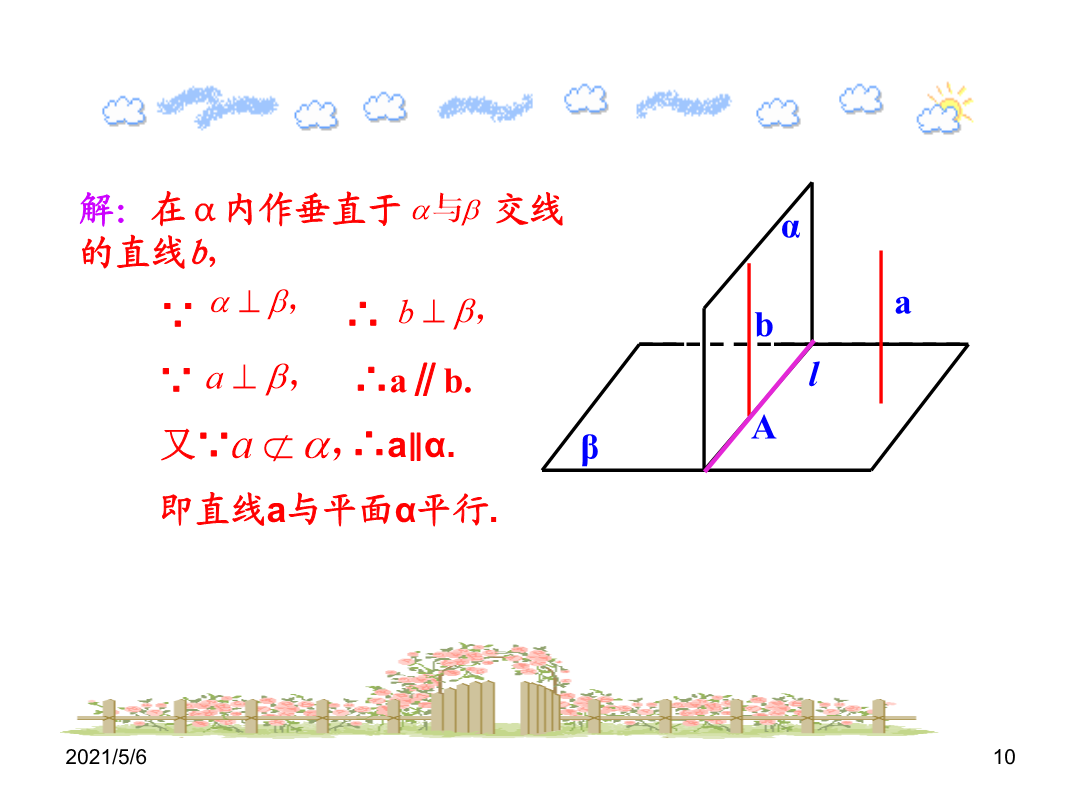
1.2.4平面与平面垂直的性质定理一、复习引入观察实验猜想：平面与平面垂直的性质定理（线是一个平面内垂直于两平面交线的一条直线）概念巩固α解：在α内作垂直于交线的直线b，∵∴∵∴a∥b.又∵∴a∥α.即直线a与平面α平行.α例2:求证：如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线必在第一个平面内．例3．S为三角形ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC。求证：AB⊥BC。证明：∵面PDC⊥底面ABCD，交线为DC，在正方形ABCD中，DC⊥CB，∴BC⊥平面

两个平面垂直的性质定理.ppt

1.2.4平面与平面垂直的性质定理一、复习引入观察实验猜想：平面与平面垂直的性质定理（线是一个平面内垂直于两平面交线的一条直线）概念巩固α解：在α内作垂直于交线的直线b，∵∴∵∴a∥b.又∵∴a∥α.即直线a与平面α平行.α例2:求证：如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线必在第一个平面内．例3．S为三角形ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC。求证：AB⊥BC。证明：∵面PDC⊥底面ABCD，交线为DC，在正方形ABCD中，DC⊥CB，∴BC⊥平面

两个平面垂直的性质定理(课堂PPT).ppt

1.2.4平面与平面垂直的性质定理一、复习引入观察实验猜想：平面与平面垂直的性质定理（线是一个平面内垂直于两平面交线的一条直线）概念巩固α解：在α内作垂直于交线的直线b，∵∴∵∴a∥b.又∵∴a∥α.即直线a与平面α平行.α例2:求证：如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线必在第一个平面内．例3．S为三角形ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC。求证：AB⊥BC。证明：∵面PDC⊥底面ABCD，交线为DC，在正方形ABCD中，DC⊥CB，∴BC⊥平面

两个平面垂直的性质定理ppt课件.ppt

1.2.4平面与平面垂直的性质定理一、复习引入观察实验猜想：平面与平面垂直的性质定理（线是一个平面内垂直于两平面交线的一条直线）概念巩固α解：在α内作垂直于交线的直线b，∵∴∵∴a∥b.又∵∴a∥α.即直线a与平面α平行.α例2:求证：如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线必在第一个平面内．例3．S为三角形ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC。求证：AB⊥BC。证明：∵面PDC⊥底面ABCD，交线为DC，在正方形ABCD中，DC⊥CB，∴BC⊥平面

两个平面垂直的性质定理ppt课件.ppt

1.2.4平面与平面垂直的性质定理一、复习引入观察实验猜想：平面与平面垂直的性质定理（线是一个平面内垂直于两平面交线的一条直线）概念巩固α解：在α内作垂直于交线的直线b，∵∴∵∴a∥b.又∵∴a∥α.即直线a与平面α平行.α例2:求证：如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线必在第一个平面内．例3．S为三角形ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC。求证：AB⊥BC。证明：∵面PDC⊥底面ABCD，交线为DC，在正方形ABCD中，DC⊥CB，∴BC⊥平面

收藏立即下载