
基于小波变换的脑电信号特征提取专家讲座.pptx

胜利****实阿









亲,该文档总共28页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

基于小波变换的脑电信号特征提取专家讲座.pptx
姓名:学号:一、EEG特点及普通处理流程一、脑电信号特点及普通处理流程一、脑电信号特点及普通处理流程普通处理流程:小波发展史:小波变换是近十几年新发展起来一个数学工具,是继一百多年前傅里叶(Fourier)分析之后又一个重大突破,它对不论是古老自然学科还是新兴高新应用技术学科均产生了强烈冲击。1909:AlfredHaar——发觉了Haar小波。1980:Morlet——Morlet小波,并分别与20世纪70年代提出了小波变换概念,20世纪80年代开发出了连续小波变换CWT(continuouswavel

基于小波变换的脑电信号特征提取.pptx
姓名:学号:一、EEG特点及一般处理流程一、脑电信号特点及一般处理流程一、脑电信号特点及一般处理流程一般处理流程:小波开展史:小波变换是近十几年新开展起来的一种数学工具,是继一百多年前的傅里叶(Fourier)分析之后的又一个重大突破,它对无论是古老的自然学科还是新兴的高新应用技术学科均产生了强烈的冲击。1909:AlfredHaar——发现了Haar小波。1980:Morlet——Morlet小波,并分别与20世纪70年代提出了小波变换的概念,20世纪80年代开发出了连续小波变换CWT〔continuo

基于小波变换的脑电信号特征提取.ppt
姓名(xìngmíng):学号:一、EEG特点及一般处理流程一、脑电信号特点及一般处理(chǔlǐ)流程一、脑电信号特点及一般(yībān)处理流程一般处理(chǔlǐ)流程:小波发展史:小波变换是近十几年新发展起来的一种数学工具,是继一百多年前的傅里叶(Fourier)分析之后的又一个重大突破,它对无论是古老的自然学科还是新兴的高新应用技术学科均产生了强烈的冲击。1909:AlfredHaar——发现了Haar小波。1980:Morlet——Morlet小波,并分别与20世纪70年代提出了小波变换的概念

基于小波变换的脑电信号特征提取.ppt
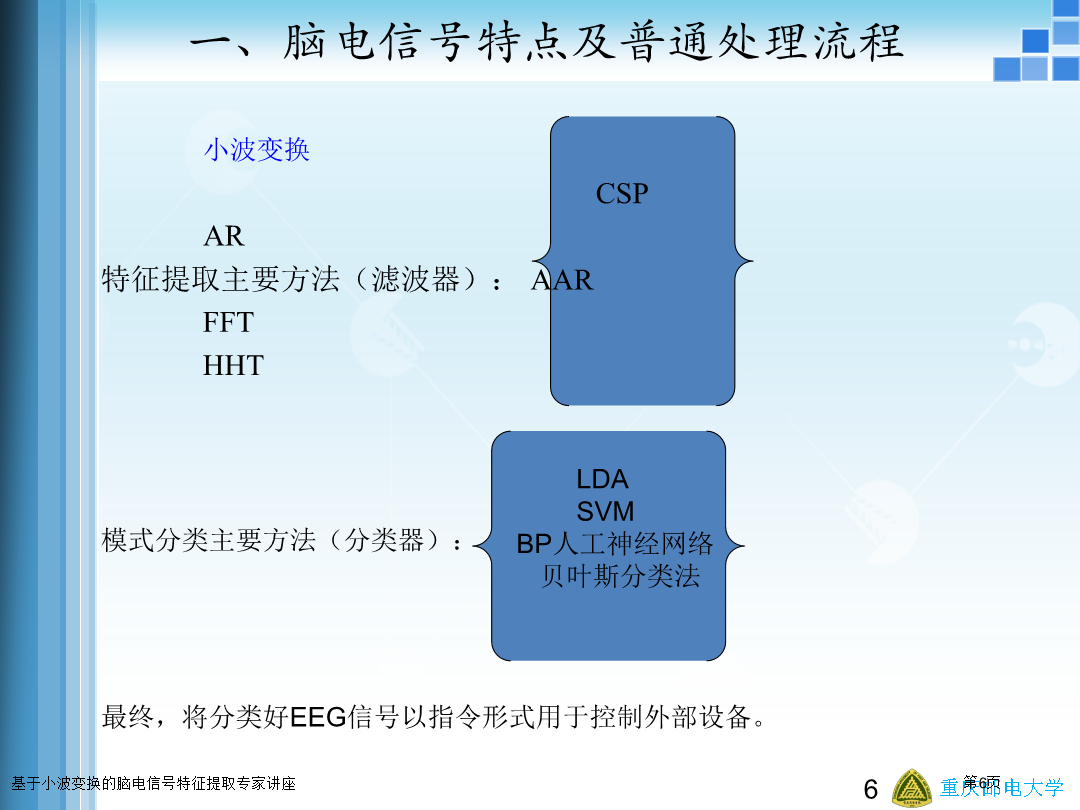
姓名:学号:一、EEG特点及一般处理流程一、脑电信号特点及一般处理流程一、脑电信号特点及一般处理流程一般处理流程:小波变换CSPAR特征提取的主要方法(滤波器):AARFFTHHT小波发展史:小波变换是近十几年新发展起来的一种数学工具,是继一百多年前的傅里叶(Fourier)分析之后的又一个重大突破,它对无论是古老的自然学科还是新兴的高新应用技术学科均产生了强烈的冲击。1909:AlfredHaar——发现了Haar小波。1980:Morlet——Morlet小波,并分别与20世纪70年代提出了小波变换的

基于小波变换的脑电信号特征提取.pptx
姓名:学号:一、EEG特点及一般处理流程一、脑电信号特点及一般处理流程一、脑电信号特点及一般处理流程一般处理流程:小波开展史:小波变换是近十几年新开展起来的一种数学工具,是继一百多年前的傅里叶(Fourier)分析之后的又一个重大突破,它对无论是古老的自然学科还是新兴的高新应用技术学科均产生了强烈的冲击。1909:AlfredHaar——发现了Haar小波。1980:Morlet——Morlet小波,并分别与20世纪70年代提出了小波变换的概念,20世纪80年代开发出了连续小波变换CWT〔continuo
